7.3.2.1 正弦函数、余弦函数的图象 教案
文档属性
| 名称 | 7.3.2.1 正弦函数、余弦函数的图象 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 257.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 07:31:58 | ||
图片预览


文档简介
第七章 三角函数
7.3.2.1 正弦函数、余弦函数的图象
由于三角函数是刻画周期变化现象的数学模型,这也是三角函数不同于其他类型函数的最重要的地方,而且对于周期函数,我们只要认识清楚它在一个周期的区间上的性质,那么它的性质也就完全清楚了,因此本节课利用单位圆中的三角函数的定义、三角函数值之间的内在联系性等来作图,从画出的图形中观察得出五个关键点,得到“五点法”画正弦函数、余弦函数的简图.
课程目标 学科素养
1.了解利用单位圆中的正弦线画正弦曲线的方法. 2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线. 3.理解正弦曲线与余弦曲线之间的联系. 1.数学抽象:正弦曲线与余弦曲线的概念; 2.逻辑推理:正弦曲线与余弦曲线的联系; 3.直观想象:正弦函数余弦函数的图像; 4.数学运算:五点作图; 5.数学建模:通过正弦、余弦图象图像,解决不等式问题及零点问题,这正是数形结合思想方法的应用.
重点:正弦函数、余弦函数的图象.
难点:正弦函数与余弦函数图象间的关系.
1.函数y=5sinx的最小正周期是________.
答案:5π
2.函数y=tan的最小正周期为________.
答案:
3.函数y=cos的最小正周期为________.
解析:T==π.
答案:π
4.已知函数f(x)=sin-1,则下列命题正确的是________.
①f(x)是最小正周期为1的函数;
②f(x)是最小正周期为2的函数;
③f(x)是最小正周期为的函数;
④f(x)是最小正周期为π的函数.
解析:f(x)=sin-1=-cos πx-1,
∴f(x)的最小正周期为T==2.
答案:②
知识点一 正弦函数、余弦函数的图象
思考1 课本上是利用什么来比较精确的画出正弦函数的图象的?其基本步骤是什么?
答案 利用正弦线,这种作图方法称为“几何法”,其基本步骤如下:
①作出单位圆:作平面直角坐标系,并在直角坐标系中y轴左侧的x轴上取一点O1,作出以O1为圆心的单位圆;
②等分单位圆,作正弦线:从⊙O1与x轴的交点A起,把⊙O1分成12等份.过⊙O1上各分点作x轴的垂线,得到对应于0,,,,…,2π等角的正弦线;
③找横坐标:把x轴上从0到2π这一段分成12等份;
④找纵坐标:把角x的正弦线向右平移,使它的起点与x轴上对应的点x重合,从而得到12条正弦线的12个终点;
⑤连线:用光滑的曲线将12个终点依次从左至右连接起来,即得到函数y=sin x,x∈[0,2π]的图象,如图.
因为终边相同的角有相同的三角函数值,所以函数y=sin x,x∈[2kπ,2(k+1)π),k∈Z且k≠0的图象与函数y=sin x,x∈[0,2π)的图象的形状完全一致.于是只要将函数y=sin x,x∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度),就可以得到正弦函数y=sin x,x∈R的图象,如图.
思考2 如何由正弦函数的图象通过图形变换得到余弦函数的图象?
答案 把y=sin x,x∈R的图象向左平移个单位长度,即可得到y=cos x,x∈R的图象.
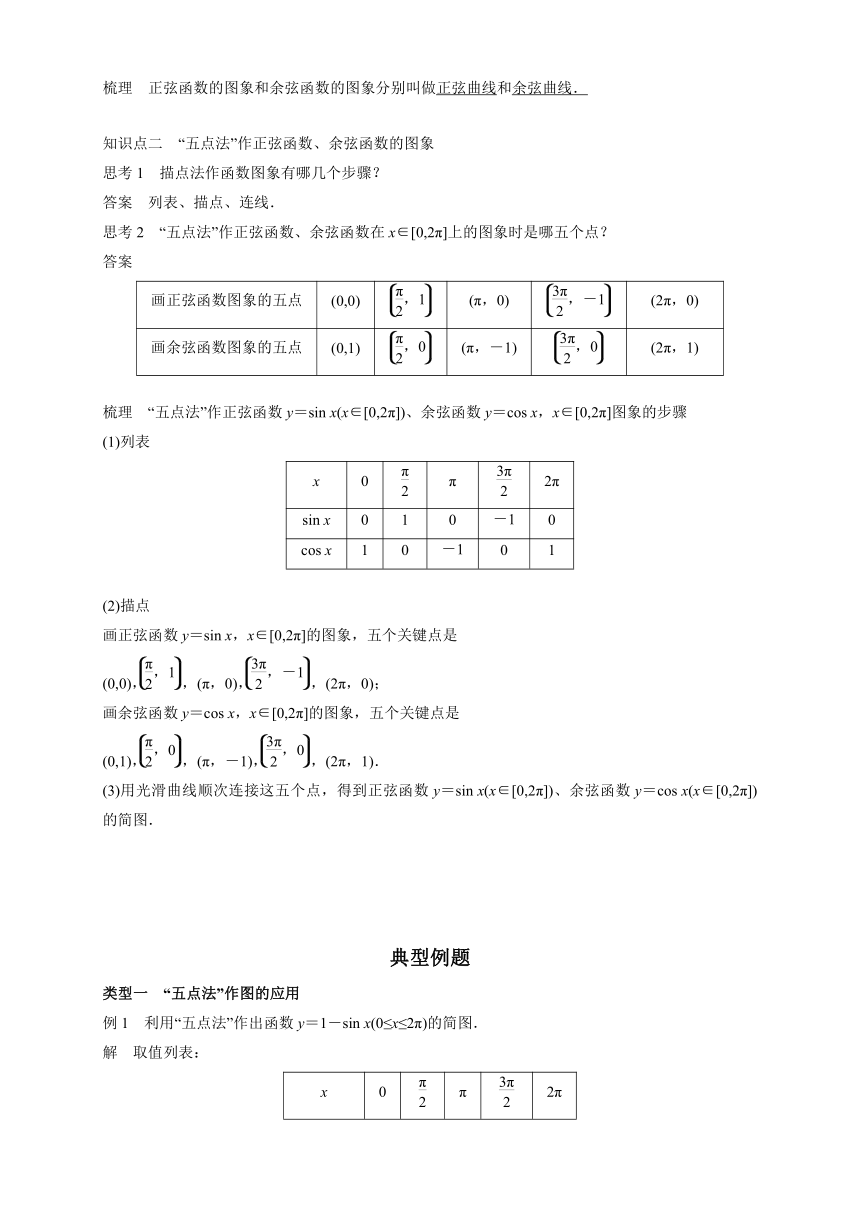
梳理 正弦函数的图象和余弦函数的图象分别叫做正弦曲线和余弦曲线.
知识点二 “五点法”作正弦函数、余弦函数的图象
思考1 描点法作函数图象有哪几个步骤?
答案 列表、描点、连线.
思考2 “五点法”作正弦函数、余弦函数在x∈[0,2π]上的图象时是哪五个点?
答案
画正弦函数图象的五点 (0,0) (π,0) (2π,0)
画余弦函数图象的五点 (0,1) (π,-1) (2π,1)
梳理 “五点法”作正弦函数y=sin x(x∈[0,2π])、余弦函数y=cos x,x∈[0,2π]图象的步骤
(1)列表
x 0 π 2π
sin x 0 1 0 -1 0
cos x 1 0 -1 0 1
(2)描点
画正弦函数y=sin x,x∈[0,2π]的图象,五个关键点是
(0,0),,(π,0),,(2π,0);
画余弦函数y=cos x,x∈[0,2π]的图象,五个关键点是
(0,1),,(π,-1),,(2π,1).
(3)用光滑曲线顺次连接这五个点,得到正弦函数y=sin x(x∈[0,2π])、余弦函数y=cos x(x∈[0,2π])的简图.
典型例题
类型一 “五点法”作图的应用
例1 利用“五点法”作出函数y=1-sin x(0≤x≤2π)的简图.
解 取值列表:
x 0 π 2π
sin x 0 1 0 -1 0
1-sin x 1 0 1 2 1
描点连线,如图所示.
总结 作正弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x的图象在[0,2π]内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.
跟踪训练1 (1)用“五点法”作出函数y=1-cos x(0≤x≤2π)的简图.
解 列表如下:
x 0 π 2π
cos x 1 0 -1 0 1
1-cos x 0 1 2 1 0
描点并用光滑的曲线连接起来,如图.
(2)(2017·长沙检测)利用正弦或余弦函数图象作出y=的图象.
解 由于y==|cos x|,因此只需作出y=|cos x|的图象即可,而y=|cos x|可由y=cos x将x轴下方的图象折到x轴上方,图象如下:
类型二 利用正、余弦函数图象解不等式
命题角度1 利用正、余弦函数图象解不等式
例2 利用正弦曲线,求满足解 首先作出y=sin x在[0,2π]上的图象,如图所示,作直线y=,根据特殊角的正弦值,可知该直线与y=sin x,x∈[0,2π]的交点横坐标为和.
作直线y=,该直线与y=sin x,x∈[0,2π]的交点横坐标为和.
观察图象可知,在[0,2π]上,当所以总结 用三角函数图象解三角不等式的方法
(1)作出相应正弦函数或余弦函数在[0,2π]上的图象;
(2)写出适合不等式在区间[0,2π]上的解集;
(3)根据公式一写出不等式的解集.
跟踪训练2 使不等式-2sin x≥0成立的x的取值集合是( )
A.
B.
C.
D.
答案 C
解析 不等式可化为sin x≤.
方法一 作图,正弦曲线及直线y=如图所示.
由图知,不等式的解集为.
方法二 如图所示,不等式的解集为.
命题角度2 利用正、余弦函数图象求定义域
例3 求函数f(x)=lg sin x+的定义域.
解 由题意,得x满足不等式组
即
作出y=sin x的图象,如图所示.
结合图象可得x∈[-4,-π)∪(0,π).
总结 一些三角函数的定义域可以借助函数图象直观地观察得到,同时要注意区间端点的取舍.
跟踪训练3 求函数y=的定义域.
解 为使函数有意义,需满足
即0由正弦函数的图象或单位圆(如图所示),
可得函数的定义域为.
本节课所画的图象较多,能迅速准确地画出函数图象对初学者来说是一个较高的要求,重在学生动手操作,不要怕学生出错.通过画图可以培养学生的动手能力、模仿能力.开始时要慢些,尤其是“五点法”,每个点都要能准确地找到,然后迅速画出图象.
7.3.2.1 正弦函数、余弦函数的图象
由于三角函数是刻画周期变化现象的数学模型,这也是三角函数不同于其他类型函数的最重要的地方,而且对于周期函数,我们只要认识清楚它在一个周期的区间上的性质,那么它的性质也就完全清楚了,因此本节课利用单位圆中的三角函数的定义、三角函数值之间的内在联系性等来作图,从画出的图形中观察得出五个关键点,得到“五点法”画正弦函数、余弦函数的简图.
课程目标 学科素养
1.了解利用单位圆中的正弦线画正弦曲线的方法. 2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线. 3.理解正弦曲线与余弦曲线之间的联系. 1.数学抽象:正弦曲线与余弦曲线的概念; 2.逻辑推理:正弦曲线与余弦曲线的联系; 3.直观想象:正弦函数余弦函数的图像; 4.数学运算:五点作图; 5.数学建模:通过正弦、余弦图象图像,解决不等式问题及零点问题,这正是数形结合思想方法的应用.
重点:正弦函数、余弦函数的图象.
难点:正弦函数与余弦函数图象间的关系.
1.函数y=5sinx的最小正周期是________.
答案:5π
2.函数y=tan的最小正周期为________.
答案:
3.函数y=cos的最小正周期为________.
解析:T==π.
答案:π
4.已知函数f(x)=sin-1,则下列命题正确的是________.
①f(x)是最小正周期为1的函数;
②f(x)是最小正周期为2的函数;
③f(x)是最小正周期为的函数;
④f(x)是最小正周期为π的函数.
解析:f(x)=sin-1=-cos πx-1,
∴f(x)的最小正周期为T==2.
答案:②
知识点一 正弦函数、余弦函数的图象
思考1 课本上是利用什么来比较精确的画出正弦函数的图象的?其基本步骤是什么?
答案 利用正弦线,这种作图方法称为“几何法”,其基本步骤如下:
①作出单位圆:作平面直角坐标系,并在直角坐标系中y轴左侧的x轴上取一点O1,作出以O1为圆心的单位圆;
②等分单位圆,作正弦线:从⊙O1与x轴的交点A起,把⊙O1分成12等份.过⊙O1上各分点作x轴的垂线,得到对应于0,,,,…,2π等角的正弦线;
③找横坐标:把x轴上从0到2π这一段分成12等份;
④找纵坐标:把角x的正弦线向右平移,使它的起点与x轴上对应的点x重合,从而得到12条正弦线的12个终点;
⑤连线:用光滑的曲线将12个终点依次从左至右连接起来,即得到函数y=sin x,x∈[0,2π]的图象,如图.
因为终边相同的角有相同的三角函数值,所以函数y=sin x,x∈[2kπ,2(k+1)π),k∈Z且k≠0的图象与函数y=sin x,x∈[0,2π)的图象的形状完全一致.于是只要将函数y=sin x,x∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度),就可以得到正弦函数y=sin x,x∈R的图象,如图.
思考2 如何由正弦函数的图象通过图形变换得到余弦函数的图象?
答案 把y=sin x,x∈R的图象向左平移个单位长度,即可得到y=cos x,x∈R的图象.
梳理 正弦函数的图象和余弦函数的图象分别叫做正弦曲线和余弦曲线.
知识点二 “五点法”作正弦函数、余弦函数的图象
思考1 描点法作函数图象有哪几个步骤?
答案 列表、描点、连线.
思考2 “五点法”作正弦函数、余弦函数在x∈[0,2π]上的图象时是哪五个点?
答案
画正弦函数图象的五点 (0,0) (π,0) (2π,0)
画余弦函数图象的五点 (0,1) (π,-1) (2π,1)
梳理 “五点法”作正弦函数y=sin x(x∈[0,2π])、余弦函数y=cos x,x∈[0,2π]图象的步骤
(1)列表
x 0 π 2π
sin x 0 1 0 -1 0
cos x 1 0 -1 0 1
(2)描点
画正弦函数y=sin x,x∈[0,2π]的图象,五个关键点是
(0,0),,(π,0),,(2π,0);
画余弦函数y=cos x,x∈[0,2π]的图象,五个关键点是
(0,1),,(π,-1),,(2π,1).
(3)用光滑曲线顺次连接这五个点,得到正弦函数y=sin x(x∈[0,2π])、余弦函数y=cos x(x∈[0,2π])的简图.
典型例题
类型一 “五点法”作图的应用
例1 利用“五点法”作出函数y=1-sin x(0≤x≤2π)的简图.
解 取值列表:
x 0 π 2π
sin x 0 1 0 -1 0
1-sin x 1 0 1 2 1
描点连线,如图所示.
总结 作正弦曲线要理解几何法作图,掌握五点法作图.“五点”即y=sin x或y=cos x的图象在[0,2π]内的最高点、最低点和与x轴的交点.“五点法”是作简图的常用方法.
跟踪训练1 (1)用“五点法”作出函数y=1-cos x(0≤x≤2π)的简图.
解 列表如下:
x 0 π 2π
cos x 1 0 -1 0 1
1-cos x 0 1 2 1 0
描点并用光滑的曲线连接起来,如图.
(2)(2017·长沙检测)利用正弦或余弦函数图象作出y=的图象.
解 由于y==|cos x|,因此只需作出y=|cos x|的图象即可,而y=|cos x|可由y=cos x将x轴下方的图象折到x轴上方,图象如下:
类型二 利用正、余弦函数图象解不等式
命题角度1 利用正、余弦函数图象解不等式
例2 利用正弦曲线,求满足
作直线y=,该直线与y=sin x,x∈[0,2π]的交点横坐标为和.
观察图象可知,在[0,2π]上,当
(1)作出相应正弦函数或余弦函数在[0,2π]上的图象;
(2)写出适合不等式在区间[0,2π]上的解集;
(3)根据公式一写出不等式的解集.
跟踪训练2 使不等式-2sin x≥0成立的x的取值集合是( )
A.
B.
C.
D.
答案 C
解析 不等式可化为sin x≤.
方法一 作图,正弦曲线及直线y=如图所示.
由图知,不等式的解集为.
方法二 如图所示,不等式的解集为.
命题角度2 利用正、余弦函数图象求定义域
例3 求函数f(x)=lg sin x+的定义域.
解 由题意,得x满足不等式组
即
作出y=sin x的图象,如图所示.
结合图象可得x∈[-4,-π)∪(0,π).
总结 一些三角函数的定义域可以借助函数图象直观地观察得到,同时要注意区间端点的取舍.
跟踪训练3 求函数y=的定义域.
解 为使函数有意义,需满足
即0
可得函数的定义域为.
本节课所画的图象较多,能迅速准确地画出函数图象对初学者来说是一个较高的要求,重在学生动手操作,不要怕学生出错.通过画图可以培养学生的动手能力、模仿能力.开始时要慢些,尤其是“五点法”,每个点都要能准确地找到,然后迅速画出图象.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
