2021-2022学年六年级下学期数学第六单元6.1.3式与方程(课件)(共17张PPT)
文档属性
| 名称 | 2021-2022学年六年级下学期数学第六单元6.1.3式与方程(课件)(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
式与方程
复习导入
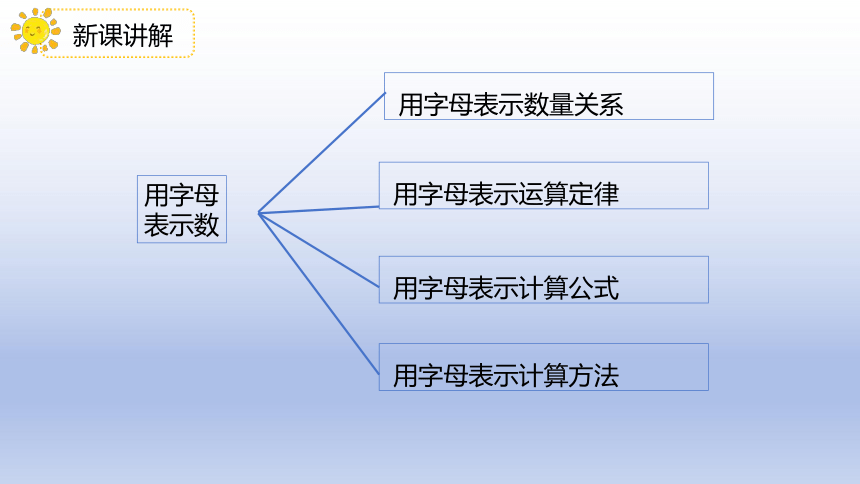
用字母表示数可以简明地表达数量、数量关系、运算定律和计算公式等,为研究和解决问题带来很多方便。
阅读教材第81页,自主整理复习。整理和复习时,我们可以根据学习的先后顺序系统地整理和复习,也可以借助教材提供的内容按边填写边回顾的方法进行整理复习。
用字母
表示数
用字母表示数量关系
用字母表示运算定律
用字母表示计算公式
用字母表示计算方法
新课讲解
知识梳理
1.填空。
①用s表示路程,v表示速度,t表示时间,那么s=( )。
②b乘5.6可以写作( ),还可以写作( );a乘h可以写作( ),还可以写作( )。
vt
5.6b
5.6·b
ah
a·h
一根绳子长48米,截成甲、乙两段,
其中,乙绳长度是甲绳的60%。
甲、乙两绳各长多少米?
总和关系
倍数关系
①多少分钟后,两人共折纸船40个?
(元元每分钟折纸船个数+路路每分钟折纸船个数)×时间=两人共折纸船个数
解:设 x 分钟后,两人共折纸船40个。
(5÷10+3÷10)x = 40
x = 50
答:50分钟后,两人共折纸船40个。
什么是方程的解?什么是解方程?怎样检验方程的解?
求方程的解的过程叫做解方程。
使方程左右两边相等的未知数的值叫做方程的解。
检验方程的解的方法:将未知数的值代入方程,看方程的左右两边是否相等。如果相等,所求的未知数的值就是方程的解,否则就不是。
体育室内足球的个数是篮球的75%,篮球比足球多6个。篮球和足球各有几个?
解:设篮球有X个,则足球有75%X个。
X-75%X=6
X=24
足球个数:75%X=75%×24=18个。
答:篮球有24个,足球有18个。
你会自己检验吗?
方程与等式的联系和区别
所有的方程都是等式,等式包括方程。
联系
所有的等式不一定是方程,等式范围更大;等式不一定含有未知数,方程必须含有未知数。
区别
新课讲解
两个粮库共存粮420 t,从甲粮库取出 的粮食到乙粮库,两个粮库的存粮就一样多了。原来甲粮库存粮多少吨?(先把线段图补充完整,再解答)[★★★★]
x
420-x
解:设原来甲粮库存粮 x t。
答:原来甲粮库存粮 270 t。
甲粮库存粮-甲粮库存粮× =乙粮库存粮+甲粮库存粮×
建筑工地上有一堆水泥,每天用a吨,用了5天,还剩下10吨。已经用去( )吨水泥,原来一共有( )吨水泥。
5a
5a+10
每天用a吨,5天就用了5个a吨,即a×5=5a(吨);用去的吨数加剩下的吨数就是原来一共有的吨数。
1.李奶奶家本月用电a千瓦时,比上个月多用10千瓦时,上个月用电
( )千瓦时。
2.如果每千瓦时电的价格是c元,李奶奶家本月的电费是( )元。
李奶奶家银行缴费卡上原有215元,扣除本月电费后,还剩( )元。
3.三个连续的自然数,最大的一个是n,那么最小的一个数是( )。
a-10
ac
215-ac
n-2
填一填。
课堂练习
(1)x=34是方程。 ( )
(2)a2一定比a3小。 ( )
√
判断。
×
(3)三个连续的自然数,最小的是a,这三个自然数的和是3a。 ( )
(4)如果n是自然数,那么2n+1一定是奇数。( )
(5)若b>a>0,则a的倒数比b的倒数大。 ( )
含有未知数的等式叫做方程。
当a=1或0时,a2=a3;当0<a<1时,a2>a3。
a+(a+1)+(a+2)=3a+3
2n一定是偶数,偶数加奇数一定等于奇数。
1
a
-和-比较大小,分子相同,分母越小,分数越大。
1
b
×
√
√
课堂小结
我的收获
等式的两边同时加上或减去同一个数(或式子),结果仍相等。
等式的两边同时乘或除以(0除外)
同一个数(或式子),结果仍相等。
课后作业
1、从教材课后习题中选取2、从课时练中选取
同学们再见
式与方程
复习导入
用字母表示数可以简明地表达数量、数量关系、运算定律和计算公式等,为研究和解决问题带来很多方便。
阅读教材第81页,自主整理复习。整理和复习时,我们可以根据学习的先后顺序系统地整理和复习,也可以借助教材提供的内容按边填写边回顾的方法进行整理复习。
用字母
表示数
用字母表示数量关系
用字母表示运算定律
用字母表示计算公式
用字母表示计算方法
新课讲解
知识梳理
1.填空。
①用s表示路程,v表示速度,t表示时间,那么s=( )。
②b乘5.6可以写作( ),还可以写作( );a乘h可以写作( ),还可以写作( )。
vt
5.6b
5.6·b
ah
a·h
一根绳子长48米,截成甲、乙两段,
其中,乙绳长度是甲绳的60%。
甲、乙两绳各长多少米?
总和关系
倍数关系
①多少分钟后,两人共折纸船40个?
(元元每分钟折纸船个数+路路每分钟折纸船个数)×时间=两人共折纸船个数
解:设 x 分钟后,两人共折纸船40个。
(5÷10+3÷10)x = 40
x = 50
答:50分钟后,两人共折纸船40个。
什么是方程的解?什么是解方程?怎样检验方程的解?
求方程的解的过程叫做解方程。
使方程左右两边相等的未知数的值叫做方程的解。
检验方程的解的方法:将未知数的值代入方程,看方程的左右两边是否相等。如果相等,所求的未知数的值就是方程的解,否则就不是。
体育室内足球的个数是篮球的75%,篮球比足球多6个。篮球和足球各有几个?
解:设篮球有X个,则足球有75%X个。
X-75%X=6
X=24
足球个数:75%X=75%×24=18个。
答:篮球有24个,足球有18个。
你会自己检验吗?
方程与等式的联系和区别
所有的方程都是等式,等式包括方程。
联系
所有的等式不一定是方程,等式范围更大;等式不一定含有未知数,方程必须含有未知数。
区别
新课讲解
两个粮库共存粮420 t,从甲粮库取出 的粮食到乙粮库,两个粮库的存粮就一样多了。原来甲粮库存粮多少吨?(先把线段图补充完整,再解答)[★★★★]
x
420-x
解:设原来甲粮库存粮 x t。
答:原来甲粮库存粮 270 t。
甲粮库存粮-甲粮库存粮× =乙粮库存粮+甲粮库存粮×
建筑工地上有一堆水泥,每天用a吨,用了5天,还剩下10吨。已经用去( )吨水泥,原来一共有( )吨水泥。
5a
5a+10
每天用a吨,5天就用了5个a吨,即a×5=5a(吨);用去的吨数加剩下的吨数就是原来一共有的吨数。
1.李奶奶家本月用电a千瓦时,比上个月多用10千瓦时,上个月用电
( )千瓦时。
2.如果每千瓦时电的价格是c元,李奶奶家本月的电费是( )元。
李奶奶家银行缴费卡上原有215元,扣除本月电费后,还剩( )元。
3.三个连续的自然数,最大的一个是n,那么最小的一个数是( )。
a-10
ac
215-ac
n-2
填一填。
课堂练习
(1)x=34是方程。 ( )
(2)a2一定比a3小。 ( )
√
判断。
×
(3)三个连续的自然数,最小的是a,这三个自然数的和是3a。 ( )
(4)如果n是自然数,那么2n+1一定是奇数。( )
(5)若b>a>0,则a的倒数比b的倒数大。 ( )
含有未知数的等式叫做方程。
当a=1或0时,a2=a3;当0<a<1时,a2>a3。
a+(a+1)+(a+2)=3a+3
2n一定是偶数,偶数加奇数一定等于奇数。
1
a
-和-比较大小,分子相同,分母越小,分数越大。
1
b
×
√
√
课堂小结
我的收获
等式的两边同时加上或减去同一个数(或式子),结果仍相等。
等式的两边同时乘或除以(0除外)
同一个数(或式子),结果仍相等。
课后作业
1、从教材课后习题中选取2、从课时练中选取
同学们再见
