高中数学人教A版(2019)选择性必修 第三册6.2.2排列数2 课件(共15张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)选择性必修 第三册6.2.2排列数2 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 219.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 19:24:58 | ||
图片预览




文档简介
(共15张PPT)
6.2.2排列数(二)
从n个不同元素中,任取m( )个元素(m个元素不可重复取)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
1、排列的定义:
2.排列数的定义:
从n个不同元素中,任取m( )个元素的所有排列的个数叫做从n个元素中取出m个元素的排列数
复习引入
3.全排列的定义:
n个不同元素全部取出的一个排列,叫做 n个不同元素的一个全排列.
4.有关公式:
(3)全排列数公式:
(2)排列数公式:
(1)阶乘:n!=1×2×3×…×(n-1)n
=n(n-1) ×…×(n-m+1)
=
(m、n∈N*,m≤n
例1、某年全国足球甲级A组联赛共有14个队参加,每队要与其余各队在主、客场分别比赛一次,共进行多少场比赛?
解:14个队中任意两队进行1次主场比赛与1次客场比赛,对应于从14个元素中任取2个元素的一个排列,因此,比赛的总场次是
例题讲评
例2:某信号兵用红,黄,蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可以任挂1面、2面或3面,并且不同的顺序表示不同的信号,一共可以表示多少种不同的信号?
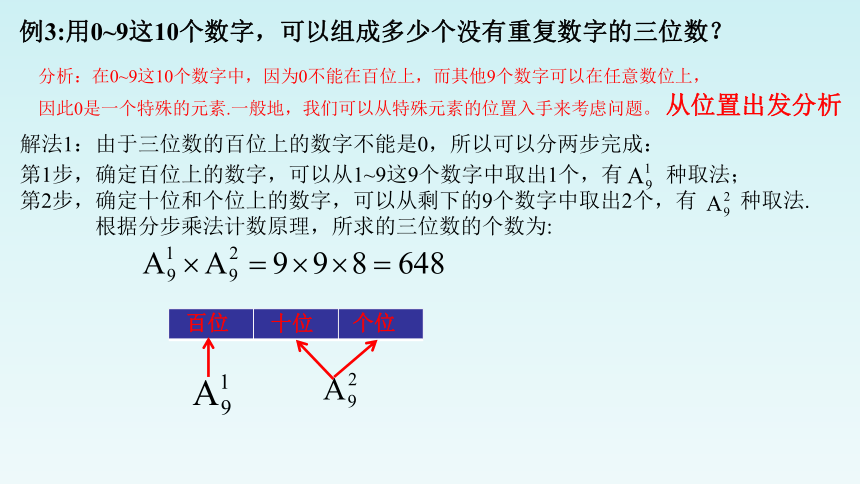
例3:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
分析:在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素.一般地,我们可以从特殊元素的位置入手来考虑问题。
解法1:由于三位数的百位上的数字不能是0,所以可以分两步完成:
第1步,确定百位上的数字,可以从1~9这9个数字中取出1个,有 种取法;
第2步,确定十位和个位上的数字,可以从剩下的9个数字中取出2个,有 种取法.
根据分步乘法计数原理,所求的三位数的个数为:
百位
十位
个位
从位置出发分析
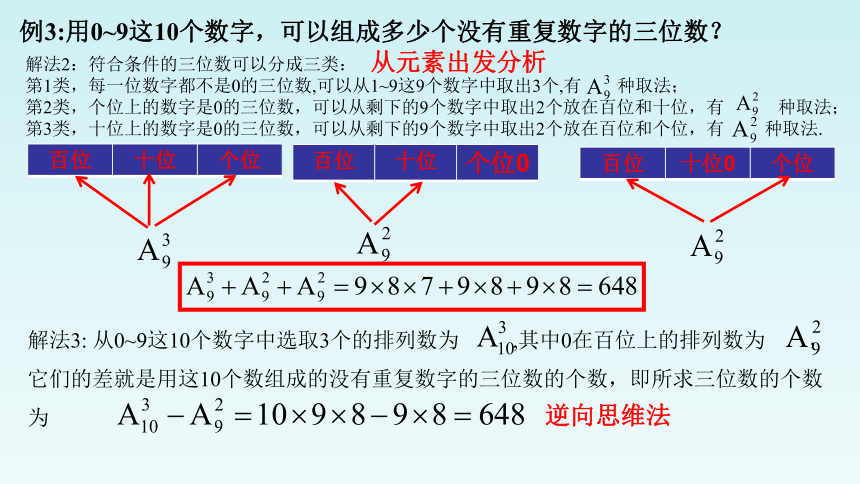
解法2:符合条件的三位数可以分成三类:
第1类,每一位数字都不是0的三位数,可以从1~9这9个数字中取出3个,有 种取法;
第2类,个位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和十位,有 种取法;
第3类,十位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和个位,有 种取法.
百位 十位 个位
百位 十位0 个位
百位 十位 个位0
例3:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法3: 从0~9这10个数字中选取3个的排列数为 ,其中0在百位上的排列数为 ,它们的差就是用这10个数组成的没有重复数字的三位数的个数,即所求三位数的个数为
逆向思维法
从元素出发分析
方法归纳:
1.求解排列问题的方法:
(1)判断排列问题;
(2)根据计数原理给出用排列数符号表示的运算式子;
(3)利用排列数公式求出结果。
2.带有限制条件的排列问题:“特殊”优先原则
直接法
间接法
位置分析法
元素分析法
以位置为主,优先考虑特殊位置
以元素为主,优先考虑特殊元素
先不考虑限制条件而计算出来所有排列数,再从中减去全部不符合条件的排列数,从而得出符合条件的排列数
百位
十位
个位
千位
万位
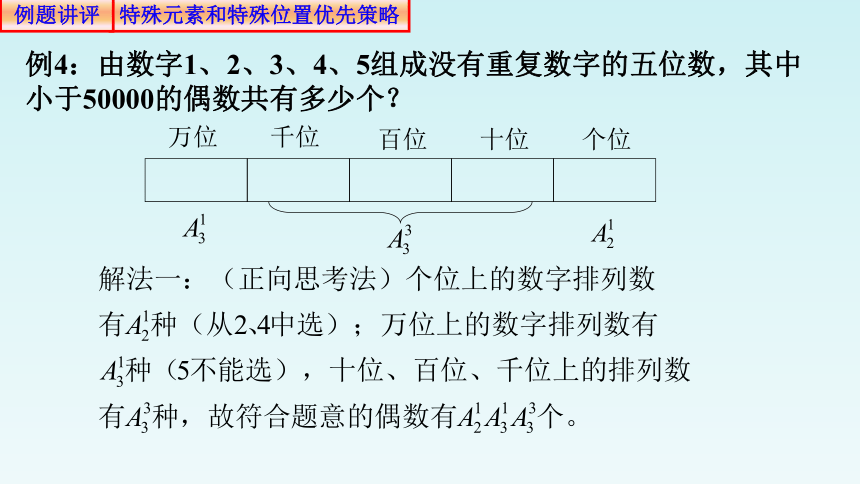
例4:由数字1、2、3、4、5组成没有重复数字的五位数,其中小于50000的偶数共有多少个?
特殊元素和特殊位置优先策略
例题讲评
百位
十位
个位
千位
万位
例4:由数字1、2、3、4、5组成没有重复数字的五位数,其中小于50000的偶数共有多少个?
特殊元素和特殊位置优先策略
例题讲评
用0-5这六个数字可以组成没有重复数字的
(1)四位偶数有多少个?奇数?
(5)十位数比个位数大的三位数?
(2)能被5整除的四位数有多少?
(3)能被3整除的四位数有多少?
(4)能被25整除的四位数有多少?
(6)能组成多少个比240135大的数?若把组成的全部六位数从小到大排列起来,那么240135是第几个数?
巩固练习
特殊元素和特殊位置优先策略
定序问题倍缩空位插入策略
例题讲评
例5. 7人排队,其中甲乙丙3人顺序一定(可以不相邻)共有多少不同的排法 ?
解:(倍缩法)对于某几个元素顺序一定的排列问题,可先把这几个元素与其他元素一起进行排列,然后用总排列数除以这几个元素之间的全排列数,则共有不同排法种数是:
(空位法)设想有7把椅子让除甲乙丙以外的四人就坐共有 种方法,其余的三个位置甲乙丙共有 1种坐法,则共有 种方法。
(插入法)先排甲乙丙三个人,共有1种排法,再把其余4四人依次插入共有4×5×6×7方法
例题讲评
例6. 8人围桌而坐,共有多少种坐法
环排问题线排策略
1.为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周.若课程“乐”不排在第一周,课程“御”不排在最后一周,则所有可能的排法种数为( )
A.216 B.480 C.504 D.624
巩固练习
2.某班星期三上午要上语文、数学、物理、历史、外语这五门课,若数学必须排在历史前面(可以不相邻),则五门课程不同的排法有( )
A.60种 B.30种 C.120种 D.24种
3.中国古代的五音一般指五声音阶,依次为:宫、商、角、微、羽,如果把这五个音阶全用上,排成一个5个音阶的音序,且要求宫、羽两音阶在角音阶的同侧,那么不同音序的排列种数为( )
A.120 B.90 C.80 D.60
巩固练习
4.从甲、乙、丙、丁、戊五名志愿者中选派三人分别从事翻译、导游、礼仪三项不同的工作,若乙和丙只能从事前两项工作,其余三人均能从事这三项工作,则不同的选派方案有( )
A.36种 B.12种 C.18种 D.24种
5. A,B,C,D,E,F六人围坐在一张圆桌周围开会,A是会议的中心发言人,必须坐最北面的椅子,B,C二人必须坐相邻的两把椅子,其余三人坐剩余的三把椅子,则不同的座次有( )
A.60种 B.48种 C.30种 D.24种
巩固练习
小结:
1.特殊元素,特殊位置优先安排策略
有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优先法);
位置分析法和元素分析法是解决排列组合问题最常用也是最基本的方法,若以元素分析为主,需先安排特殊元素,再处理其它元素.若以位置分析为主,需先满足特殊位置的要求,再处理其它位置。若有多个约束条件,往往是考虑一个约束条件的同时还要兼顾其它条件
2.定序问题可以用倍缩法,还可转化为占位插空.
6.2.2排列数(二)
从n个不同元素中,任取m( )个元素(m个元素不可重复取)按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
1、排列的定义:
2.排列数的定义:
从n个不同元素中,任取m( )个元素的所有排列的个数叫做从n个元素中取出m个元素的排列数
复习引入
3.全排列的定义:
n个不同元素全部取出的一个排列,叫做 n个不同元素的一个全排列.
4.有关公式:
(3)全排列数公式:
(2)排列数公式:
(1)阶乘:n!=1×2×3×…×(n-1)n
=n(n-1) ×…×(n-m+1)
=
(m、n∈N*,m≤n
例1、某年全国足球甲级A组联赛共有14个队参加,每队要与其余各队在主、客场分别比赛一次,共进行多少场比赛?
解:14个队中任意两队进行1次主场比赛与1次客场比赛,对应于从14个元素中任取2个元素的一个排列,因此,比赛的总场次是
例题讲评
例2:某信号兵用红,黄,蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可以任挂1面、2面或3面,并且不同的顺序表示不同的信号,一共可以表示多少种不同的信号?
例3:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
分析:在0~9这10个数字中,因为0不能在百位上,而其他9个数字可以在任意数位上,因此0是一个特殊的元素.一般地,我们可以从特殊元素的位置入手来考虑问题。
解法1:由于三位数的百位上的数字不能是0,所以可以分两步完成:
第1步,确定百位上的数字,可以从1~9这9个数字中取出1个,有 种取法;
第2步,确定十位和个位上的数字,可以从剩下的9个数字中取出2个,有 种取法.
根据分步乘法计数原理,所求的三位数的个数为:
百位
十位
个位
从位置出发分析
解法2:符合条件的三位数可以分成三类:
第1类,每一位数字都不是0的三位数,可以从1~9这9个数字中取出3个,有 种取法;
第2类,个位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和十位,有 种取法;
第3类,十位上的数字是0的三位数,可以从剩下的9个数字中取出2个放在百位和个位,有 种取法.
百位 十位 个位
百位 十位0 个位
百位 十位 个位0
例3:用0~9这10个数字,可以组成多少个没有重复数字的三位数?
解法3: 从0~9这10个数字中选取3个的排列数为 ,其中0在百位上的排列数为 ,它们的差就是用这10个数组成的没有重复数字的三位数的个数,即所求三位数的个数为
逆向思维法
从元素出发分析
方法归纳:
1.求解排列问题的方法:
(1)判断排列问题;
(2)根据计数原理给出用排列数符号表示的运算式子;
(3)利用排列数公式求出结果。
2.带有限制条件的排列问题:“特殊”优先原则
直接法
间接法
位置分析法
元素分析法
以位置为主,优先考虑特殊位置
以元素为主,优先考虑特殊元素
先不考虑限制条件而计算出来所有排列数,再从中减去全部不符合条件的排列数,从而得出符合条件的排列数
百位
十位
个位
千位
万位
例4:由数字1、2、3、4、5组成没有重复数字的五位数,其中小于50000的偶数共有多少个?
特殊元素和特殊位置优先策略
例题讲评
百位
十位
个位
千位
万位
例4:由数字1、2、3、4、5组成没有重复数字的五位数,其中小于50000的偶数共有多少个?
特殊元素和特殊位置优先策略
例题讲评
用0-5这六个数字可以组成没有重复数字的
(1)四位偶数有多少个?奇数?
(5)十位数比个位数大的三位数?
(2)能被5整除的四位数有多少?
(3)能被3整除的四位数有多少?
(4)能被25整除的四位数有多少?
(6)能组成多少个比240135大的数?若把组成的全部六位数从小到大排列起来,那么240135是第几个数?
巩固练习
特殊元素和特殊位置优先策略
定序问题倍缩空位插入策略
例题讲评
例5. 7人排队,其中甲乙丙3人顺序一定(可以不相邻)共有多少不同的排法 ?
解:(倍缩法)对于某几个元素顺序一定的排列问题,可先把这几个元素与其他元素一起进行排列,然后用总排列数除以这几个元素之间的全排列数,则共有不同排法种数是:
(空位法)设想有7把椅子让除甲乙丙以外的四人就坐共有 种方法,其余的三个位置甲乙丙共有 1种坐法,则共有 种方法。
(插入法)先排甲乙丙三个人,共有1种排法,再把其余4四人依次插入共有4×5×6×7方法
例题讲评
例6. 8人围桌而坐,共有多少种坐法
环排问题线排策略
1.为弘扬我国古代的“六艺文化”,某夏令营主办单位计划利用暑期开设“礼”“乐”“射”“御”“书”“数”六门体验课程,每周一门,连续开设六周.若课程“乐”不排在第一周,课程“御”不排在最后一周,则所有可能的排法种数为( )
A.216 B.480 C.504 D.624
巩固练习
2.某班星期三上午要上语文、数学、物理、历史、外语这五门课,若数学必须排在历史前面(可以不相邻),则五门课程不同的排法有( )
A.60种 B.30种 C.120种 D.24种
3.中国古代的五音一般指五声音阶,依次为:宫、商、角、微、羽,如果把这五个音阶全用上,排成一个5个音阶的音序,且要求宫、羽两音阶在角音阶的同侧,那么不同音序的排列种数为( )
A.120 B.90 C.80 D.60
巩固练习
4.从甲、乙、丙、丁、戊五名志愿者中选派三人分别从事翻译、导游、礼仪三项不同的工作,若乙和丙只能从事前两项工作,其余三人均能从事这三项工作,则不同的选派方案有( )
A.36种 B.12种 C.18种 D.24种
5. A,B,C,D,E,F六人围坐在一张圆桌周围开会,A是会议的中心发言人,必须坐最北面的椅子,B,C二人必须坐相邻的两把椅子,其余三人坐剩余的三把椅子,则不同的座次有( )
A.60种 B.48种 C.30种 D.24种
巩固练习
小结:
1.特殊元素,特殊位置优先安排策略
有特殊元素或特殊位置的排列问题,通常是先排特殊元素或特殊位置,称为优先处理特殊元素(位置)法(优先法);
位置分析法和元素分析法是解决排列组合问题最常用也是最基本的方法,若以元素分析为主,需先安排特殊元素,再处理其它元素.若以位置分析为主,需先满足特殊位置的要求,再处理其它位置。若有多个约束条件,往往是考虑一个约束条件的同时还要兼顾其它条件
2.定序问题可以用倍缩法,还可转化为占位插空.
