3.2.1 古典概型(下)和3.2.2随机的产生
文档属性
| 名称 | 3.2.1 古典概型(下)和3.2.2随机的产生 |

|
|
| 格式 | zip | ||
| 文件大小 | 186.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-09 19:37:19 | ||
图片预览








文档简介
课件20张PPT。3.2.1 古典概型
3.2.2 (整数值)随机数的产生
第二课时湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作1.我们将具有:
(1)试验中所有可能出现的基本事件只有 ;
(2)每个基本事件出现的可能性 . 这样两个特点的概率模型称为古典概率模型, 简称古典概型.知识回顾有限个相等古典概型的基本事件(试验中不能分的最简单的随机事件)有如下特点:
任何两个基本事件是互斥的;
任何事件(除不可能事件)都可以表示成基本事件的和.
3.2.1 古典概型2.古典概型计算任何事件的概率计算公式为:3.解决古典概型问题的关键:
求某个随机事件A包含的基本事件的个数和实验中基本事件的总数常用的方法是列举法
(画树型图和列表),注意做到不重不漏。 总数个数计算古典概型的概率的一般步骤:
看:阅读题目上,弄清题目中的背景材料,深刻理解题意,分析提炼出试验的基本事件;
定:判断试验是否为古典概型,设出所求事件并用字母表示出来;
算:分析并计算基本事件的总数,分析所求事件并计算所包含基本事件的个数
求:代入公式,求出该事件的概率.〖解〗每个密码相当于一个基本事件,共有10000个基本事件,即0000,0001,0002,…,9999.是一个古典概型.
其中事件A:“试一次密码就能取到钱”由1个基本事件构成. 例4 假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,2,…,9 十个数字中的任意一个.假设一个人完全忘记了自己的储蓄卡密码,问他到自动取款机上随机试一次密码就能取到钱的概率是多少?所以
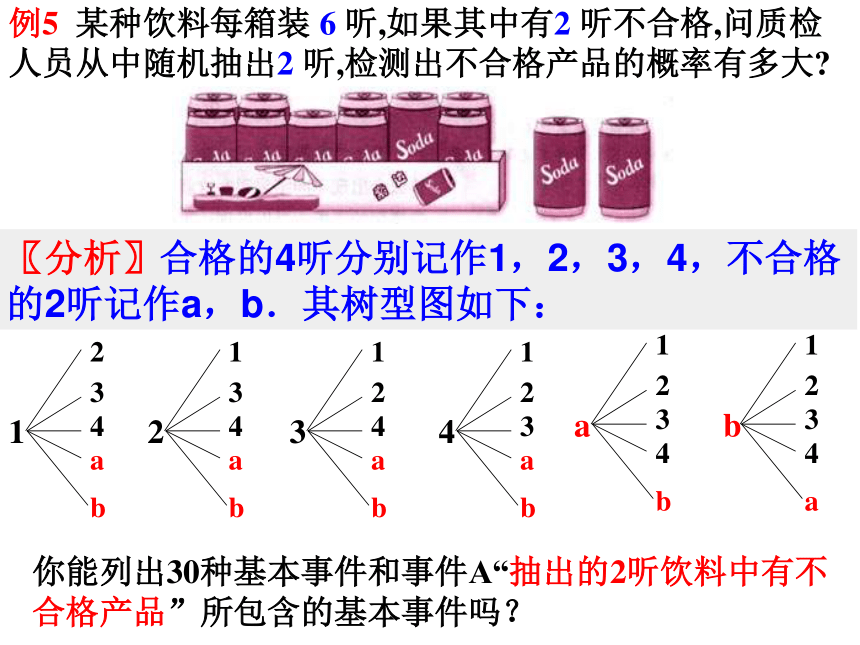
例5 某种饮料每箱装 6 听,如果其中有2 听不合格,问质检人员从中随机抽出2 听,检测出不合格产品的概率有多大?你能列出30种基本事件和事件A“抽出的2听饮料中有不合格产品”所包含的基本事件吗?〖分析〗合格的4听分别记作1,2,3,4,不合格的2听记作a,b.其树型图如下:
例5 某种饮料每箱装 6 听,如果其中有2 听不合格,问质检人员从中随机抽出2 听,检测出不合格产品的概率有多大?〖解〗合格的4听分别记作1,2,3,4,不合格的2听记作a,b.6听里随机抽出2听的所有基本事件共有30个,设检测出不合格产品的事件为A,事件A包括A1={仅第1次抽出的是不合格产品}、A2={仅第2次抽出的是不合格产品}、A3= ={两次抽出的都是不合格产品},且A1、A2、A3互斥,因此: 也可以用列表法来统计基本事件的总数及某事件包含的数据个数中学数理化www.shulihua.net例6、一个盒子里装有标号为1,2,3,4,5的5张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:
(1)标签的选取是不放回的;
(2)标签的选取是有放回的.中学数理化www.shulihua.net例7、 在一次口试中,要从5个题目中随机抽取3题进行回答,答对两题者为优秀,答对1题者为及格.某考生能回答其中2题.求:
(1)获得优秀的概率;
(2)获得及格或及格以上的概率.点拨:正难则反 中学数理化www.shulihua.net3.2.2 (整数值)随机数的产生中学数理化www.shulihua.net 前面我们做了大量重复的试验,同学们可能觉得耗时太多,那么,有无其他方法可以代替试验呢? -------随机模拟方法(蒙特卡罗方法)用计算器或计算机模拟试验的方法 产生随机数中学数理化www.shulihua.net产生随机数的方法有两种:一、由试验产生随机数 如:若产生1—25之间的随机整数,先将25个大小形状等均相同的小球分别标上1,2,…,24,25,放入一个袋中,把它们充分搅拌,然后从中摸出一个球,这个球上的数就是随机数。范围:所需要的随机数的个数不太多中学数理化www.shulihua.net二、由计算器或计算机产生随机数 由于计算器或计算机产生的随机数是根据确定的算法产生的,具有周期性(周期很长),具有类似随机数的性质,但并不是真正的随机数,而叫伪随机数。范围:所需要的随机数的个数较多中学数理化www.shulihua.net 下面将学习如何用计算器或计算机产生你指定的两个整数之间的取整数值的随机数1.用计算器产生随机数参阅教材P124及计算器相应说明书进行2.用计算机(Excel软件)产生随机数参阅教材P125步骤进行中学数理化www.shulihua.net例8、天气预报说,在今后的三天中,每一天下雨的概率均为40%,这三天中恰有两天下雨的概率是多少?分析:试验出现的可能结果是有限的,但每个结果的出现不是等可能的,所以不能用古典概型求概率。用计算器或计算机做模拟试验,可以模拟下于出现的概率是40%解:通过设计模拟试验的方法解决问题 利用计算器或计算机产生0—9之间去整数值的随机数。且用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,这样可以体现下雨的概率时40%。因为是3天,所以设三个随机数作为一组。如:产生20组随机数中学数理化www.shulihua.net907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 相当做了20次试验。在这组数中,若有两个数在1,2,3,4中,则表示恰有两天下雨,它们分别是:191 271 932 812 393(共5个数),因此,三天中恰有两天下雨的概率近似为5/20=25%想一想:你能体会随机模拟的好处吗?说明: (1)用计算器或计算机产生的随机数不是固定不变的
(2)用随机模拟的方法得到的是20次试验中恰有两天下雨的频率或概率的近似值,而不是概率。中学数理化www.shulihua.net小结:
古典概型的概率计算要注意:
(1)前提:每个基本事件的发生必须是等可能的
(2)关键:分清什么是基本事件?共有多少个?
符合条件的基本事件有多少个?
(3)基本事件的记数方法主要是:枚举法
-----通过“分类” 去枚举,找到 m, n
当从正面分类比较复杂时,可“从对立面”去枚举;
(4)注意:题中关键字“恰”、“至少”、“都”、“都不”
等的含义.“放回”与“不放回”的区别。练 习1. 一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球,从中摸出2个球,摸出2个黑球的概率是多少?2. 有5根细木棒,长度分别为1,3,5,7,9 (cm) ,从中任取3根,能搭成三角形的概率是多少?3. 从含有两件正品a1,a2和一件次品b的3件产品中每一次取1件,
(1)每次取出后不放回,连续取两次,求取出两件产品中恰有一件次品的概率;
(2)每次取出后放回,连续取两次,求取出两件产品中恰有一件次品的概率。解(1)基本事件有(a1,a2) , (a1,b) , (a2,a1) , (a2,b) , (b,a1) , (b,a2)共6个. 恰有一件次品的基本事件有(a1,b) , (a2,b) , (b,a1) , (b,a2)有4个. 则恰有一件次品的概率为P=4/6=2/3;(2)基本事件有:恰有一件次品的概率为P=4/9.准确把握不同条件下的基本事件的总数
3.2.2 (整数值)随机数的产生
第二课时湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作1.我们将具有:
(1)试验中所有可能出现的基本事件只有 ;
(2)每个基本事件出现的可能性 . 这样两个特点的概率模型称为古典概率模型, 简称古典概型.知识回顾有限个相等古典概型的基本事件(试验中不能分的最简单的随机事件)有如下特点:
任何两个基本事件是互斥的;
任何事件(除不可能事件)都可以表示成基本事件的和.
3.2.1 古典概型2.古典概型计算任何事件的概率计算公式为:3.解决古典概型问题的关键:
求某个随机事件A包含的基本事件的个数和实验中基本事件的总数常用的方法是列举法
(画树型图和列表),注意做到不重不漏。 总数个数计算古典概型的概率的一般步骤:
看:阅读题目上,弄清题目中的背景材料,深刻理解题意,分析提炼出试验的基本事件;
定:判断试验是否为古典概型,设出所求事件并用字母表示出来;
算:分析并计算基本事件的总数,分析所求事件并计算所包含基本事件的个数
求:代入公式,求出该事件的概率.〖解〗每个密码相当于一个基本事件,共有10000个基本事件,即0000,0001,0002,…,9999.是一个古典概型.
其中事件A:“试一次密码就能取到钱”由1个基本事件构成. 例4 假设储蓄卡的密码由4个数字组成,每个数字可以是0,1,2,…,9 十个数字中的任意一个.假设一个人完全忘记了自己的储蓄卡密码,问他到自动取款机上随机试一次密码就能取到钱的概率是多少?所以
例5 某种饮料每箱装 6 听,如果其中有2 听不合格,问质检人员从中随机抽出2 听,检测出不合格产品的概率有多大?你能列出30种基本事件和事件A“抽出的2听饮料中有不合格产品”所包含的基本事件吗?〖分析〗合格的4听分别记作1,2,3,4,不合格的2听记作a,b.其树型图如下:
例5 某种饮料每箱装 6 听,如果其中有2 听不合格,问质检人员从中随机抽出2 听,检测出不合格产品的概率有多大?〖解〗合格的4听分别记作1,2,3,4,不合格的2听记作a,b.6听里随机抽出2听的所有基本事件共有30个,设检测出不合格产品的事件为A,事件A包括A1={仅第1次抽出的是不合格产品}、A2={仅第2次抽出的是不合格产品}、A3= ={两次抽出的都是不合格产品},且A1、A2、A3互斥,因此: 也可以用列表法来统计基本事件的总数及某事件包含的数据个数中学数理化www.shulihua.net例6、一个盒子里装有标号为1,2,3,4,5的5张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:
(1)标签的选取是不放回的;
(2)标签的选取是有放回的.中学数理化www.shulihua.net例7、 在一次口试中,要从5个题目中随机抽取3题进行回答,答对两题者为优秀,答对1题者为及格.某考生能回答其中2题.求:
(1)获得优秀的概率;
(2)获得及格或及格以上的概率.点拨:正难则反 中学数理化www.shulihua.net3.2.2 (整数值)随机数的产生中学数理化www.shulihua.net 前面我们做了大量重复的试验,同学们可能觉得耗时太多,那么,有无其他方法可以代替试验呢? -------随机模拟方法(蒙特卡罗方法)用计算器或计算机模拟试验的方法 产生随机数中学数理化www.shulihua.net产生随机数的方法有两种:一、由试验产生随机数 如:若产生1—25之间的随机整数,先将25个大小形状等均相同的小球分别标上1,2,…,24,25,放入一个袋中,把它们充分搅拌,然后从中摸出一个球,这个球上的数就是随机数。范围:所需要的随机数的个数不太多中学数理化www.shulihua.net二、由计算器或计算机产生随机数 由于计算器或计算机产生的随机数是根据确定的算法产生的,具有周期性(周期很长),具有类似随机数的性质,但并不是真正的随机数,而叫伪随机数。范围:所需要的随机数的个数较多中学数理化www.shulihua.net 下面将学习如何用计算器或计算机产生你指定的两个整数之间的取整数值的随机数1.用计算器产生随机数参阅教材P124及计算器相应说明书进行2.用计算机(Excel软件)产生随机数参阅教材P125步骤进行中学数理化www.shulihua.net例8、天气预报说,在今后的三天中,每一天下雨的概率均为40%,这三天中恰有两天下雨的概率是多少?分析:试验出现的可能结果是有限的,但每个结果的出现不是等可能的,所以不能用古典概型求概率。用计算器或计算机做模拟试验,可以模拟下于出现的概率是40%解:通过设计模拟试验的方法解决问题 利用计算器或计算机产生0—9之间去整数值的随机数。且用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,这样可以体现下雨的概率时40%。因为是3天,所以设三个随机数作为一组。如:产生20组随机数中学数理化www.shulihua.net907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 相当做了20次试验。在这组数中,若有两个数在1,2,3,4中,则表示恰有两天下雨,它们分别是:191 271 932 812 393(共5个数),因此,三天中恰有两天下雨的概率近似为5/20=25%想一想:你能体会随机模拟的好处吗?说明: (1)用计算器或计算机产生的随机数不是固定不变的
(2)用随机模拟的方法得到的是20次试验中恰有两天下雨的频率或概率的近似值,而不是概率。中学数理化www.shulihua.net小结:
古典概型的概率计算要注意:
(1)前提:每个基本事件的发生必须是等可能的
(2)关键:分清什么是基本事件?共有多少个?
符合条件的基本事件有多少个?
(3)基本事件的记数方法主要是:枚举法
-----通过“分类” 去枚举,找到 m, n
当从正面分类比较复杂时,可“从对立面”去枚举;
(4)注意:题中关键字“恰”、“至少”、“都”、“都不”
等的含义.“放回”与“不放回”的区别。练 习1. 一个口袋内装有大小相等的1个白球和已编有不同号码的3个黑球,从中摸出2个球,摸出2个黑球的概率是多少?2. 有5根细木棒,长度分别为1,3,5,7,9 (cm) ,从中任取3根,能搭成三角形的概率是多少?3. 从含有两件正品a1,a2和一件次品b的3件产品中每一次取1件,
(1)每次取出后不放回,连续取两次,求取出两件产品中恰有一件次品的概率;
(2)每次取出后放回,连续取两次,求取出两件产品中恰有一件次品的概率。解(1)基本事件有(a1,a2) , (a1,b) , (a2,a1) , (a2,b) , (b,a1) , (b,a2)共6个. 恰有一件次品的基本事件有(a1,b) , (a2,b) , (b,a1) , (b,a2)有4个. 则恰有一件次品的概率为P=4/6=2/3;(2)基本事件有:恰有一件次品的概率为P=4/9.准确把握不同条件下的基本事件的总数
