人教版数学八年级下册19.2.3一次函数与二元一次方程组 课件(共17张PPT)
文档属性
| 名称 | 人教版数学八年级下册19.2.3一次函数与二元一次方程组 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 763.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 06:45:38 | ||
图片预览





文档简介
(共17张PPT)
一次函数与二元一次方程组
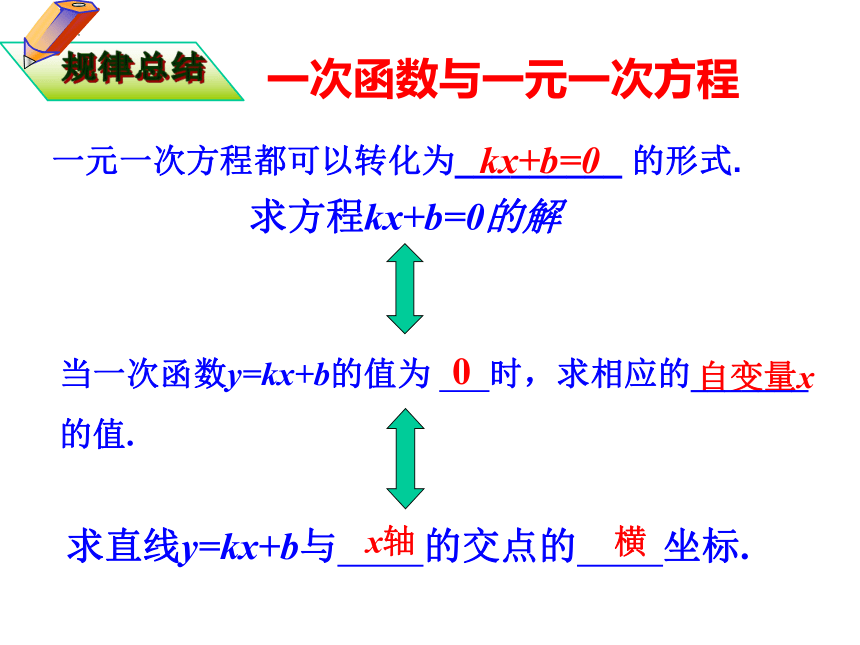
一元一次方程都可以转化为_________ 的形式.
kx+b=0
0
自变量x
求直线y=kx+b与 的交点的 坐标.
x轴
横
当一次函数y=kx+b的值为 时,求相应的_______
的值.
求方程kx+b=0的解
规律总结
一次函数与一元一次方程
规律总结
从数的角度看
求ax+b>0(或<0)(a≠0)的解
从形的角度看
求ax+b>0(或<0)(a≠0)的解
x为何值时y=ax+b的值大于0(或小于0)
确定直线y=ax+b在x轴上方(或下方) 的图象所对应的x的取值范围
一次函数与一元一次不等式
八年级 数学
第十四章 函数
一次函数与二元一次方程组
一次函数
这是怎么回事?
二元一次方程
y-x=1
y=x+1
y=x+1这是什么?
(1)对于方程2x+5y =8如何用x表示y
(3)一次函数的图象是一条直线,对于直线上每个点的坐标(x ,y),那么 x 、y 是不是对应方程的解呢
y = .
(2)是不是任意的二元一次方程都能进行这样的转化呢?
(1)3x - y =0
(2) x + y = 6
活动一: 探究一次函数与二元一次方程的关系
即: 二元一次方程 (数)
相应的一次函数的图象(形)
对应
结论:
以二元一次方程的解为坐标的点都在相应的函数图象上.反过来,
一次函数图象上的点的坐标都适合相应的二元一次方程.
(1)在同一直角坐标系中画
y = x +
与 y = 2 x - 1的图象
这个交点(1,1)是
方程组
的解吗
活动二: 探究一次函数图像上的点与二元一次方程组的解
的关系
是否任意两个一次函数的交点坐标都是它们所对应的二元一次方程组的解?
是
是
y = x +
与 y = 2 x - 1的值相等
这个函数值是多少
(2)当自变量x取何值时,函数
与解方程组:
是同一个问题吗
X=1
y=1
是
归纳总结:
从数的角度看:
从形的角度看:
求二元一次方程组的解
x为何值时,两个函数的值相等以及这个函数值是何值
求二元一次方程组的解
确定两条直线交点的坐标
一次函数与二元一次方程组
1、根据下列图象,你能说出它表示哪个方程组的解?这个解是什么?
1
1
x
y
o
y=2x-1
y=-3x+4
实践应用
活动三: 利用函数图像解方程
方程组
2x–y= 1
3x+y=4
x=1
y=1
2x+y=4
2x-3y=12
2:用图象法解方程组:
①
②
解:
由①得:
由②得:
作出图象:
观察图象得:交点(3,-2)
∴方程组的解为
x=3
y=-2
x
o
y
y=-2x+4
y=2/3x - 4
二元一次方程组的解与以这两个方程所对应的一次函数图象的交点坐标相对应。
由此可得:
二元一次方程组的图象解法.
步骤:写函数,作图象、找交点,下结论
归纳总结
你能用不同的方法解决吗
应 用
例1 一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按上网时间计费。上网时间为多少分,两种方式的计费相等?
两个函数的图像交于点(400,40)。
这表示当x=400时,两个函数的值都等于
40,因此,上网时间为400分,两种方式
的计费相等(都是40元)。
y=0.1x
y=0.05x+20
解法2:解方程组
y=0.1x
y=0.05x+20
解得
x=400
y=40
本题解法与解方程组 具有同样的效果
2.为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(分钟与通话费y元的关系如图所示:
应用与拓展
问题:1、通话多少分钟
两种卡花费一样?
120
40
x
y
o
60
20
40
20
10
30
100
80
50
y=0.5x
y=30+0.2x
便民卡
如意卡
(分)
(元)
2、通话多少分钟
便民卡优惠?
3、通话多少分钟
如意卡优惠?
市内通话问题
全球通:月租费50元,0.4元/分
神州行:0.6元/分
如何选择计费方式更省钱
随堂练习
你能用不同方法吗?.
再见!
一次函数与二元一次方程组
一元一次方程都可以转化为_________ 的形式.
kx+b=0
0
自变量x
求直线y=kx+b与 的交点的 坐标.
x轴
横
当一次函数y=kx+b的值为 时,求相应的_______
的值.
求方程kx+b=0的解
规律总结
一次函数与一元一次方程
规律总结
从数的角度看
求ax+b>0(或<0)(a≠0)的解
从形的角度看
求ax+b>0(或<0)(a≠0)的解
x为何值时y=ax+b的值大于0(或小于0)
确定直线y=ax+b在x轴上方(或下方) 的图象所对应的x的取值范围
一次函数与一元一次不等式
八年级 数学
第十四章 函数
一次函数与二元一次方程组
一次函数
这是怎么回事?
二元一次方程
y-x=1
y=x+1
y=x+1这是什么?
(1)对于方程2x+5y =8如何用x表示y
(3)一次函数的图象是一条直线,对于直线上每个点的坐标(x ,y),那么 x 、y 是不是对应方程的解呢
y = .
(2)是不是任意的二元一次方程都能进行这样的转化呢?
(1)3x - y =0
(2) x + y = 6
活动一: 探究一次函数与二元一次方程的关系
即: 二元一次方程 (数)
相应的一次函数的图象(形)
对应
结论:
以二元一次方程的解为坐标的点都在相应的函数图象上.反过来,
一次函数图象上的点的坐标都适合相应的二元一次方程.
(1)在同一直角坐标系中画
y = x +
与 y = 2 x - 1的图象
这个交点(1,1)是
方程组
的解吗
活动二: 探究一次函数图像上的点与二元一次方程组的解
的关系
是否任意两个一次函数的交点坐标都是它们所对应的二元一次方程组的解?
是
是
y = x +
与 y = 2 x - 1的值相等
这个函数值是多少
(2)当自变量x取何值时,函数
与解方程组:
是同一个问题吗
X=1
y=1
是
归纳总结:
从数的角度看:
从形的角度看:
求二元一次方程组的解
x为何值时,两个函数的值相等以及这个函数值是何值
求二元一次方程组的解
确定两条直线交点的坐标
一次函数与二元一次方程组
1、根据下列图象,你能说出它表示哪个方程组的解?这个解是什么?
1
1
x
y
o
y=2x-1
y=-3x+4
实践应用
活动三: 利用函数图像解方程
方程组
2x–y= 1
3x+y=4
x=1
y=1
2x+y=4
2x-3y=12
2:用图象法解方程组:
①
②
解:
由①得:
由②得:
作出图象:
观察图象得:交点(3,-2)
∴方程组的解为
x=3
y=-2
x
o
y
y=-2x+4
y=2/3x - 4
二元一次方程组的解与以这两个方程所对应的一次函数图象的交点坐标相对应。
由此可得:
二元一次方程组的图象解法.
步骤:写函数,作图象、找交点,下结论
归纳总结
你能用不同的方法解决吗
应 用
例1 一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网时间计费;方式B除收月基费20元外再以每分0.05元的价格按上网时间计费。上网时间为多少分,两种方式的计费相等?
两个函数的图像交于点(400,40)。
这表示当x=400时,两个函数的值都等于
40,因此,上网时间为400分,两种方式
的计费相等(都是40元)。
y=0.1x
y=0.05x+20
解法2:解方程组
y=0.1x
y=0.05x+20
解得
x=400
y=40
本题解法与解方程组 具有同样的效果
2.为了发展电信事业,方便用户,电信公司对移动电话采用不同的收费方式,其中使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(分钟与通话费y元的关系如图所示:
应用与拓展
问题:1、通话多少分钟
两种卡花费一样?
120
40
x
y
o
60
20
40
20
10
30
100
80
50
y=0.5x
y=30+0.2x
便民卡
如意卡
(分)
(元)
2、通话多少分钟
便民卡优惠?
3、通话多少分钟
如意卡优惠?
市内通话问题
全球通:月租费50元,0.4元/分
神州行:0.6元/分
如何选择计费方式更省钱
随堂练习
你能用不同方法吗?.
再见!
