人教版七年级下数学第六章 实数复习课件(共18张PPT)
文档属性
| 名称 | 人教版七年级下数学第六章 实数复习课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 337.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 07:12:26 | ||
图片预览





文档简介
(共18张PPT)
第六章 实数复习课
1、归纳和整理本章知识点,形成系统知识;
2、强化对平方根、算术平方根、立方根、实数等相关概
念的理解;
3、能进行简单的实数相关运算。
复习目标
课前准备
1.算术平方根
如果一个正数x的平方等于即,那么x叫做的算术平方根,记作;0的算术平方根是0; ≥0(≥0)。
2.平方根
(1)定义:如果一个数x的平方等于,则x叫做的平方根,记作,0的平方根是0。
(2)性质:
①正数有两个平方根,它们互为相反数;
②0的平方根是0;
③负数没有平方根。
3.立方根
(1)定义:如果一个数x的立方等于a,则x叫做a的立方根,记作______,0的立方根是0。
(2)性质:
①正数的立方根是正数;
②负数的立方根是负数;
③0的立方根是0。
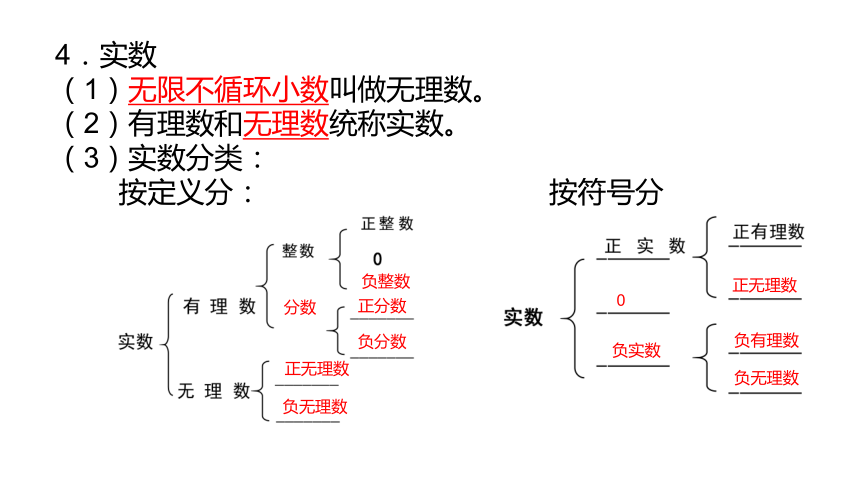
4.实数
(1)无限不循环小数叫做无理数。
(2)有理数和无理数统称实数。
(3)实数分类:
按定义分: 按符号分
分数
负整数
负分数
正分数
正无理数
负无理数
负无理数
负有理数
正无理数
负实数
0
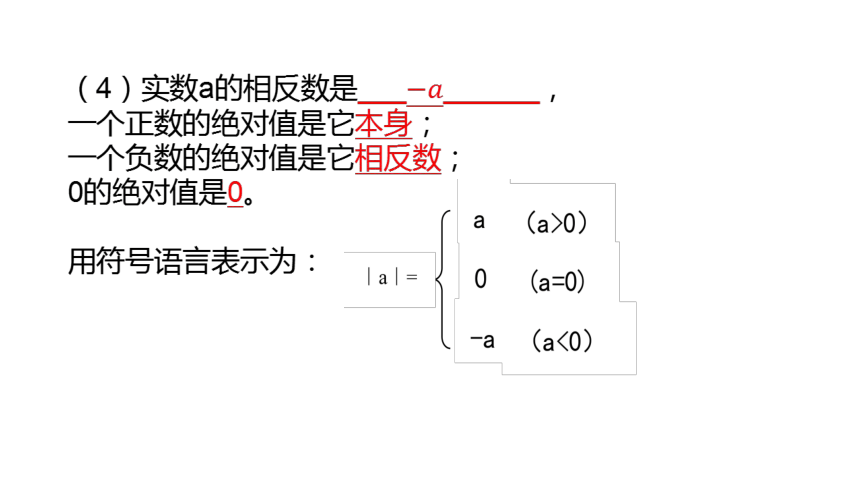
(4)实数a的相反数是_________,
一个正数的绝对值是它本身;
一个负数的绝对值是它相反数;
0的绝对值是0。
用符号语言表示为:
(5)实数性质:实数与数轴上的点是一一对应的,有理数
的运算法则、运算律等在实数范围内同样适用。
(6)三个非负性: ≥0, ≥0, ≥0。(a≥0)
二.无理数的概念
(1)下列各数是无理数的是( )
A.0 B.-1 C. D.
(2)下列各数中,3.141 59, ,0.131 131 113…,-π, , ,
无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
C
C
(1)和数轴上的点一一对应的是( )
A.整数 B.有理数 C.无理数 D.实数
(2)数轴上的两个点A,B所表示的数分别是a,b,在a+b,a-b,
ab,|a|-|b|中,是正数的有____个.
三.实数与数轴
D
1
四.实数大小的比较
(1)在实数 、-2,、0、 中,最小实数是( )
A.-2 B.0 C. D.
(2)设n为正整数,且n< <n+1,则的值为( )
A.4 B.5 C.6 D. 7
A
B
五.实数的运算
(1)化简: =_____________.
(2)计算:
六.实数的非负性
(1)若数m,n满足 ,则 =__________.
(2)已知实数x,y满足 ,则代数式 的值为___________.
七.延伸与拓展
(1)求下列式子中的x:
① x2=9 ②4x2=36 ③ 4(x-1)2=36 ④4(2x-1)2=36.
(2)已知2a-1的平方根是±3,3a+b-1的平方根是±4,求a+2b的平方根.
1.本章有哪些知识点?
2.本节课渗透了哪些数学思想?
3.知识结构:
4.特别注意 、 、 、 所表示的意义。
课堂小结
当堂检测
1.选择题
(1)25的平方根是( )
A.5 B.-5 C.±5 D.
(2)下列说法不正确的是( )
A.8的立方根是2 B.-8的立方根是-2
C.0的立方根是0 D.125的立方根是±5
(3)在实数:3.141 59, ,1.010 010 001, ,π, 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
C
D
A
2.填空题
(1) 的算术平方根是________.
(2) 的相反数是_________,绝对值是__________.
(3)计算: =___________.
3.解答题
已知2a-1的平方根是±3, 的算术平方根是b,求 .
第六章 实数复习课
1、归纳和整理本章知识点,形成系统知识;
2、强化对平方根、算术平方根、立方根、实数等相关概
念的理解;
3、能进行简单的实数相关运算。
复习目标
课前准备
1.算术平方根
如果一个正数x的平方等于即,那么x叫做的算术平方根,记作;0的算术平方根是0; ≥0(≥0)。
2.平方根
(1)定义:如果一个数x的平方等于,则x叫做的平方根,记作,0的平方根是0。
(2)性质:
①正数有两个平方根,它们互为相反数;
②0的平方根是0;
③负数没有平方根。
3.立方根
(1)定义:如果一个数x的立方等于a,则x叫做a的立方根,记作______,0的立方根是0。
(2)性质:
①正数的立方根是正数;
②负数的立方根是负数;
③0的立方根是0。
4.实数
(1)无限不循环小数叫做无理数。
(2)有理数和无理数统称实数。
(3)实数分类:
按定义分: 按符号分
分数
负整数
负分数
正分数
正无理数
负无理数
负无理数
负有理数
正无理数
负实数
0
(4)实数a的相反数是_________,
一个正数的绝对值是它本身;
一个负数的绝对值是它相反数;
0的绝对值是0。
用符号语言表示为:
(5)实数性质:实数与数轴上的点是一一对应的,有理数
的运算法则、运算律等在实数范围内同样适用。
(6)三个非负性: ≥0, ≥0, ≥0。(a≥0)
二.无理数的概念
(1)下列各数是无理数的是( )
A.0 B.-1 C. D.
(2)下列各数中,3.141 59, ,0.131 131 113…,-π, , ,
无理数的个数有( )
A.1个 B.2个 C.3个 D.4个
C
C
(1)和数轴上的点一一对应的是( )
A.整数 B.有理数 C.无理数 D.实数
(2)数轴上的两个点A,B所表示的数分别是a,b,在a+b,a-b,
ab,|a|-|b|中,是正数的有____个.
三.实数与数轴
D
1
四.实数大小的比较
(1)在实数 、-2,、0、 中,最小实数是( )
A.-2 B.0 C. D.
(2)设n为正整数,且n< <n+1,则的值为( )
A.4 B.5 C.6 D. 7
A
B
五.实数的运算
(1)化简: =_____________.
(2)计算:
六.实数的非负性
(1)若数m,n满足 ,则 =__________.
(2)已知实数x,y满足 ,则代数式 的值为___________.
七.延伸与拓展
(1)求下列式子中的x:
① x2=9 ②4x2=36 ③ 4(x-1)2=36 ④4(2x-1)2=36.
(2)已知2a-1的平方根是±3,3a+b-1的平方根是±4,求a+2b的平方根.
1.本章有哪些知识点?
2.本节课渗透了哪些数学思想?
3.知识结构:
4.特别注意 、 、 、 所表示的意义。
课堂小结
当堂检测
1.选择题
(1)25的平方根是( )
A.5 B.-5 C.±5 D.
(2)下列说法不正确的是( )
A.8的立方根是2 B.-8的立方根是-2
C.0的立方根是0 D.125的立方根是±5
(3)在实数:3.141 59, ,1.010 010 001, ,π, 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
C
D
A
2.填空题
(1) 的算术平方根是________.
(2) 的相反数是_________,绝对值是__________.
(3)计算: =___________.
3.解答题
已知2a-1的平方根是±3, 的算术平方根是b,求 .
