2020-2021年全国各省高考物理试题分类汇编:万有引力与航天(word版含答案)
文档属性
| 名称 | 2020-2021年全国各省高考物理试题分类汇编:万有引力与航天(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 606.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-05-18 00:00:00 | ||
图片预览




文档简介
2020-2021年全国各省高考物理试题分类汇编:万有引力与航天
一、单选题(本大题共8小题)
1.(2021·浙江·高考真题)“天问一号”从地球发射后,在如图甲所示的P点沿地火转移轨道到Q点,再依次进入如图乙所示的调相轨道和停泊轨道,则天问一号( )
A.发射速度介于7.9km/s与11.2km/s之间
B.从P点转移到Q点的时间小于6个月
C.在环绕火星的停泊轨道运行的周期比在调相轨道上小
D.在地火转移轨道运动时的速度均大于地球绕太阳的速度
2.(2021·江苏·高考真题)我国航天人发扬“两弹一星”精神砥砺前行,从“东方红一号”到“北斗”不断创造奇迹。“北斗”第49颗卫星的发射迈出组网的关键一步。该卫星绕地球做圆周运动,运动周期与地球自转周期相同,轨道平面与地球赤道平面成一定夹角。该卫星( )
A.运动速度大于第一宇宙速度
B.运动速度小于第一宇宙速度
C.轨道半径大于“静止”在赤道上空的同步卫星
D.轨道半径小于“静止”在赤道上空的同步卫星
3.(2021·湖北·高考真题)2021年5月,天问一号探测器软着陆火星取得成功,迈出了我国星际探测征程的重要一步。火星与地球公转轨道近似为圆,两轨道平面近似重合,且火星与地球公转方向相同。火星与地球每隔约26个月相距最近,地球公转周期为12个月。由以上条件可以近似得出( )
A.地球与火星的动能之比
B.地球与火星的自转周期之比
C.地球表面与火星表面重力加速度大小之比
D.地球与火星绕太阳运动的向心加速度大小之比
4.(2021·天津·高考真题)2021年5月15日,天问一号探测器着陆火星取得成功,迈出了我国星际探测征程的重要一步,在火星上首次留下国人的印迹。天问一号探测器成功发射后,顺利被火星捕获,成为我国第一颗人造火星卫星。经过轨道调整,探测器先沿椭圆轨道Ⅰ运行,之后进入称为火星停泊轨道的椭圆轨道Ⅱ运行,如图所示,两轨道相切于近火点P,则天问一号探测器( )
A.在轨道Ⅱ上处于受力平衡状态 B.在轨道Ⅰ运行周期比在Ⅱ时短
C.从轨道Ⅰ进入Ⅱ在P处要加速 D.沿轨道Ⅰ向P飞近时速度增大
5.(2021·山东·高考真题)从“玉兔”登月到“祝融”探火,我国星际探测事业实现了由地月系到行星际的跨越。已知火星质量约为月球的9倍,半径约为月球的2倍,“祝融”火星车的质量约为“玉兔”月球车的2倍。在着陆前,“祝融”和“玉兔”都会经历一个由着陆平台支撑的悬停过程。悬停时,“祝融”与“玉兔”所受陆平台的作用力大小之比为( )
A.9∶1 B.9∶2 C.36∶1 D.72∶1
6.(2021·全国·高考真题)科学家对银河系中心附近的恒星S2进行了多年的持续观测,给出1994年到2002年间S2的位置如图所示。科学家认为S2的运动轨迹是半长轴约为(太阳到地球的距离为)的椭圆,银河系中心可能存在超大质量黑洞。这项研究工作获得了2020年诺贝尔物理学奖。若认为S2所受的作用力主要为该大质量黑洞的引力,设太阳的质量为M,可以推测出该黑洞质量约为( )
A. B. C. D.
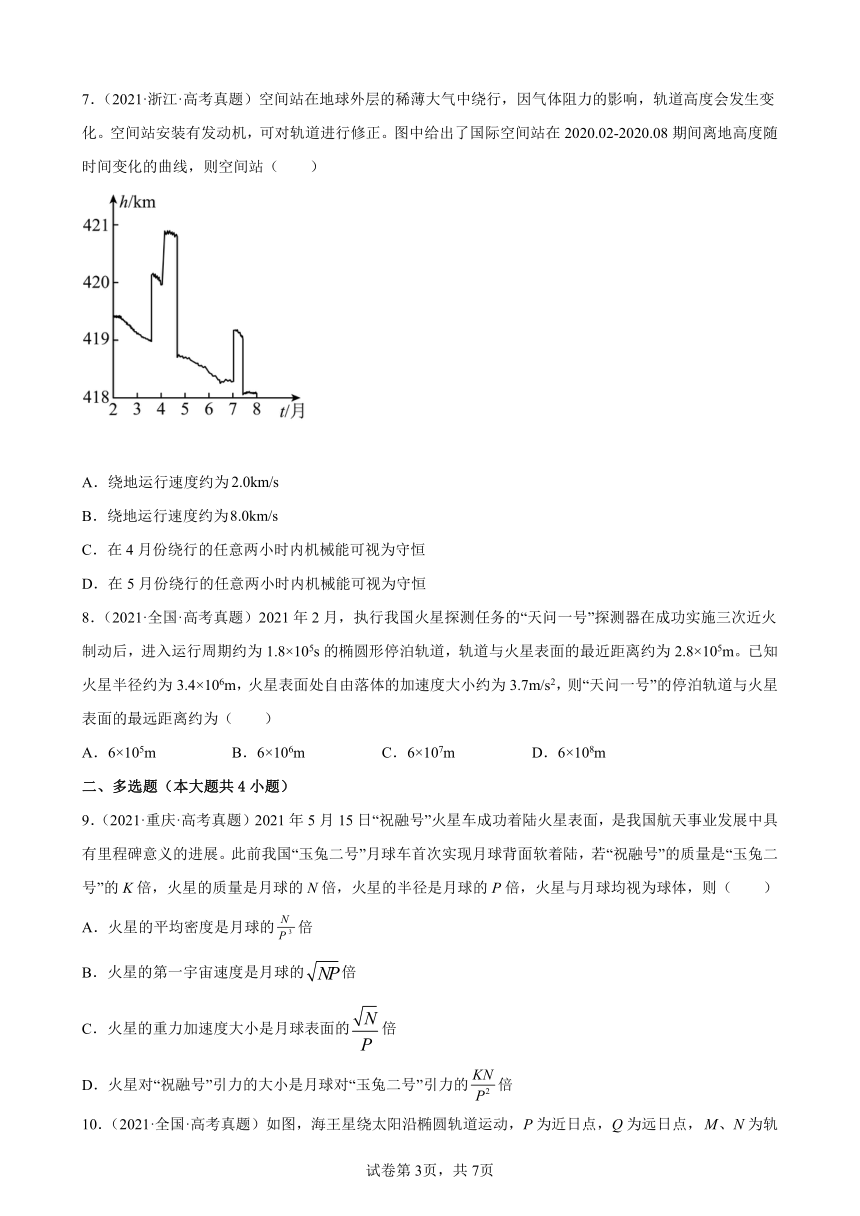
7.(2021·浙江·高考真题)空间站在地球外层的稀薄大气中绕行,因气体阻力的影响,轨道高度会发生变化。空间站安装有发动机,可对轨道进行修正。图中给出了国际空间站在2020.02-2020.08期间离地高度随时间变化的曲线,则空间站( )
A.绕地运行速度约为
B.绕地运行速度约为
C.在4月份绕行的任意两小时内机械能可视为守恒
D.在5月份绕行的任意两小时内机械能可视为守恒
8.(2021·全国·高考真题)2021年2月,执行我国火星探测任务的“天问一号”探测器在成功实施三次近火制动后,进入运行周期约为1.8×105s的椭圆形停泊轨道,轨道与火星表面的最近距离约为2.8×105m。已知火星半径约为3.4×106m,火星表面处自由落体的加速度大小约为3.7m/s2,则“天问一号”的停泊轨道与火星表面的最远距离约为( )
A.6×105m B.6×106m C.6×107m D.6×108m
二、多选题(本大题共4小题)
9.(2021·重庆·高考真题)2021年5月15日“祝融号”火星车成功着陆火星表面,是我国航天事业发展中具有里程碑意义的进展。此前我国“玉兔二号”月球车首次实现月球背面软着陆,若“祝融号”的质量是“玉兔二号”的K倍,火星的质量是月球的N倍,火星的半径是月球的P倍,火星与月球均视为球体,则( )
A.火星的平均密度是月球的倍
B.火星的第一宇宙速度是月球的倍
C.火星的重力加速度大小是月球表面的倍
D.火星对“祝融号”引力的大小是月球对“玉兔二号”引力的倍
10.(2021·全国·高考真题)如图,海王星绕太阳沿椭圆轨道运动,P为近日点,Q为远日点,为轨道短轴的两个端点,运行的周期为。若只考虑海王星和太阳之间的相互作用,则海王星在从P经到N的运动过程中( )
A.从P到M所用的时间等于
B.从Q到N阶段,机械能逐渐变大
C.从P到Q阶段,速率逐渐变小
D.从M到N阶段,万有引力对它先做负功后做正功
11.(2021·福建·高考真题)两位科学家因为在银河系中心发现了一个超大质量的致密天体而获得了2020年诺贝尔物理学奖。他们对一颗靠近银河系中心的恒星的位置变化进行了持续观测,记录到的的椭圆轨道如图所示。图中O为椭圆的一个焦点,椭圆偏心率(离心率)约为0.87。P、Q分别为轨道的远银心点和近银心点,Q与O的距离约为(太阳到地球的距离为),的运行周期约为16年。假设的运动轨迹主要受银河系中心致密天体的万有引力影响,根据上述数据及日常的天文知识,可以推出( )
A.与银河系中心致密天体的质量之比
B.银河系中心致密天体与太阳的质量之比
C.在P点与Q点的速度大小之比
D.在P点与Q点的加速度大小之比
12.(2021·湖南·高考真题)2021年4月29日,中国空间站天和核心舱发射升空,准确进入预定轨道。根据任务安排,后续将发射问天实验舱和梦天实验舱,计划2022年完成空间站在轨建造。核心舱绕地球飞行的轨道可视为圆轨道,轨道离地面的高度约为地球半径的。下列说法正确的是( )
A.核心舱进入轨道后所受地球的万有引力大小约为它在地面时的倍
B.核心舱在轨道上飞行的速度大于
C.核心舱在轨道上飞行的周期小于
D.后续加挂实验舱后,空间站由于质量增大,轨道半径将变小
三、解答题(本大题共6小题)
13.(2021·福建·高考真题)天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,试推算这个双星系统的总质量.(引力常量为G)
14.(2021·上海·高考真题)宇航员在地球表面以一定初速度竖直向上抛出一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处.(取地球表面重力加速度g=10m/s2,空气阻力不计)
(1)求该星球表面附近的重力加速度g';
(2)已知该星球的半径与地球半径之比为R星∶R地=1∶4,求该星球的质量与地球质量之比M星∶M地.
15.(2020·全国·高考真题)如图所示,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油.假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原竖直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.
(1)设球形空腔体积为V,球心深度为d(远小于地球半径),求空腔所引起的Q点处的重力加速度反常;
(2)若在水平地面上半径为L的范围内发现:重力加速度反常值在δ与kδ(k>1)之间变化,且重力加速度反常的最大值出现在半径为L的范围的中心.如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积.
16.(2020·山东·高考真题)如图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。
(1)求两星球做圆周运动的周期。
(2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行为的周期记为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期T2。已知地球和月球的质量分别为5.98×1024kg和7.35×1022kg 。求T2与T1两者平方之比。(结果保留3位小数)
17.(2020·安徽·高考真题)(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即,k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知引力常量为G,太阳的质量为M太.
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立.经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质量M地.(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
18.(2020·安徽·高考真题)由三颗星体构成的系统,忽略其他星体对它们的影响,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做角速度相同的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况)若A星体的质量为2m,B、C两星体的质量均为m,三角形的边长为a,万有引力常量G已知,求:
(1)A星体所受合力的大小FA;
(2)B星体所受合力的大小FB;
(3)C星体的轨道半径RC;
(4)三星体做圆周运动的周期T。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
A.因发射的卫星要能变轨到绕太阳转动,则发射速度要大于第二宇宙速度,即发射速度介于11.2km/s与16.7km/s之间,故A错误;
B.因P点转移到Q点的转移轨道的半长轴大于地球公转轨道半径,则其周期大于地球公转周期(1年共12个月),则从P点转移到Q点的时间为轨道周期的一半时间应大于6个月,故B错误;
C.因在环绕火星的停泊轨道的半长轴小于调相轨道的半长轴,则由开普勒第三定律可知在环绕火星的停泊轨道运行的周期比在调相轨道上小,故C正确;
D.卫星从P点变轨时,要加速增大速度,此后做离心运动速度减小,则在地火转移轨道运动时的速度P点速度大于地球绕太阳的速度,故D错误;
故选C。
2.B
【解析】
AB.第一宇宙速度是指绕地球表面做圆周运动的速度,是环绕地球做圆周运动的所有卫星的最大环绕速度,该卫星的运转半径远大于地球的半径,可知运行线速度小于第一宇宙速度,选项A错误B正确;
CD.根据
可知
因为该卫星的运动周期与地球自转周期相同,等于“静止”在赤道上空的同步卫星的周期,可知该卫星的轨道半径等于“静止”在赤道上空的同步卫星的轨道半径,选项CD错误。
故选B。
3.D
【解析】
A. 设地球和火星的公转周期分别为T1、T2 ,轨道半径分别为r1、r2,由开普勒第三定律可得
可求得地球与火星的轨道半径之比,由太阳的引力提供向心力,则有
得
即地球与火星的线速度之比可以求得,但由于地球与火星的质量关系未知,因此不能求得地球与火星的动能之比,A错误;
B.则有地球和火星的角速度分别为
由题意知火星和地球每隔约26个月相距最近一次,又火星的轨道半径大于地球的轨道半径,则
由以上可解得
月
则地球与火星绕太阳的公转周期之比
T1∶T2 =7∶13
但不能求出两星球自转周期之比,B错误;
C.由物体在地球和火星表面的重力等于各自对物体的引力,则有
得
由于地球和火星的质量关系以及半径关系均未知,则两星球表面重力加速度的关系不可求,C错误;
D.地球与火星绕太阳运动的向心加速度由太阳对地球和火星的引力产生,所以向心加速度大小则有
得
由于两星球的轨道半径之比已知,则地球与火星绕太阳运动的向心加速度之比可以求得,D正确。
故选D。
4.D
【解析】
A.天问一号探测器在轨道Ⅱ上做变速圆周运动,受力不平衡,故A错误;
B.根据开普勒第三定律可知,轨道Ⅰ的半径大于轨道Ⅱ的半长轴,故在轨道Ⅰ运行周期比在Ⅱ时长,故B错误;
C.天问一号探测器从轨道Ⅰ进入Ⅱ,做近心运动,需要的向心力要小于提供的向心力,故要在P点点火减速,故C错误;
D.在轨道Ⅰ向P飞近时,万有引力做正功,动能增大,故速度增大,故D正确。
故选D。
5.B
【解析】
悬停时所受平台的作用力等于万有引力,根据
可得
故选B。
6.B
【解析】
可以近似把S2看成匀速圆周运动,由图可知,S2绕黑洞的周期T=16年,地球的公转周期T0=1年,S2绕黑洞做圆周运动的半径r与地球绕太阳做圆周运动的半径R关系是
地球绕太阳的向心力由太阳对地球的引力提供,由向心力公式可知
解得太阳的质量为
同理S2绕黑洞的向心力由黑洞对它的万有引力提供,由向心力公式可知
解得黑洞的质量为
综上可得
故选B。
7.D
【解析】
AB.卫星贴近地面做匀速圆周运动的线速度大小设为v1,此速度为第一宇宙速度,即v1=7.9km/s;地球半径约为6400km,则空间站离地高度在418km~421km之间。由
,
解得
空间站距离地面的最小高度约为h=418km<R=6400km,则
所以空间站绕地运行速度
故AB错误;
C.在4月份轨道半径出现明显的变大,则可知,机械能不守恒,故C错误;
D.在5月份轨道半径基本不变,故可视为机械能守恒,故D正确。
故选D。
8.C
【解析】
忽略火星自转则
①
可知
设与为1.8×105s的椭圆形停泊轨道周期相同的圆形轨道半径为,由万引力提供向心力可知
②
设近火点到火星中心为
③
设远火点到火星中心为
④
由开普勒第三定律可知
⑤
由以上分析可得
故选C。
9.AD
【解析】
A.根据密度的定义有
体积
可知火星的平均密度与月球的平均密度之比为
即火星的平均密度是月球的倍,故A正确;
BC.由
可知火星的重力加速度与月球表面的重力加速度之比为
即火星的重力加速度是月球表面的重力加速度的,由
可知火星的第一宇宙速度与月球的第一宇宙速度之比为
故BC错误;
D.由万有引力定律
可知火星对“祝融号”引力大小与月球对“玉兔二号”引力大小之比为
即火星对“祝融号”引力大小是月球对“玉兔二号”引力大小的倍,故D正确。
故选AD。
10.CD
【解析】
AC.根据开普勒第二定律,可知近地点的速度比远地点的速度大,则从P到Q阶段,万有引力对做负功,速率逐渐变小,所以从P到M所用的时间小于,A错误;C正确;
B.由于只有万有引力做功,从Q到N阶段,机械能保持不变,B正确;
D.从M到Q阶段,万有引力对它做负功,从Q到N阶段,万有引力做正功,D正确。
故选CD。
11.BCD
【解析】
A.设椭圆的长轴为2a,两焦点的距离为2c,则偏心率
且由题知,Q与O的距离约为,即
由此可得出a与c,由于是围绕致密天体运动,根据万有定律,可知无法求出两者的质量之比,故A错误;
B.根据开普勒第三定律有
式中k是与中心天体的质量M有关,且与M成正比;所以,对是围绕致密天体运动有
对地球围绕太阳运动有
两式相比,可得
因的半长轴a、周期,日地之间的距离,地球围绕太阳运动的周期都已知,故由上式,可以求出银河系中心致密天体与太阳的质量之比,故B正确;
C.根据开普勒第二定律有
解得
因a、c已求出,故可以求出在P点与Q点的速度大小之比,故C正确;
D.不管是在P点,还是在Q点,都只受致密天体的万有引力作用,根据牛顿第二定律有
解得
因P点到O点的距离为a+c,,Q点到O点的距离为a-c,解得
因a、c已求出,故在P点与Q点的加速度大小之比,故D正确。
故选BCD。
12.AC
【解析】
A.根据万有引力定律有
核心舱进入轨道后的万有引力与地面上万有引力之比为
所以A正确;
B.核心舱在轨道上飞行的速度小于7.9km/s,因为第一宇宙速度是最大的环绕速度,所以B错误;
C.根据
可知轨道半径越大周期越大,则其周期比同步卫星的周期小,小于24h,所以C正确;
D.卫星做圆周运动时万有引力提供向心力有
解得
则卫星的环绕速度与卫星的质量无关,所以变轨时需要点火减速或者点火加速,增加质量不会改变轨道半径,所以D错误;
故选AC。
【点睛】
13.
【解析】
设两颗恒星的质量分别为m1、m2,做圆周运动的半径分别为r1、r2,角速度分别为w1,w2.根据题意有
w1=w2 ① (1分)
r1+r2=r ② (1分)
根据万有引力定律和牛顿定律,有
G ③ (3分)
G ④ (3分)
联立以上各式解得
⑤ (2分)
根据解速度与周期的关系知
⑥ (2分)
联立③⑤⑥式解得
(3分)
本题考查天体运动中的双星问题,两星球间的相互作用力提供向心力,周期和角速度相同,由万有引力提供向心力列式求解
14.(1)2 m/s2 (2)1:80
【解析】
试题分析:运用运动学公式求出时间t与初速度之间的关系,求出地球表面重力加速度g与星球表面附近的重力加速度g′间的关系.根据万有引力等于重力表示出质量,求出星球的质量与地球质量之比.
(1)根据匀变速直线运动规律t=得:
从竖直上抛到最高点,上升的时间是=,上升和下降的时间相等,
所以从上抛到落回原处t=①
由于在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处.
根据匀变速直线运动规律得:
5t=②
由①②得星球表面附近的重力加速度g′=g=2m/s2,
(2)根据万有引力等于重力得::=mg
M=
所以==
15.(1) (2)
【解析】
(1)如果将近地表的球形空腔填满密度为ρ的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常可通过填充后的球形区域产生的附加引力来计算,
mΔg①
式中m是Q点处某质点的质量,M是填充后球形区域的质量.M=ρV②
而r是球形空腔中心O至Q点的距离r=③
Δg在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小 Q点处重力加速度改变的方向沿OQ方向,重力加速度反常Δg′是这一改变在竖直方向上的投影
Δg′=Δg④
联立①②③④式得Δg′=⑤
(2)由⑤式得,重力加速度反常Δg′的最大值和最小值分别为
(Δg′)max=⑥
(Δg′)min=⑦
由题设有(Δg′)max=kδ,(Δg′)min=δ⑧
联立⑥⑦⑧式得,地下球形空腔球心的深度和空腔的体积分别为
16.(1);(2)1.01
【解析】
试题分析:(1)A和B绕O做匀速圆周运动,它们之间的万有引力提供向心力,则A和B的向心力大小相等,且A和B和O始终共线,说明A和B有相同的角速度和周期,因此有:
联立解得:
对A根据牛顿第二定律和万有引力定律得:
化简得:
(2)将地月看成双星,由(1)得
将月球看作绕地心做圆周运动,根据牛顿第二定律和万有引力定律得:
化简得:
所以两种周期的平方比值为:
考点:考查了万有引力定律的应用
【点睛】
这是一个双星的问题,A和B绕O做匀速圆周运动,它们之间的万有引力提供各自的向心力,
A和B有相同的角速度和周期,结合牛顿第二定律和万有引力定律解决问题。
17.(1)(2)M地=6×1024kg
【解析】
(1)因行星绕太阳作匀速圆周运动,于是轨道的半长轴a即为轨道半径r.根据万有引力定律和牛顿第二定律有
①--------(3分)
于是有 ②--------(1分)
即 ③--------(1分)
(2)在月地系统中,设月球绕地球运动的轨道半径为R,周期为T,由②式可得
④--------(3分)
解得 M地=6×1024kg( M地=5×1024kg也算对 ) ⑤--------(2分)
18.(1) (2) (3) (4)
【解析】
(1)由万有引力定律,A星体所受B、C星体引力大小为
,
则合力大小为
(2)同上,B星体所受A、C星体引力大小分别为
则合力大小为
.
可得
(3)通过分析可知,圆心O在中垂线AD的中点,
(4)三星体运动周期相同,对C星体,由
可得
答案第1页,共2页
答案第1页,共2页
一、单选题(本大题共8小题)
1.(2021·浙江·高考真题)“天问一号”从地球发射后,在如图甲所示的P点沿地火转移轨道到Q点,再依次进入如图乙所示的调相轨道和停泊轨道,则天问一号( )
A.发射速度介于7.9km/s与11.2km/s之间
B.从P点转移到Q点的时间小于6个月
C.在环绕火星的停泊轨道运行的周期比在调相轨道上小
D.在地火转移轨道运动时的速度均大于地球绕太阳的速度
2.(2021·江苏·高考真题)我国航天人发扬“两弹一星”精神砥砺前行,从“东方红一号”到“北斗”不断创造奇迹。“北斗”第49颗卫星的发射迈出组网的关键一步。该卫星绕地球做圆周运动,运动周期与地球自转周期相同,轨道平面与地球赤道平面成一定夹角。该卫星( )
A.运动速度大于第一宇宙速度
B.运动速度小于第一宇宙速度
C.轨道半径大于“静止”在赤道上空的同步卫星
D.轨道半径小于“静止”在赤道上空的同步卫星
3.(2021·湖北·高考真题)2021年5月,天问一号探测器软着陆火星取得成功,迈出了我国星际探测征程的重要一步。火星与地球公转轨道近似为圆,两轨道平面近似重合,且火星与地球公转方向相同。火星与地球每隔约26个月相距最近,地球公转周期为12个月。由以上条件可以近似得出( )
A.地球与火星的动能之比
B.地球与火星的自转周期之比
C.地球表面与火星表面重力加速度大小之比
D.地球与火星绕太阳运动的向心加速度大小之比
4.(2021·天津·高考真题)2021年5月15日,天问一号探测器着陆火星取得成功,迈出了我国星际探测征程的重要一步,在火星上首次留下国人的印迹。天问一号探测器成功发射后,顺利被火星捕获,成为我国第一颗人造火星卫星。经过轨道调整,探测器先沿椭圆轨道Ⅰ运行,之后进入称为火星停泊轨道的椭圆轨道Ⅱ运行,如图所示,两轨道相切于近火点P,则天问一号探测器( )
A.在轨道Ⅱ上处于受力平衡状态 B.在轨道Ⅰ运行周期比在Ⅱ时短
C.从轨道Ⅰ进入Ⅱ在P处要加速 D.沿轨道Ⅰ向P飞近时速度增大
5.(2021·山东·高考真题)从“玉兔”登月到“祝融”探火,我国星际探测事业实现了由地月系到行星际的跨越。已知火星质量约为月球的9倍,半径约为月球的2倍,“祝融”火星车的质量约为“玉兔”月球车的2倍。在着陆前,“祝融”和“玉兔”都会经历一个由着陆平台支撑的悬停过程。悬停时,“祝融”与“玉兔”所受陆平台的作用力大小之比为( )
A.9∶1 B.9∶2 C.36∶1 D.72∶1
6.(2021·全国·高考真题)科学家对银河系中心附近的恒星S2进行了多年的持续观测,给出1994年到2002年间S2的位置如图所示。科学家认为S2的运动轨迹是半长轴约为(太阳到地球的距离为)的椭圆,银河系中心可能存在超大质量黑洞。这项研究工作获得了2020年诺贝尔物理学奖。若认为S2所受的作用力主要为该大质量黑洞的引力,设太阳的质量为M,可以推测出该黑洞质量约为( )
A. B. C. D.
7.(2021·浙江·高考真题)空间站在地球外层的稀薄大气中绕行,因气体阻力的影响,轨道高度会发生变化。空间站安装有发动机,可对轨道进行修正。图中给出了国际空间站在2020.02-2020.08期间离地高度随时间变化的曲线,则空间站( )
A.绕地运行速度约为
B.绕地运行速度约为
C.在4月份绕行的任意两小时内机械能可视为守恒
D.在5月份绕行的任意两小时内机械能可视为守恒
8.(2021·全国·高考真题)2021年2月,执行我国火星探测任务的“天问一号”探测器在成功实施三次近火制动后,进入运行周期约为1.8×105s的椭圆形停泊轨道,轨道与火星表面的最近距离约为2.8×105m。已知火星半径约为3.4×106m,火星表面处自由落体的加速度大小约为3.7m/s2,则“天问一号”的停泊轨道与火星表面的最远距离约为( )
A.6×105m B.6×106m C.6×107m D.6×108m
二、多选题(本大题共4小题)
9.(2021·重庆·高考真题)2021年5月15日“祝融号”火星车成功着陆火星表面,是我国航天事业发展中具有里程碑意义的进展。此前我国“玉兔二号”月球车首次实现月球背面软着陆,若“祝融号”的质量是“玉兔二号”的K倍,火星的质量是月球的N倍,火星的半径是月球的P倍,火星与月球均视为球体,则( )
A.火星的平均密度是月球的倍
B.火星的第一宇宙速度是月球的倍
C.火星的重力加速度大小是月球表面的倍
D.火星对“祝融号”引力的大小是月球对“玉兔二号”引力的倍
10.(2021·全国·高考真题)如图,海王星绕太阳沿椭圆轨道运动,P为近日点,Q为远日点,为轨道短轴的两个端点,运行的周期为。若只考虑海王星和太阳之间的相互作用,则海王星在从P经到N的运动过程中( )
A.从P到M所用的时间等于
B.从Q到N阶段,机械能逐渐变大
C.从P到Q阶段,速率逐渐变小
D.从M到N阶段,万有引力对它先做负功后做正功
11.(2021·福建·高考真题)两位科学家因为在银河系中心发现了一个超大质量的致密天体而获得了2020年诺贝尔物理学奖。他们对一颗靠近银河系中心的恒星的位置变化进行了持续观测,记录到的的椭圆轨道如图所示。图中O为椭圆的一个焦点,椭圆偏心率(离心率)约为0.87。P、Q分别为轨道的远银心点和近银心点,Q与O的距离约为(太阳到地球的距离为),的运行周期约为16年。假设的运动轨迹主要受银河系中心致密天体的万有引力影响,根据上述数据及日常的天文知识,可以推出( )
A.与银河系中心致密天体的质量之比
B.银河系中心致密天体与太阳的质量之比
C.在P点与Q点的速度大小之比
D.在P点与Q点的加速度大小之比
12.(2021·湖南·高考真题)2021年4月29日,中国空间站天和核心舱发射升空,准确进入预定轨道。根据任务安排,后续将发射问天实验舱和梦天实验舱,计划2022年完成空间站在轨建造。核心舱绕地球飞行的轨道可视为圆轨道,轨道离地面的高度约为地球半径的。下列说法正确的是( )
A.核心舱进入轨道后所受地球的万有引力大小约为它在地面时的倍
B.核心舱在轨道上飞行的速度大于
C.核心舱在轨道上飞行的周期小于
D.后续加挂实验舱后,空间站由于质量增大,轨道半径将变小
三、解答题(本大题共6小题)
13.(2021·福建·高考真题)天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星.双星系统在银河系中很普遍.利用双星系统中两颗恒星的运动特征可推算出它们的总质量.已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,试推算这个双星系统的总质量.(引力常量为G)
14.(2021·上海·高考真题)宇航员在地球表面以一定初速度竖直向上抛出一小球,经过时间t小球落回原处;若他在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处.(取地球表面重力加速度g=10m/s2,空气阻力不计)
(1)求该星球表面附近的重力加速度g';
(2)已知该星球的半径与地球半径之比为R星∶R地=1∶4,求该星球的质量与地球质量之比M星∶M地.
15.(2020·全国·高考真题)如图所示,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油.假定区域周围岩石均匀分布,密度为ρ;石油密度远小于ρ,可将上述球形区域视为空腔.如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏离.重力加速度在原竖直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”.为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象.已知引力常数为G.
(1)设球形空腔体积为V,球心深度为d(远小于地球半径),求空腔所引起的Q点处的重力加速度反常;
(2)若在水平地面上半径为L的范围内发现:重力加速度反常值在δ与kδ(k>1)之间变化,且重力加速度反常的最大值出现在半径为L的范围的中心.如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积.
16.(2020·山东·高考真题)如图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。
(1)求两星球做圆周运动的周期。
(2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行为的周期记为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期T2。已知地球和月球的质量分别为5.98×1024kg和7.35×1022kg 。求T2与T1两者平方之比。(结果保留3位小数)
17.(2020·安徽·高考真题)(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即,k是一个对所有行星都相同的常量.将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式.已知引力常量为G,太阳的质量为M太.
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立.经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质量M地.(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
18.(2020·安徽·高考真题)由三颗星体构成的系统,忽略其他星体对它们的影响,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做角速度相同的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况)若A星体的质量为2m,B、C两星体的质量均为m,三角形的边长为a,万有引力常量G已知,求:
(1)A星体所受合力的大小FA;
(2)B星体所受合力的大小FB;
(3)C星体的轨道半径RC;
(4)三星体做圆周运动的周期T。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【解析】
A.因发射的卫星要能变轨到绕太阳转动,则发射速度要大于第二宇宙速度,即发射速度介于11.2km/s与16.7km/s之间,故A错误;
B.因P点转移到Q点的转移轨道的半长轴大于地球公转轨道半径,则其周期大于地球公转周期(1年共12个月),则从P点转移到Q点的时间为轨道周期的一半时间应大于6个月,故B错误;
C.因在环绕火星的停泊轨道的半长轴小于调相轨道的半长轴,则由开普勒第三定律可知在环绕火星的停泊轨道运行的周期比在调相轨道上小,故C正确;
D.卫星从P点变轨时,要加速增大速度,此后做离心运动速度减小,则在地火转移轨道运动时的速度P点速度大于地球绕太阳的速度,故D错误;
故选C。
2.B
【解析】
AB.第一宇宙速度是指绕地球表面做圆周运动的速度,是环绕地球做圆周运动的所有卫星的最大环绕速度,该卫星的运转半径远大于地球的半径,可知运行线速度小于第一宇宙速度,选项A错误B正确;
CD.根据
可知
因为该卫星的运动周期与地球自转周期相同,等于“静止”在赤道上空的同步卫星的周期,可知该卫星的轨道半径等于“静止”在赤道上空的同步卫星的轨道半径,选项CD错误。
故选B。
3.D
【解析】
A. 设地球和火星的公转周期分别为T1、T2 ,轨道半径分别为r1、r2,由开普勒第三定律可得
可求得地球与火星的轨道半径之比,由太阳的引力提供向心力,则有
得
即地球与火星的线速度之比可以求得,但由于地球与火星的质量关系未知,因此不能求得地球与火星的动能之比,A错误;
B.则有地球和火星的角速度分别为
由题意知火星和地球每隔约26个月相距最近一次,又火星的轨道半径大于地球的轨道半径,则
由以上可解得
月
则地球与火星绕太阳的公转周期之比
T1∶T2 =7∶13
但不能求出两星球自转周期之比,B错误;
C.由物体在地球和火星表面的重力等于各自对物体的引力,则有
得
由于地球和火星的质量关系以及半径关系均未知,则两星球表面重力加速度的关系不可求,C错误;
D.地球与火星绕太阳运动的向心加速度由太阳对地球和火星的引力产生,所以向心加速度大小则有
得
由于两星球的轨道半径之比已知,则地球与火星绕太阳运动的向心加速度之比可以求得,D正确。
故选D。
4.D
【解析】
A.天问一号探测器在轨道Ⅱ上做变速圆周运动,受力不平衡,故A错误;
B.根据开普勒第三定律可知,轨道Ⅰ的半径大于轨道Ⅱ的半长轴,故在轨道Ⅰ运行周期比在Ⅱ时长,故B错误;
C.天问一号探测器从轨道Ⅰ进入Ⅱ,做近心运动,需要的向心力要小于提供的向心力,故要在P点点火减速,故C错误;
D.在轨道Ⅰ向P飞近时,万有引力做正功,动能增大,故速度增大,故D正确。
故选D。
5.B
【解析】
悬停时所受平台的作用力等于万有引力,根据
可得
故选B。
6.B
【解析】
可以近似把S2看成匀速圆周运动,由图可知,S2绕黑洞的周期T=16年,地球的公转周期T0=1年,S2绕黑洞做圆周运动的半径r与地球绕太阳做圆周运动的半径R关系是
地球绕太阳的向心力由太阳对地球的引力提供,由向心力公式可知
解得太阳的质量为
同理S2绕黑洞的向心力由黑洞对它的万有引力提供,由向心力公式可知
解得黑洞的质量为
综上可得
故选B。
7.D
【解析】
AB.卫星贴近地面做匀速圆周运动的线速度大小设为v1,此速度为第一宇宙速度,即v1=7.9km/s;地球半径约为6400km,则空间站离地高度在418km~421km之间。由
,
解得
空间站距离地面的最小高度约为h=418km<R=6400km,则
所以空间站绕地运行速度
故AB错误;
C.在4月份轨道半径出现明显的变大,则可知,机械能不守恒,故C错误;
D.在5月份轨道半径基本不变,故可视为机械能守恒,故D正确。
故选D。
8.C
【解析】
忽略火星自转则
①
可知
设与为1.8×105s的椭圆形停泊轨道周期相同的圆形轨道半径为,由万引力提供向心力可知
②
设近火点到火星中心为
③
设远火点到火星中心为
④
由开普勒第三定律可知
⑤
由以上分析可得
故选C。
9.AD
【解析】
A.根据密度的定义有
体积
可知火星的平均密度与月球的平均密度之比为
即火星的平均密度是月球的倍,故A正确;
BC.由
可知火星的重力加速度与月球表面的重力加速度之比为
即火星的重力加速度是月球表面的重力加速度的,由
可知火星的第一宇宙速度与月球的第一宇宙速度之比为
故BC错误;
D.由万有引力定律
可知火星对“祝融号”引力大小与月球对“玉兔二号”引力大小之比为
即火星对“祝融号”引力大小是月球对“玉兔二号”引力大小的倍,故D正确。
故选AD。
10.CD
【解析】
AC.根据开普勒第二定律,可知近地点的速度比远地点的速度大,则从P到Q阶段,万有引力对做负功,速率逐渐变小,所以从P到M所用的时间小于,A错误;C正确;
B.由于只有万有引力做功,从Q到N阶段,机械能保持不变,B正确;
D.从M到Q阶段,万有引力对它做负功,从Q到N阶段,万有引力做正功,D正确。
故选CD。
11.BCD
【解析】
A.设椭圆的长轴为2a,两焦点的距离为2c,则偏心率
且由题知,Q与O的距离约为,即
由此可得出a与c,由于是围绕致密天体运动,根据万有定律,可知无法求出两者的质量之比,故A错误;
B.根据开普勒第三定律有
式中k是与中心天体的质量M有关,且与M成正比;所以,对是围绕致密天体运动有
对地球围绕太阳运动有
两式相比,可得
因的半长轴a、周期,日地之间的距离,地球围绕太阳运动的周期都已知,故由上式,可以求出银河系中心致密天体与太阳的质量之比,故B正确;
C.根据开普勒第二定律有
解得
因a、c已求出,故可以求出在P点与Q点的速度大小之比,故C正确;
D.不管是在P点,还是在Q点,都只受致密天体的万有引力作用,根据牛顿第二定律有
解得
因P点到O点的距离为a+c,,Q点到O点的距离为a-c,解得
因a、c已求出,故在P点与Q点的加速度大小之比,故D正确。
故选BCD。
12.AC
【解析】
A.根据万有引力定律有
核心舱进入轨道后的万有引力与地面上万有引力之比为
所以A正确;
B.核心舱在轨道上飞行的速度小于7.9km/s,因为第一宇宙速度是最大的环绕速度,所以B错误;
C.根据
可知轨道半径越大周期越大,则其周期比同步卫星的周期小,小于24h,所以C正确;
D.卫星做圆周运动时万有引力提供向心力有
解得
则卫星的环绕速度与卫星的质量无关,所以变轨时需要点火减速或者点火加速,增加质量不会改变轨道半径,所以D错误;
故选AC。
【点睛】
13.
【解析】
设两颗恒星的质量分别为m1、m2,做圆周运动的半径分别为r1、r2,角速度分别为w1,w2.根据题意有
w1=w2 ① (1分)
r1+r2=r ② (1分)
根据万有引力定律和牛顿定律,有
G ③ (3分)
G ④ (3分)
联立以上各式解得
⑤ (2分)
根据解速度与周期的关系知
⑥ (2分)
联立③⑤⑥式解得
(3分)
本题考查天体运动中的双星问题,两星球间的相互作用力提供向心力,周期和角速度相同,由万有引力提供向心力列式求解
14.(1)2 m/s2 (2)1:80
【解析】
试题分析:运用运动学公式求出时间t与初速度之间的关系,求出地球表面重力加速度g与星球表面附近的重力加速度g′间的关系.根据万有引力等于重力表示出质量,求出星球的质量与地球质量之比.
(1)根据匀变速直线运动规律t=得:
从竖直上抛到最高点,上升的时间是=,上升和下降的时间相等,
所以从上抛到落回原处t=①
由于在某星球表面以相同的初速度竖直上抛同一小球,需经过时间5t小球落回原处.
根据匀变速直线运动规律得:
5t=②
由①②得星球表面附近的重力加速度g′=g=2m/s2,
(2)根据万有引力等于重力得::=mg
M=
所以==
15.(1) (2)
【解析】
(1)如果将近地表的球形空腔填满密度为ρ的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常可通过填充后的球形区域产生的附加引力来计算,
mΔg①
式中m是Q点处某质点的质量,M是填充后球形区域的质量.M=ρV②
而r是球形空腔中心O至Q点的距离r=③
Δg在数值上等于由于存在球形空腔所引起的Q点处重力加速度改变的大小 Q点处重力加速度改变的方向沿OQ方向,重力加速度反常Δg′是这一改变在竖直方向上的投影
Δg′=Δg④
联立①②③④式得Δg′=⑤
(2)由⑤式得,重力加速度反常Δg′的最大值和最小值分别为
(Δg′)max=⑥
(Δg′)min=⑦
由题设有(Δg′)max=kδ,(Δg′)min=δ⑧
联立⑥⑦⑧式得,地下球形空腔球心的深度和空腔的体积分别为
16.(1);(2)1.01
【解析】
试题分析:(1)A和B绕O做匀速圆周运动,它们之间的万有引力提供向心力,则A和B的向心力大小相等,且A和B和O始终共线,说明A和B有相同的角速度和周期,因此有:
联立解得:
对A根据牛顿第二定律和万有引力定律得:
化简得:
(2)将地月看成双星,由(1)得
将月球看作绕地心做圆周运动,根据牛顿第二定律和万有引力定律得:
化简得:
所以两种周期的平方比值为:
考点:考查了万有引力定律的应用
【点睛】
这是一个双星的问题,A和B绕O做匀速圆周运动,它们之间的万有引力提供各自的向心力,
A和B有相同的角速度和周期,结合牛顿第二定律和万有引力定律解决问题。
17.(1)(2)M地=6×1024kg
【解析】
(1)因行星绕太阳作匀速圆周运动,于是轨道的半长轴a即为轨道半径r.根据万有引力定律和牛顿第二定律有
①--------(3分)
于是有 ②--------(1分)
即 ③--------(1分)
(2)在月地系统中,设月球绕地球运动的轨道半径为R,周期为T,由②式可得
④--------(3分)
解得 M地=6×1024kg( M地=5×1024kg也算对 ) ⑤--------(2分)
18.(1) (2) (3) (4)
【解析】
(1)由万有引力定律,A星体所受B、C星体引力大小为
,
则合力大小为
(2)同上,B星体所受A、C星体引力大小分别为
则合力大小为
.
可得
(3)通过分析可知,圆心O在中垂线AD的中点,
(4)三星体运动周期相同,对C星体,由
可得
答案第1页,共2页
答案第1页,共2页
同课章节目录
