人教版六年级下学期数学第四单元4.2.2反比例课件(共21张PPT)
文档属性
| 名称 | 人教版六年级下学期数学第四单元4.2.2反比例课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 34.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 21:15:11 | ||
图片预览







文档简介
(共21张PPT)
反比例
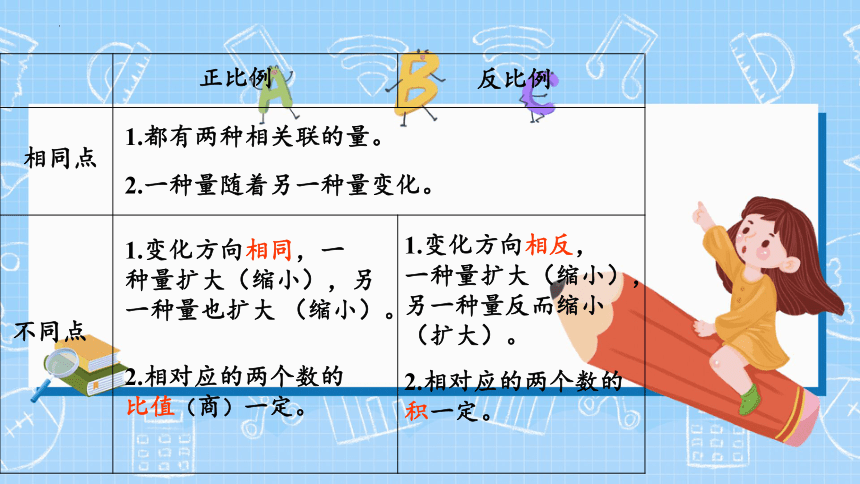
正比例
反比例
相同点
不同点
1.都有两种相关联的量。
2.一种量随着另一种量变化。
1.变化方向相同,一
种量扩大(缩小),另
一种量也扩大 (缩小)。
1.变化方向相反,
一种量扩大(缩小),另一种量反而缩小
(扩大)。
2.相对应的两个数的
比值(商)一定。
2.相对应的两个数的
积一定。
一种量变化,另一种量也
随着变化,
这两种量就叫做成正比例的量,
它们的关系叫做正比例关系。
两种相关联的量,
正比例的意义
如果这两种量中相对应的两个数的比值
(也就是商)一定,
把相同体积的水倒入底面积不同的杯子。
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
新课讲解
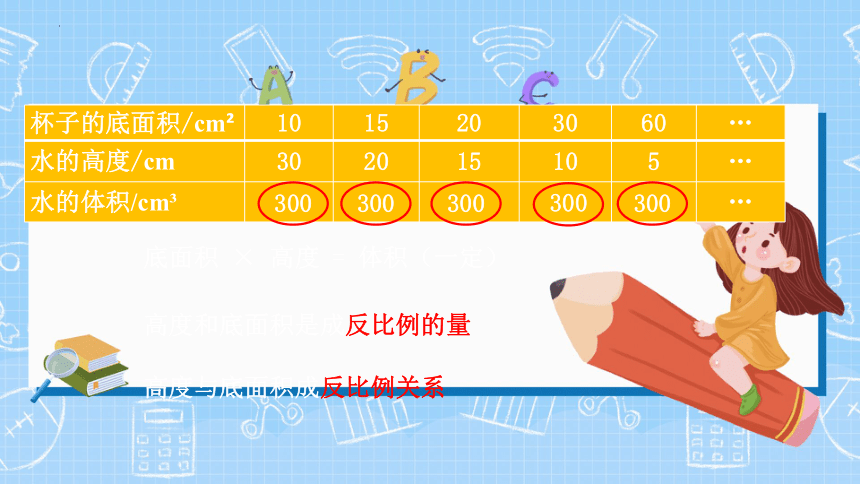
底面积 × 高度 = 体积(一定)
高度和底面积是成反比例的量
高度与底面积成反比例关系
杯子的底面积/cm 10 15 20 30 60 …
水的高度/cm 30 20 15 10 5 …
水的体积/cm …
300
300
300
300
300
杯子的底面积/cm 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
水的高度是怎样随着杯子底面积的大小变化而变化的?
底面积增加,高度减小。
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
底面积
高度
=
体积
×
新课讲解
请你判断下面两种量是否成反比例关系:
(1)如果路程一定,速度和时间。
(2)同一袋米,平均每天吃掉的米的数量和天数。
(3)六(1)班的人数一定,出勤人数和缺勤人数。
(4)铺地面积一定,每块方砖的 和块数。
(5)圆柱的底面积一定,体积和高。
成反比例
成反比例
不成反比例
成反比例
速度×时间=路程(一定)
出勤人数+缺勤人数=六(1)班总人数(一定)
平均每天吃掉的米的数量×天数=米的总量(一定)
边长
面积
每块方砖的面积×块数=铺地面积(一定)
1、成反比例的量有什么特征?
(1)、是两种相关联的量,一种量随着 另一种量变化。
(2)、变化方向相反, 一种量扩大(缩小)另一种量反而缩小(扩大)。
(3)、相对应的两个量的乘积是一定的。
xy=k(一定)
2、反比例关系式
速度×时间=路程(一定)
单价×数量=总价(一定)
底面积×高=体积(一定)
长×宽=长方形面积(一定)
一辆汽车行驶的时间和所行路程如下表。
时间(时)
路程(千米)
1
80
160
240
观察上表,回答下面的问题:
(1)表中有哪两个量?
(2)路程是怎样随着时间变化的?
(3)相对应的路程和时间的比
各是多少?比值是多少?
2
3
观察数据,你有什么发现
新课讲解
5.成反比例的两种量中,一种量扩大,另一种量 。
A.随着扩大
B随着.缩小
C.不变
D.不确定
6.成反比例的两种量变化的规律是它们的 不变。
A.和
B.差
C.积
D.商
7.一本书的总字数一定,每页字数与页数 。
A.成反比例
B.不成反比例
C.成正比例
D.不一定
8.三角形的面积一定,它的底和高 。
A.成反比例
B.不成反比例
C.成正比例
D.不一定
(B)
(C)
(A)
(A)
课堂游戏
一天,小蓝鱼正自由自在的游泳。突然,一条大鲨鱼游过来了,请你帮助小蓝鱼脱离危险。请你判断下列题目是否正确,如果判断正确则小鱼可以顺利避开鲨鱼,如果判断错误,小鱼就会被鲨鱼吃掉。
救救小鱼
用字母表示正比例的关系
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),比例关系可以用这样的式子表示:
哈哈哈,吃饱了!
修路的总米数一定,修好了的米数和剩下的米数成反比例。
练习本的本数和总价是两种相关联的量,本数增加,总价也随着( ),本数减少,总价也随着( ),这两种量中相对应的两个数的( )一定,也就是( )一定,练习本的本数和总价成( )关系。
增加
减少
比值
单价
正比例
说一说:这节课你有什么收获?
课后思考:在同一时间和同一地点,身高和影长成正比例吗?
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么?
每天运的吨数/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
300×1
150×2
100×3
=
=
=
300
货物的
总吨数
课堂总结:
1.反比例的意义
两种相关联的量
积一定
2.反比例的图象
曲线
3.反比例和正比例的相同点和不同点
感谢同学们积极配合!
反比例
正比例
反比例
相同点
不同点
1.都有两种相关联的量。
2.一种量随着另一种量变化。
1.变化方向相同,一
种量扩大(缩小),另
一种量也扩大 (缩小)。
1.变化方向相反,
一种量扩大(缩小),另一种量反而缩小
(扩大)。
2.相对应的两个数的
比值(商)一定。
2.相对应的两个数的
积一定。
一种量变化,另一种量也
随着变化,
这两种量就叫做成正比例的量,
它们的关系叫做正比例关系。
两种相关联的量,
正比例的意义
如果这两种量中相对应的两个数的比值
(也就是商)一定,
把相同体积的水倒入底面积不同的杯子。
杯子的底面积与水的高度的变化情况如下表。
杯子的底面积/cm
水的高度/cm
10
30
15
20
20
15
30
10
60
5
…
…
新课讲解
底面积 × 高度 = 体积(一定)
高度和底面积是成反比例的量
高度与底面积成反比例关系
杯子的底面积/cm 10 15 20 30 60 …
水的高度/cm 30 20 15 10 5 …
水的体积/cm …
300
300
300
300
300
杯子的底面积/cm 10 15 20 30 60 ...
水的高度/cm 30 20 15 10 5 ...
水的高度是怎样随着杯子底面积的大小变化而变化的?
底面积增加,高度减小。
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
底面积
高度
=
体积
×
新课讲解
请你判断下面两种量是否成反比例关系:
(1)如果路程一定,速度和时间。
(2)同一袋米,平均每天吃掉的米的数量和天数。
(3)六(1)班的人数一定,出勤人数和缺勤人数。
(4)铺地面积一定,每块方砖的 和块数。
(5)圆柱的底面积一定,体积和高。
成反比例
成反比例
不成反比例
成反比例
速度×时间=路程(一定)
出勤人数+缺勤人数=六(1)班总人数(一定)
平均每天吃掉的米的数量×天数=米的总量(一定)
边长
面积
每块方砖的面积×块数=铺地面积(一定)
1、成反比例的量有什么特征?
(1)、是两种相关联的量,一种量随着 另一种量变化。
(2)、变化方向相反, 一种量扩大(缩小)另一种量反而缩小(扩大)。
(3)、相对应的两个量的乘积是一定的。
xy=k(一定)
2、反比例关系式
速度×时间=路程(一定)
单价×数量=总价(一定)
底面积×高=体积(一定)
长×宽=长方形面积(一定)
一辆汽车行驶的时间和所行路程如下表。
时间(时)
路程(千米)
1
80
160
240
观察上表,回答下面的问题:
(1)表中有哪两个量?
(2)路程是怎样随着时间变化的?
(3)相对应的路程和时间的比
各是多少?比值是多少?
2
3
观察数据,你有什么发现
新课讲解
5.成反比例的两种量中,一种量扩大,另一种量 。
A.随着扩大
B随着.缩小
C.不变
D.不确定
6.成反比例的两种量变化的规律是它们的 不变。
A.和
B.差
C.积
D.商
7.一本书的总字数一定,每页字数与页数 。
A.成反比例
B.不成反比例
C.成正比例
D.不一定
8.三角形的面积一定,它的底和高 。
A.成反比例
B.不成反比例
C.成正比例
D.不一定
(B)
(C)
(A)
(A)
课堂游戏
一天,小蓝鱼正自由自在的游泳。突然,一条大鲨鱼游过来了,请你帮助小蓝鱼脱离危险。请你判断下列题目是否正确,如果判断正确则小鱼可以顺利避开鲨鱼,如果判断错误,小鱼就会被鲨鱼吃掉。
救救小鱼
用字母表示正比例的关系
如果用字母x和y表示两种相关联的量,用k表示它们的比值(一定),比例关系可以用这样的式子表示:
哈哈哈,吃饱了!
修路的总米数一定,修好了的米数和剩下的米数成反比例。
练习本的本数和总价是两种相关联的量,本数增加,总价也随着( ),本数减少,总价也随着( ),这两种量中相对应的两个数的( )一定,也就是( )一定,练习本的本数和总价成( )关系。
增加
减少
比值
单价
正比例
说一说:这节课你有什么收获?
课后思考:在同一时间和同一地点,身高和影长成正比例吗?
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说一说这个积表示什么?
每天运的吨数/t 300 150 100 75 60 50
运货的天数/天 1 2 3 4 5 6
300×1
150×2
100×3
=
=
=
300
货物的
总吨数
课堂总结:
1.反比例的意义
两种相关联的量
积一定
2.反比例的图象
曲线
3.反比例和正比例的相同点和不同点
感谢同学们积极配合!
