六年级下学期数学第五单元5数学广角-鸽巢问题课件(共20张PPT)
文档属性
| 名称 | 六年级下学期数学第五单元5数学广角-鸽巢问题课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 31.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 21:22:08 | ||
图片预览





文档简介
(共20张PPT)
数学广角-鸽巢问题
学习目标
理解“总有”“至少”的意义,理解“至少数=商+1”。
理解鸽巢原理,掌握先“平均分”,再调整的方法。
了解什么是鸽巢原理,学会简单的鸽巢原理分析方法。
鸽巢问题
活动内容: 将4支铅笔放进3个笔筒里。
活动目的: 无论怎样放,
总有一个笔筒里至少有( )支笔。
合作学习,展示交流
导学提示(一)
例2:把7本书放进6个抽屉中,可以怎么放?有几种情况?不管怎么放,总有一个抽屉至少放进几本书?为什么?
1、任务:探究抽屉原理
2、要求:
(1)自己动手在小组内摆一摆,画一画。
(2)小组内同学交流思考过程。
(3)你能用算式表示以上过程吗?你有什么发现?
(4)小组交流展示。
评价:活动认真的小组
新课讲解
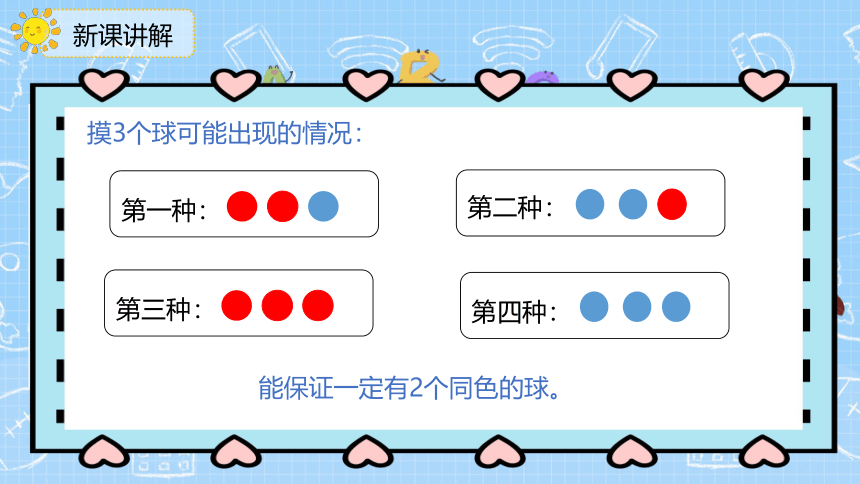
摸3个球可能出现的情况:
第一种:
第二种:
第三种:
第四种:
能保证一定有2个同色的球。
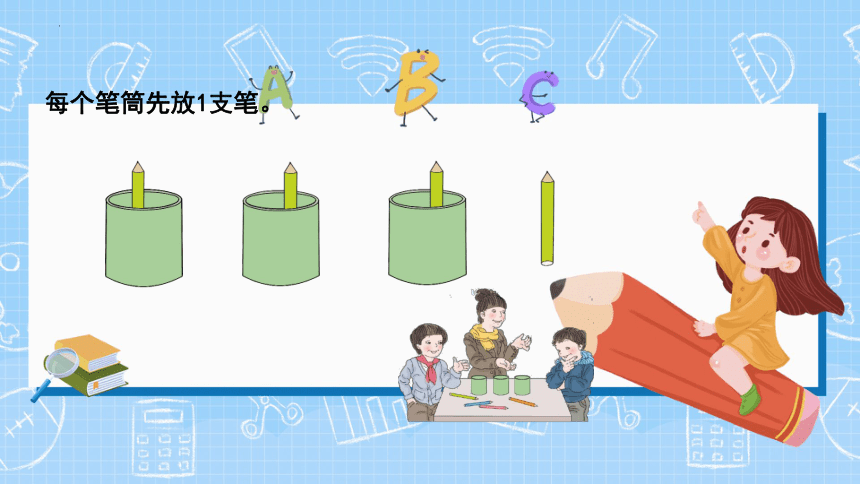
每个笔筒先放1支笔。
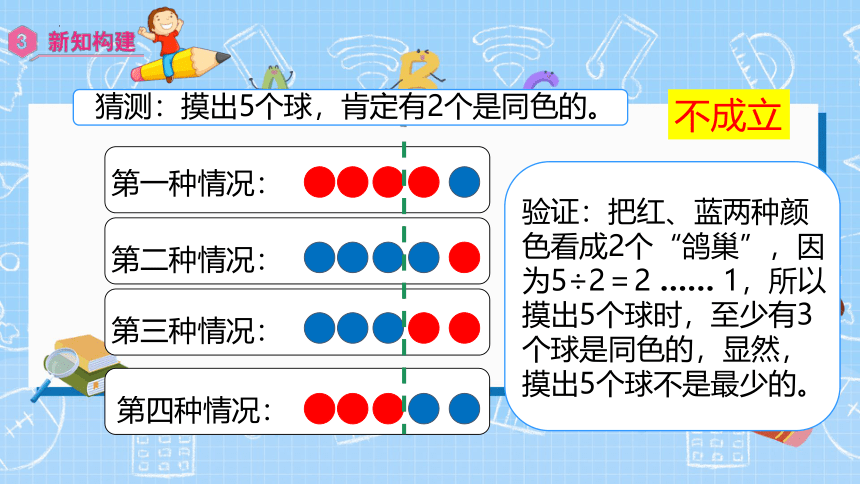
第一种情况:
第二种情况:
第三种情况:
第四种情况:
验证:把红、蓝两种颜色看成2个“鸽巢”,因为5÷2=2 …… 1,所以摸出5个球时,至少有3个球是同色的,显然,摸出5个球不是最少的。
猜测:摸出5个球,肯定有2个是同色的。
不成立
新课讲解
从两种颜色的球中保证摸出2个同色的,至少要摸出3个球。
要保证有一个抽屉至少有2个物体,分放的物体个数至少要比抽屉数多1。
要保证摸出两个同色的球,摸出的球的个数至少要比颜色种数多1。
教材第70页“做一做”第1题。
他们说得对吗?为什么?
向东小学六年级共有367名学生,其中六(2)班有49名学生。
六年级里至少有两人的生日是同一天。
六(2)班中至少有5人是同一个月出生的。
课堂练习
在一副扑克牌中,最少要抽取多少张,才能保证取出的牌中四种花色都有?
最不利的情形是:取出四种花色中的三种花色牌各13张,再加上2张王牌,这41张牌中没有四种花色。剩下的正好是另一种花色的13张牌,再抽一张,四种花色都有了。
13×3+2+1=42(张)
答:最少要取出42张,才能保证取出的牌中四种花色都有。
7只鸽子飞回5个鸽巢,至少有( )只鸽子要飞进同一个鸽巢里。
7÷5 = 1
……
2
1+1 = 2
基本练习
11只鸽子飞回4个鸽巢,总有一个鸽巢至少飞进了( )只鸽子。
11÷4 = 2
……
3
2+1 = 3
基本练习
例.把7本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进( )本书。为什么?
7÷3 = 2
……
1
2+1 = 3
8本呢?
8÷3 = 2
……
2
2+1 = 3
10本呢?
10÷3 = 3
……
1
3+1 = 4
把5支笔放进4个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔,为什么?
假设每个笔筒里先放1支笔,最多可放4支,剩下的1支还要放进其中一个笔筒里,不管怎么放,
总有一个笔筒里至少放进( 2 )支笔。
我能说
方法一
方法二
(3,0)
(2,1)
把3本书放进两个抽屉,有几种放法?
课堂小结
如果物体的个数除以抽屉数有余数,用所得的商加一,就会确定总有一个抽屉里至少放几个物体了。
课堂作业
1、随意找13位老师,他们中至少有2人的属相相同。为什么?
2、任意367名学生中,一定存在2名学生在同一天过生日。为什么?
感谢同学们积极配合!
数学广角-鸽巢问题
学习目标
理解“总有”“至少”的意义,理解“至少数=商+1”。
理解鸽巢原理,掌握先“平均分”,再调整的方法。
了解什么是鸽巢原理,学会简单的鸽巢原理分析方法。
鸽巢问题
活动内容: 将4支铅笔放进3个笔筒里。
活动目的: 无论怎样放,
总有一个笔筒里至少有( )支笔。
合作学习,展示交流
导学提示(一)
例2:把7本书放进6个抽屉中,可以怎么放?有几种情况?不管怎么放,总有一个抽屉至少放进几本书?为什么?
1、任务:探究抽屉原理
2、要求:
(1)自己动手在小组内摆一摆,画一画。
(2)小组内同学交流思考过程。
(3)你能用算式表示以上过程吗?你有什么发现?
(4)小组交流展示。
评价:活动认真的小组
新课讲解
摸3个球可能出现的情况:
第一种:
第二种:
第三种:
第四种:
能保证一定有2个同色的球。
每个笔筒先放1支笔。
第一种情况:
第二种情况:
第三种情况:
第四种情况:
验证:把红、蓝两种颜色看成2个“鸽巢”,因为5÷2=2 …… 1,所以摸出5个球时,至少有3个球是同色的,显然,摸出5个球不是最少的。
猜测:摸出5个球,肯定有2个是同色的。
不成立
新课讲解
从两种颜色的球中保证摸出2个同色的,至少要摸出3个球。
要保证有一个抽屉至少有2个物体,分放的物体个数至少要比抽屉数多1。
要保证摸出两个同色的球,摸出的球的个数至少要比颜色种数多1。
教材第70页“做一做”第1题。
他们说得对吗?为什么?
向东小学六年级共有367名学生,其中六(2)班有49名学生。
六年级里至少有两人的生日是同一天。
六(2)班中至少有5人是同一个月出生的。
课堂练习
在一副扑克牌中,最少要抽取多少张,才能保证取出的牌中四种花色都有?
最不利的情形是:取出四种花色中的三种花色牌各13张,再加上2张王牌,这41张牌中没有四种花色。剩下的正好是另一种花色的13张牌,再抽一张,四种花色都有了。
13×3+2+1=42(张)
答:最少要取出42张,才能保证取出的牌中四种花色都有。
7只鸽子飞回5个鸽巢,至少有( )只鸽子要飞进同一个鸽巢里。
7÷5 = 1
……
2
1+1 = 2
基本练习
11只鸽子飞回4个鸽巢,总有一个鸽巢至少飞进了( )只鸽子。
11÷4 = 2
……
3
2+1 = 3
基本练习
例.把7本书放进3个抽屉,不管怎么放,总有一个抽屉至少放进( )本书。为什么?
7÷3 = 2
……
1
2+1 = 3
8本呢?
8÷3 = 2
……
2
2+1 = 3
10本呢?
10÷3 = 3
……
1
3+1 = 4
把5支笔放进4个笔筒里,不管怎么放,总有一个笔筒里至少放进( )支笔,为什么?
假设每个笔筒里先放1支笔,最多可放4支,剩下的1支还要放进其中一个笔筒里,不管怎么放,
总有一个笔筒里至少放进( 2 )支笔。
我能说
方法一
方法二
(3,0)
(2,1)
把3本书放进两个抽屉,有几种放法?
课堂小结
如果物体的个数除以抽屉数有余数,用所得的商加一,就会确定总有一个抽屉里至少放几个物体了。
课堂作业
1、随意找13位老师,他们中至少有2人的属相相同。为什么?
2、任意367名学生中,一定存在2名学生在同一天过生日。为什么?
感谢同学们积极配合!
