人教版六年级下学期数学第六单元6.4数学思考课件(共22张PPT)
文档属性
| 名称 | 人教版六年级下学期数学第六单元6.4数学思考课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 28.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
数学思考
华罗庚
同学们,在解决数学难题时我们要学会化繁为简,知难而“退”, 要善于退,足够的退,退到最简单又不失关键的地方。那么,你就已经找到这道题的精髓了。
平面上有101个点,每两点连成一条线段,共能连成多少条不同的线段?趣味导入
曹冲称象 等量代换
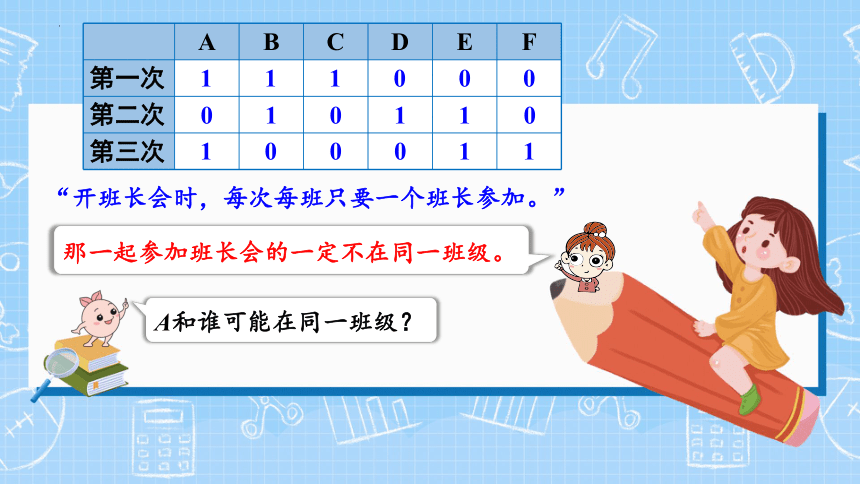
“开班长会时,每次每班只要一个班长参加。”
A B C D E F
第一次
第二次
第三次
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
那一起参加班长会的一定不在同一班级。
A和谁可能在同一班级?
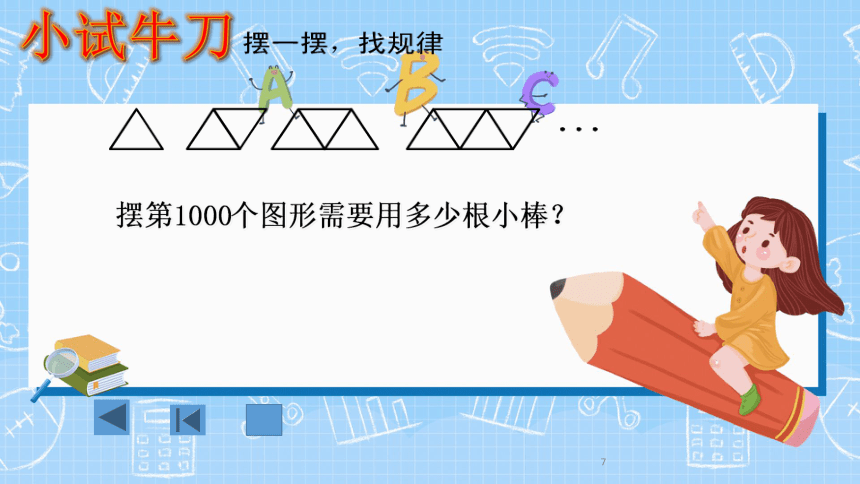
摆第1000个图形需要用多少根小棒?小试牛刀新知讲解
① ② ③
4×█=24
█=6
▲=█+█+█=18
也可以直接推理解决问题:丁叔叔不是工人,假设他是教师,即和王阿姨的职业相同,此时就和“只有刘阿姨和李叔叔的职业相同”产生矛盾,因此丁叔叔是军人。
王阿姨 丁叔叔 刘阿姨 李叔叔
工人
教师
军人
×
√
√
×
√
√
答:王阿姨是教师,丁叔叔是军人,刘阿姨和李叔叔都是工人。
数学思考数学思考
A
B
C
A
B
A
B
C
D
A
B
C
D
E
3个点连成线段的总条数:
4个点连成线段的总条数:
1+2+3
1+2
5个点连成线段的总条数:
1+2+3+4
总条数
增加条数
点数
2
1
3
2
3
4
3
6
5
4
10
6
5
6个点连成线段的总条数:
1+2+3+4+5
15
1.观察下图,想一想。
(2)*第n幅图有多少个棋子?
(1) (2) (3) (4)
……
每幅图的行数和列数都等于它的序号,n×n=n2(个),因此第n幅图有n2个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
新知讲解
将两种图形转化成一种图形
将▲换成█
7个点:1+2+3+4+5+6=21(条)
8个点:1+2+3+4+5+6+7=28(条)
12个点可以连多少条线段?20个点呢?
12个点:1+2+3+4+5+6+7+8+9+10
+11=66(条)
20个点:1+2+3+4+5+6+7+8+9+10+11+12
+13+14+15+16+17+18+19=190(条)
每两个球队进行一场比赛,一共要比赛多少场?
意大利
法国
加拿大
西班牙
英格兰
德国
俄罗斯
如图所示的三个图形都是用同样大小的三角形按一定规律拼成的一组图形。
…
(1)第5个图形中,有( )个白三角形。
21
第1个
第2个
第3个
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5+6=21
新知讲解
因为○+☆=160,◎+☆=160
所以(○+☆)-(◎+☆)=160-160
○+☆-◎-☆=160-160
○-◎=0-0
所以○=◎
a-(b+c)=a-b-c
有一个人每星期一、三、五说真话,二、四、六、日说假话。有一天他说:“我明天将说真话。”这天是星期几?
若这句话是星期一、三、五说的,那么是真话,第二天就应该说真话,与题目矛盾;如果这句话是星期二、四、日说的,就是假话,那么第二天说假话,也与题目矛盾;所以这句话只能是星期六说的,是假话,第二天星期日正好也说假话。
答:这天是星期六。
课堂练习
○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
(1)○+□=91 △+□=63 △+○=46
想一想
2○+2△+2□=91+63+46
2(○+△+□)=200
○+△+□=100
△=100-91=9
○=100-63=37
□=100-46=54
课堂练习
○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
(1)□-○=8 □+○=12 △=□+□+○
想一想
□-○+□-○=8+12
2个□=20
□=10
△=□+□+○=10+10+2=22
□=10 △=22 ○=2
课堂练习
如图,把三角形ABC的边长延长到点D。
(1)∠3和∠4拼成的是什么角?
(2)你能说明∠1+∠2=∠4吗?
想一想
(1)∠3和∠4拼成的是平角。
(2)因为∠1+∠2+∠3=180° ∠3+∠4=180°
所以 ∠1+∠2=180°-∠3
∠4=180°-∠3
所以∠1+∠2=∠4
说说你的感受吧……
感谢同学们积极配合!
数学思考
华罗庚
同学们,在解决数学难题时我们要学会化繁为简,知难而“退”, 要善于退,足够的退,退到最简单又不失关键的地方。那么,你就已经找到这道题的精髓了。
平面上有101个点,每两点连成一条线段,共能连成多少条不同的线段?趣味导入
曹冲称象 等量代换
“开班长会时,每次每班只要一个班长参加。”
A B C D E F
第一次
第二次
第三次
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
那一起参加班长会的一定不在同一班级。
A和谁可能在同一班级?
摆第1000个图形需要用多少根小棒?小试牛刀新知讲解
① ② ③
4×█=24
█=6
▲=█+█+█=18
也可以直接推理解决问题:丁叔叔不是工人,假设他是教师,即和王阿姨的职业相同,此时就和“只有刘阿姨和李叔叔的职业相同”产生矛盾,因此丁叔叔是军人。
王阿姨 丁叔叔 刘阿姨 李叔叔
工人
教师
军人
×
√
√
×
√
√
答:王阿姨是教师,丁叔叔是军人,刘阿姨和李叔叔都是工人。
数学思考数学思考
A
B
C
A
B
A
B
C
D
A
B
C
D
E
3个点连成线段的总条数:
4个点连成线段的总条数:
1+2+3
1+2
5个点连成线段的总条数:
1+2+3+4
总条数
增加条数
点数
2
1
3
2
3
4
3
6
5
4
10
6
5
6个点连成线段的总条数:
1+2+3+4+5
15
1.观察下图,想一想。
(2)*第n幅图有多少个棋子?
(1) (2) (3) (4)
……
每幅图的行数和列数都等于它的序号,n×n=n2(个),因此第n幅图有n2个棋子。
1个
4个
9个
16个
1×1
2×2
3×3
4×4
新知讲解
将两种图形转化成一种图形
将▲换成█
7个点:1+2+3+4+5+6=21(条)
8个点:1+2+3+4+5+6+7=28(条)
12个点可以连多少条线段?20个点呢?
12个点:1+2+3+4+5+6+7+8+9+10
+11=66(条)
20个点:1+2+3+4+5+6+7+8+9+10+11+12
+13+14+15+16+17+18+19=190(条)
每两个球队进行一场比赛,一共要比赛多少场?
意大利
法国
加拿大
西班牙
英格兰
德国
俄罗斯
如图所示的三个图形都是用同样大小的三角形按一定规律拼成的一组图形。
…
(1)第5个图形中,有( )个白三角形。
21
第1个
第2个
第3个
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5+6=21
新知讲解
因为○+☆=160,◎+☆=160
所以(○+☆)-(◎+☆)=160-160
○+☆-◎-☆=160-160
○-◎=0-0
所以○=◎
a-(b+c)=a-b-c
有一个人每星期一、三、五说真话,二、四、六、日说假话。有一天他说:“我明天将说真话。”这天是星期几?
若这句话是星期一、三、五说的,那么是真话,第二天就应该说真话,与题目矛盾;如果这句话是星期二、四、日说的,就是假话,那么第二天说假话,也与题目矛盾;所以这句话只能是星期六说的,是假话,第二天星期日正好也说假话。
答:这天是星期六。
课堂练习
○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
(1)○+□=91 △+□=63 △+○=46
想一想
2○+2△+2□=91+63+46
2(○+△+□)=200
○+△+□=100
△=100-91=9
○=100-63=37
□=100-46=54
课堂练习
○、□、△各代表一个数,根据下面的已知条件,求○、□、△的值。
(1)□-○=8 □+○=12 △=□+□+○
想一想
□-○+□-○=8+12
2个□=20
□=10
△=□+□+○=10+10+2=22
□=10 △=22 ○=2
课堂练习
如图,把三角形ABC的边长延长到点D。
(1)∠3和∠4拼成的是什么角?
(2)你能说明∠1+∠2=∠4吗?
想一想
(1)∠3和∠4拼成的是平角。
(2)因为∠1+∠2+∠3=180° ∠3+∠4=180°
所以 ∠1+∠2=180°-∠3
∠4=180°-∠3
所以∠1+∠2=∠4
说说你的感受吧……
感谢同学们积极配合!
