2021-2022人教版 数学 七年级下册 5.3.1 平行线的性质 课件(共24张)
文档属性
| 名称 | 2021-2022人教版 数学 七年级下册 5.3.1 平行线的性质 课件(共24张) |  | |
| 格式 | ppt | ||
| 文件大小 | 688.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 10:46:51 | ||
图片预览




文档简介
(共24张PPT)
5.3 平行线的性质
5.3.1 平行线的性质
根据右图,填空:
①如果∠1=∠C,
那么__∥__.( )
② 如果∠1=∠B ,
那么__∥__.( )
③ 如果∠2+∠B=180°,
那么__∥__.( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
E
A
C
D
B
1
2
3
4
1.经历探索平行线的性质的过程.
2.掌握平行线的性质并能够灵活应用.
3.综合运用平行线的判定与性质解决问题.
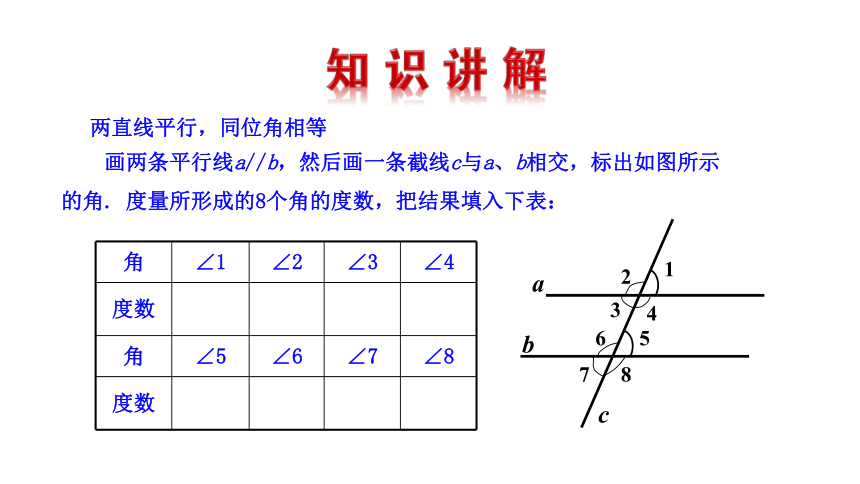
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
1
2
a
c
5
6
7
8
3
4
两直线平行,同位角相等
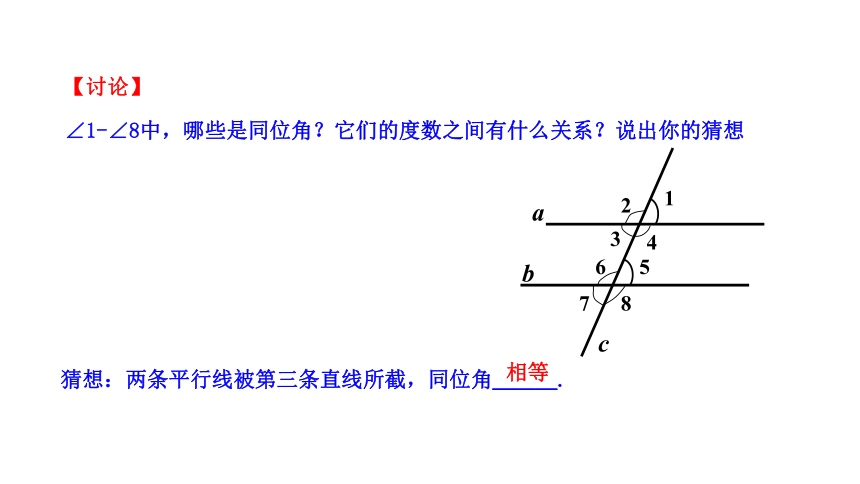
【讨论】
∠1-∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想
猜想:两条平行线被第三条直线所截,同位角___.
相等
b
1
2
a
c
5
6
7
8
3
4
a
b
d
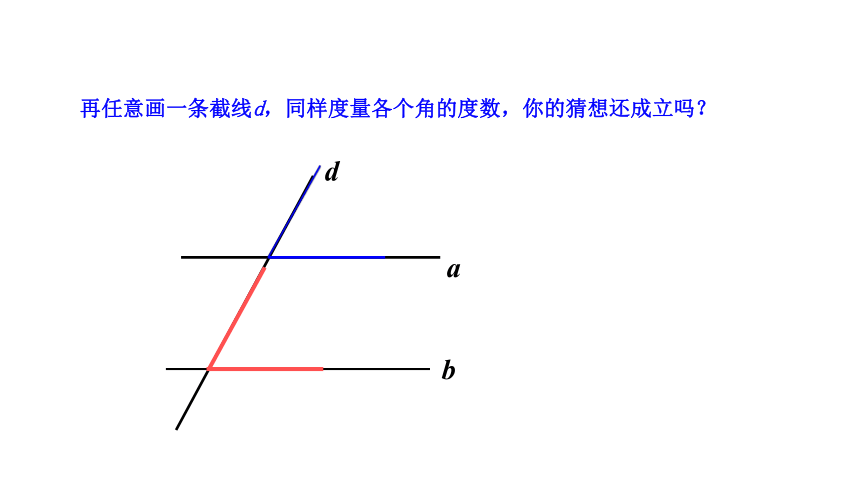
再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?
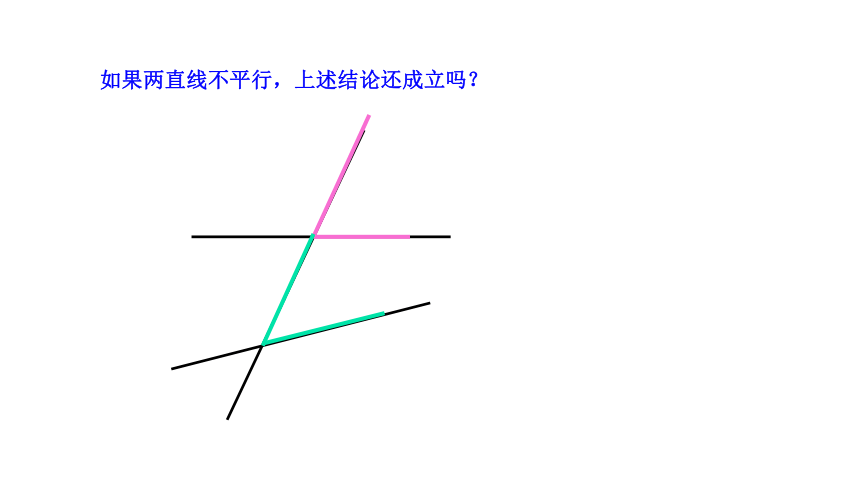
如果两直线不平行,上述结论还成立吗?
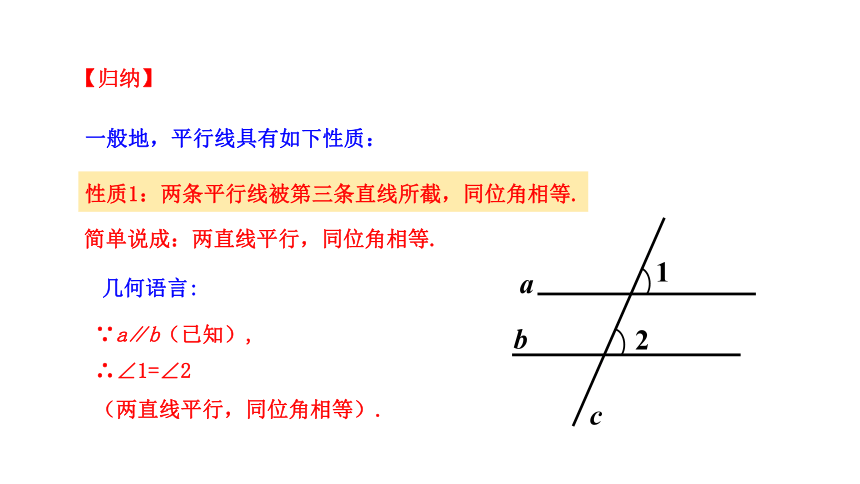
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等).
∵a∥b(已知),
几何语言:
简单说成:两直线平行,同位角相等.
【归纳】
例1 如图,若AB∥CD,且∠1=∠2,试判断AM与CN的位置关系,
并说明理由.
【解析】
AM∥CN.
理由:∵AB∥CD(已知),
∴∠BAE=∠ACD(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠EAM=∠ECN(等式性质).
∴AM∥CN(同位角相等,两直线平行).
【例题】
如图所示,∠1=70°,若m∥n,则∠2= .
如图所示,直线m∥n,∠1=70°,∠2=30°,则∠A 等于 ( )
A. 30° B. 35°
C. 40° D. 50°
70°
C
n
m
2
1
【跟踪训练】
在上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等,能否得到内错角之间的数量关系?
两直线平行,内错角相等
如图,已知a//b,那么 2与 3相等吗?为什么
【解析】
∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
【跟踪训练】
性质2:两条平行线被第三条直线所截,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等).
∵a∥b(已知),
几何语言:
简单说成:两直线平行,内错角相等.
【归纳】
例2 如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.
a
b
c
1
2
∴∠ 2= 50° (等量代换).
∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 50° (已知),
【例题】
【解析】
如图所示,AC∥BD,∠A=70°,∠C=50°,则
∠1= ,∠2= ,∠3= .
70°
50°
60°
【跟踪训练】
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a//b (已知),
∴ 1= 2(两直线平行,同位角相等).
∵ 1+ 4=180°(邻补角的性质),
∴ 2+ 4=180°(等量代换).
类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
两直线平行,同旁内角互补
性质3:两条平行线被第三条直线所截,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补).
∵a∥b(已知),
几何语言:
简单说成:两直线平行,同旁内角互补.
【归纳】
例3 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
【解析】
解:∵梯形上、下底互相平行,
∴ ∠A与∠D 互补, ∠B 与∠C 互补.
∴梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
【例题】
如图所示,直线a∥b,直线l与a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
A. 58° B. 42°
C. 32° D. 28°
C
1
2
A
B
C
a
l
b
【跟踪训练】
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:
1.(南充·中考)如图,直线DE经过点A,DE∥BC,
∠B=60°,下列结论成立的是( )
A.∠C=60°
B.∠DAB=60°
C.∠EAC=60°
D.∠BAC=60°
【解析】因为DE∥BC, 所以∠DAB=∠B = 60°.
D
E
A
B
C
B
【解析】因为∠2=∠1(对顶角相等),
所以∠2=∠1=54°.
因为a∥b(已知),
所以∠4=∠1=54°(两直线平行,同位角相等),
∠2+∠3=180°(两直线平行,同旁内角互补),
所以∠3=180°-∠2=180°-54°=126°.
1
2
3
4
a
b
2.如图,直线a∥b,∠1=54°,∠2,∠3,∠4各是多少
度
3.如图,直线AB∥CD,DE∥BC,如果∠B=58°,
求∠D 的度数.
【解析】由直线AB∥CD,得∠B =∠BCD;由DE∥BC,得∠D=∠BCD;所以∠D=∠B=58°.
A
B
C
D
E
【解析】因为 1= 2(已知),
所以AD//BC(内错角相等,两直线平行),
所以 BCD+ D=180°
( )
两直线平行,同旁内角互补
2
1
D
C
B
A
4.如图:已知 1= 2,
试说明: BCD+ D=180°.
5.3 平行线的性质
5.3.1 平行线的性质
根据右图,填空:
①如果∠1=∠C,
那么__∥__.( )
② 如果∠1=∠B ,
那么__∥__.( )
③ 如果∠2+∠B=180°,
那么__∥__.( )
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
E
A
C
D
B
1
2
3
4
1.经历探索平行线的性质的过程.
2.掌握平行线的性质并能够灵活应用.
3.综合运用平行线的判定与性质解决问题.
画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
b
1
2
a
c
5
6
7
8
3
4
两直线平行,同位角相等
【讨论】
∠1-∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想
猜想:两条平行线被第三条直线所截,同位角___.
相等
b
1
2
a
c
5
6
7
8
3
4
a
b
d
再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?
如果两直线不平行,上述结论还成立吗?
一般地,平行线具有如下性质:
性质1:两条平行线被第三条直线所截,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等).
∵a∥b(已知),
几何语言:
简单说成:两直线平行,同位角相等.
【归纳】
例1 如图,若AB∥CD,且∠1=∠2,试判断AM与CN的位置关系,
并说明理由.
【解析】
AM∥CN.
理由:∵AB∥CD(已知),
∴∠BAE=∠ACD(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠EAM=∠ECN(等式性质).
∴AM∥CN(同位角相等,两直线平行).
【例题】
如图所示,∠1=70°,若m∥n,则∠2= .
如图所示,直线m∥n,∠1=70°,∠2=30°,则∠A 等于 ( )
A. 30° B. 35°
C. 40° D. 50°
70°
C
n
m
2
1
【跟踪训练】
在上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等,能否得到内错角之间的数量关系?
两直线平行,内错角相等
如图,已知a//b,那么 2与 3相等吗?为什么
【解析】
∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
b
1
2
a
c
3
【跟踪训练】
性质2:两条平行线被第三条直线所截,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等).
∵a∥b(已知),
几何语言:
简单说成:两直线平行,内错角相等.
【归纳】
例2 如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.
a
b
c
1
2
∴∠ 2= 50° (等量代换).
∵ a∥b(已知),
∴∠ 1= ∠ 2
(两直线平行,内错角相等).
又∵∠ 1 = 50° (已知),
【例题】
【解析】
如图所示,AC∥BD,∠A=70°,∠C=50°,则
∠1= ,∠2= ,∠3= .
70°
50°
60°
【跟踪训练】
如图,已知a//b,那么 2与 4有什么关系呢?为什么
b
1
2
a
c
4
解: ∵a//b (已知),
∴ 1= 2(两直线平行,同位角相等).
∵ 1+ 4=180°(邻补角的性质),
∴ 2+ 4=180°(等量代换).
类似地,已知两直线平行,能否得到同旁内角之间的数量关系?
两直线平行,同旁内角互补
性质3:两条平行线被第三条直线所截,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180 °
(两直线平行,同旁内角互补).
∵a∥b(已知),
几何语言:
简单说成:两直线平行,同旁内角互补.
【归纳】
例3 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?
A
B
C
D
【解析】
解:∵梯形上、下底互相平行,
∴ ∠A与∠D 互补, ∠B 与∠C 互补.
∴梯形的另外两个角分别是80°、65°.
于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°
【例题】
如图所示,直线a∥b,直线l与a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
A. 58° B. 42°
C. 32° D. 28°
C
1
2
A
B
C
a
l
b
【跟踪训练】
性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:
1.(南充·中考)如图,直线DE经过点A,DE∥BC,
∠B=60°,下列结论成立的是( )
A.∠C=60°
B.∠DAB=60°
C.∠EAC=60°
D.∠BAC=60°
【解析】因为DE∥BC, 所以∠DAB=∠B = 60°.
D
E
A
B
C
B
【解析】因为∠2=∠1(对顶角相等),
所以∠2=∠1=54°.
因为a∥b(已知),
所以∠4=∠1=54°(两直线平行,同位角相等),
∠2+∠3=180°(两直线平行,同旁内角互补),
所以∠3=180°-∠2=180°-54°=126°.
1
2
3
4
a
b
2.如图,直线a∥b,∠1=54°,∠2,∠3,∠4各是多少
度
3.如图,直线AB∥CD,DE∥BC,如果∠B=58°,
求∠D 的度数.
【解析】由直线AB∥CD,得∠B =∠BCD;由DE∥BC,得∠D=∠BCD;所以∠D=∠B=58°.
A
B
C
D
E
【解析】因为 1= 2(已知),
所以AD//BC(内错角相等,两直线平行),
所以 BCD+ D=180°
( )
两直线平行,同旁内角互补
2
1
D
C
B
A
4.如图:已知 1= 2,
试说明: BCD+ D=180°.
