2021-2022 人教版 数学 七年级下册 6.2 立方根 课件(共23张PPT)
文档属性
| 名称 | 2021-2022 人教版 数学 七年级下册 6.2 立方根 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 948.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 11:03:44 | ||
图片预览








文档简介
(共23张PPT)
6.2 立方根
1.16的平方根是______
2.-16的平方根是_____________
3.0的平方根是______
没有平方根
0
一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根.
xcm
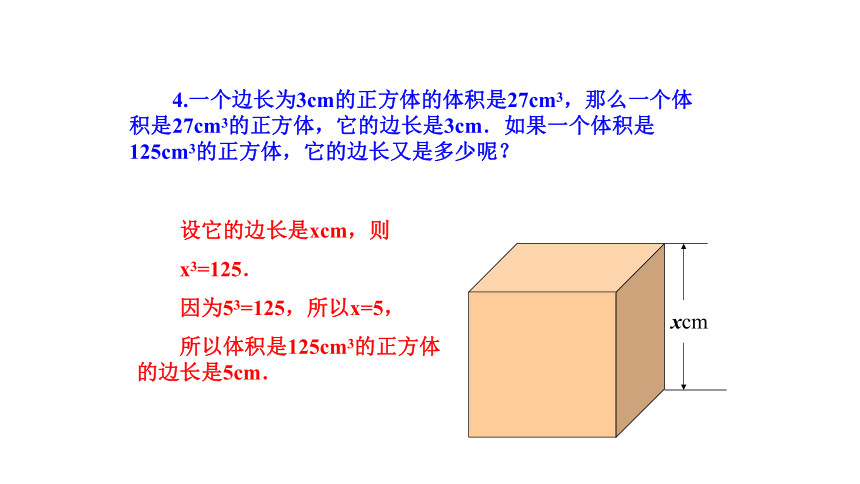
4.一个边长为3cm的正方体的体积是27cm3,那么一个体积是27cm3的正方体,它的边长是3cm.如果一个体积是125cm3的正方体,它的边长又是多少呢?
设它的边长是xcm,则
x3=125.
因为53=125,所以x=5,
所以体积是125cm3的正方体的边长是5cm.
1.了解立方根的概念,会表示一个数的立方根.
2.了解开立方与立方互为逆运算,会用立方运算求某些数的立方根.
3.体会一个数的立方根的唯一性.
4.分清一个数的立方根与平方根的区别.
思考:
(1)2的立方等于多少?是否有其他的数,
它的立方也是8
(2)-3的立方等于多少?是否有其他的数,
它的立方也是-27
什么才是一个数a的立方根呢?
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记做 (也叫做三次方根).如2是8的立方根,0是0的立方根.
表示方法:
一个数a的立方根,用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
求一个数的立方根的运算,叫做开立方.
3
= 2
开立方与立方是互逆运算
-2
求下列各数的立方根
(1)27. (2)-27. (3) (4)-0.064. (5)0.
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(3)∵
∴ 的立方根是
【解析】
【例题】
(4)
∴-0.064的立方根是-0.4
∵0 =0
3
∴0的立方根是0
∵
(5)
正数、0、负数的立方根各有
什么特点?
与被开方数符号相同
【思考】
(1)1的平方根是____;立方根为____;
算术平方根为_____.
(2)平方根是它本身的数是____.
(3)立方根是其本身的数是____.
(4)算术平方根是其本身的数是____.
(5) 的平方根为 .
(6) 的立方根为_____.
填空
【跟踪训练】
正数有立方根吗?如果有,有几个
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根;
零的立方根是零.
【归纳】
被开方数 平方根 立方根
正数
负数
零
你能归纳出平方根和立方根的异同点吗
有两个,互为相反数
无平方根
零
有一个,是正数
有一个,是负数
零
【归纳】
1.因为33=27,所以 =___.
2.因为(-4)3=-64,所以 =____.
3.因为x3=a,所以 =____.
3
-4
x
求一个数的立方根的运算叫做开立方,a叫做被开方数.
求立方根(开立方)
求下列各式的值:
(1) ; (2) ;
(3) ; (4) .
解:
(1)因为103=1 000,所以 =10;
(2)因为(-0.1)3=-0.001,所以 =-0.1;
(3)因为(-1)3=-1,所以 =-1;
(4)因为 所以
【例题】
求下列各式的值:
【解析】
【跟踪训练】
与 的性质
想一想
表示a的立方根,那么 等于什么?
呢?
1.任何一个数既等于这个数的立方根的立方
又等于这个数的立方的立方根.
即:
2.负号可直接从立方根内移到立方根外.
即:
立方根
定义 一般地,如果一个数的立方等于a,那么这
个数叫做a的立方根
性质 ①正数有一个立方根,仍为正数;
②负数有一个立方根,仍为负数;
③0的立方根是0
表示法 (a为任意数)
求一个负数的立方根的方法:
先求出这个负数的绝对值的立方根,然后再取它的相反
数即可;其实质是利用互为相反数的两个数的立方互为相反数.
即 来求解;也就是说三次根号内的负号可以移到三
次根号外面.
1.了解立方根的定义、性质及表示方法.
3.分清立方根和平方根的区别.
2.会求一个数的立方根.
1.(烟台·中考)-8的立方根是( )
A. 2 B. -2 C. D.
【解析】因为 ,所以 .
B
2.要使 ,k的取值为( )
A.k≤3 B.k≥3
C.0≤k≤ 3 D.一切实数
D
C
4.下列说法正确的是( )
A. 负数没有立方根
B. -9的立方根是
C. =3
D. 任何正数都有两个立方根,它们互为相反数
B
分析:
任何一个数都有唯一的立方根,所以选项A,D不
正确,因为33=27,所以 ,故选项C也不正确,选项B正确.
5.一个数的平方等于64,则这个数的立方根是_____.
【解析】64的平方根为±8,8的立方根为2,-8的立方根
为-2.故为2或-2.
2或-2
6.2 立方根
1.16的平方根是______
2.-16的平方根是_____________
3.0的平方根是______
没有平方根
0
一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根.
xcm
4.一个边长为3cm的正方体的体积是27cm3,那么一个体积是27cm3的正方体,它的边长是3cm.如果一个体积是125cm3的正方体,它的边长又是多少呢?
设它的边长是xcm,则
x3=125.
因为53=125,所以x=5,
所以体积是125cm3的正方体的边长是5cm.
1.了解立方根的概念,会表示一个数的立方根.
2.了解开立方与立方互为逆运算,会用立方运算求某些数的立方根.
3.体会一个数的立方根的唯一性.
4.分清一个数的立方根与平方根的区别.
思考:
(1)2的立方等于多少?是否有其他的数,
它的立方也是8
(2)-3的立方等于多少?是否有其他的数,
它的立方也是-27
什么才是一个数a的立方根呢?
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.记做 (也叫做三次方根).如2是8的立方根,0是0的立方根.
表示方法:
一个数a的立方根,用符号“ ”表示,读作“三次根号a”,其中a是被开方数,3是根指数.
其中a是被开方数,3是根指数,符号“ ”读做“三次根号”.
3
求一个数的立方根的运算,叫做开立方.
3
= 2
开立方与立方是互逆运算
-2
求下列各数的立方根
(1)27. (2)-27. (3) (4)-0.064. (5)0.
(1)∵
∴27的立方根是3
即
(2)∵
∴-27的立方根是-3
即
(3)∵
∴ 的立方根是
【解析】
【例题】
(4)
∴-0.064的立方根是-0.4
∵0 =0
3
∴0的立方根是0
∵
(5)
正数、0、负数的立方根各有
什么特点?
与被开方数符号相同
【思考】
(1)1的平方根是____;立方根为____;
算术平方根为_____.
(2)平方根是它本身的数是____.
(3)立方根是其本身的数是____.
(4)算术平方根是其本身的数是____.
(5) 的平方根为 .
(6) 的立方根为_____.
填空
【跟踪训练】
正数有立方根吗?如果有,有几个
负数呢?
零呢?
一个正数有一个正的立方根;
一个负数有一个负的立方根;
零的立方根是零.
【归纳】
被开方数 平方根 立方根
正数
负数
零
你能归纳出平方根和立方根的异同点吗
有两个,互为相反数
无平方根
零
有一个,是正数
有一个,是负数
零
【归纳】
1.因为33=27,所以 =___.
2.因为(-4)3=-64,所以 =____.
3.因为x3=a,所以 =____.
3
-4
x
求一个数的立方根的运算叫做开立方,a叫做被开方数.
求立方根(开立方)
求下列各式的值:
(1) ; (2) ;
(3) ; (4) .
解:
(1)因为103=1 000,所以 =10;
(2)因为(-0.1)3=-0.001,所以 =-0.1;
(3)因为(-1)3=-1,所以 =-1;
(4)因为 所以
【例题】
求下列各式的值:
【解析】
【跟踪训练】
与 的性质
想一想
表示a的立方根,那么 等于什么?
呢?
1.任何一个数既等于这个数的立方根的立方
又等于这个数的立方的立方根.
即:
2.负号可直接从立方根内移到立方根外.
即:
立方根
定义 一般地,如果一个数的立方等于a,那么这
个数叫做a的立方根
性质 ①正数有一个立方根,仍为正数;
②负数有一个立方根,仍为负数;
③0的立方根是0
表示法 (a为任意数)
求一个负数的立方根的方法:
先求出这个负数的绝对值的立方根,然后再取它的相反
数即可;其实质是利用互为相反数的两个数的立方互为相反数.
即 来求解;也就是说三次根号内的负号可以移到三
次根号外面.
1.了解立方根的定义、性质及表示方法.
3.分清立方根和平方根的区别.
2.会求一个数的立方根.
1.(烟台·中考)-8的立方根是( )
A. 2 B. -2 C. D.
【解析】因为 ,所以 .
B
2.要使 ,k的取值为( )
A.k≤3 B.k≥3
C.0≤k≤ 3 D.一切实数
D
C
4.下列说法正确的是( )
A. 负数没有立方根
B. -9的立方根是
C. =3
D. 任何正数都有两个立方根,它们互为相反数
B
分析:
任何一个数都有唯一的立方根,所以选项A,D不
正确,因为33=27,所以 ,故选项C也不正确,选项B正确.
5.一个数的平方等于64,则这个数的立方根是_____.
【解析】64的平方根为±8,8的立方根为2,-8的立方根
为-2.故为2或-2.
2或-2
