第18章 平行四边形单元测试题(含答案)
文档属性
| 名称 | 第18章 平行四边形单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 563.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-18 17:30:48 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.在平行四边形ABCD中,AB=7,BC=10,则平行四边形ABCD的周长为( )
A.17 B.34 C.24 D.40
2.下列命题中,能判断四边形是矩形的是( )
A.对角线相等 B.对角线互相平分
C.对角线相等且互相平分 D.对角线互相垂直
3.如图,在平行四边形ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
A.2cm B.4cm C.6cm D.8cm
4.在平行四边形ABCD中,对角线AC、BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a-1,b+2),C(3,1),则点D的坐标是( )
A.(4,-1) B.(-3,-1) C.(2,3) D.(-4,1)
5.如图,在菱形ABCD中,AC与BD相交于点O,AC=6,BD=8,则菱形边长AB等于( )
A.10 B. C.5 D.6
5题图 6题图 7题图
6.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
7.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=4,则该矩形的面积是( )
A.16 B.8 C.16 D.8
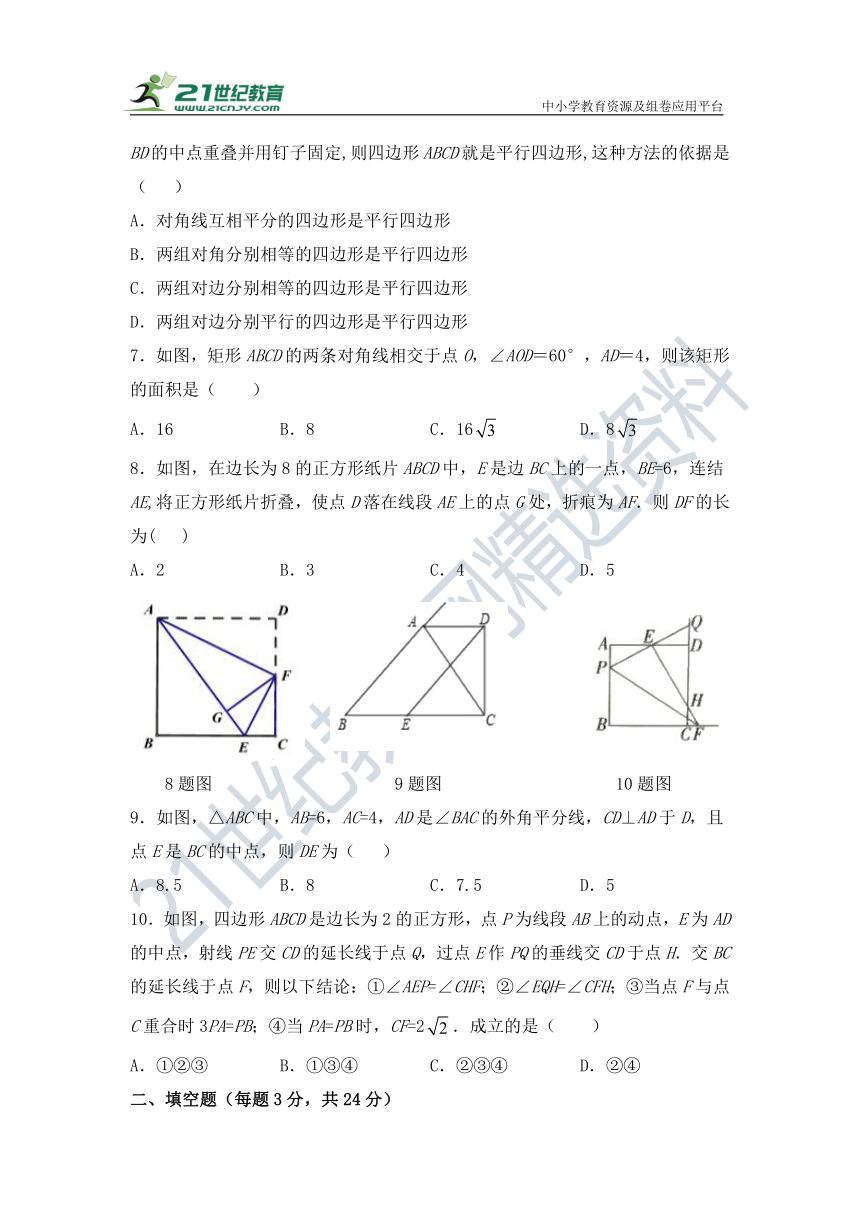
8.如图,在边长为8的正方形纸片ABCD中,E是边BC上的一点,BE=6,连结AE,将正方形纸片折叠,使点D落在线段AE上的点G处,折痕为AF.则DF的长为( )
A.2 B.3 C.4 D.5
8题图 9题图 10题图
9.如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE为( )
A.8.5 B.8 C.7.5 D.5
10.如图,四边形ABCD是边长为2的正方形,点P为线段AB上的动点,E为AD的中点,射线PE交CD的延长线于点Q,过点E作PQ的垂线交CD于点H.交BC的延长线于点F,则以下结论:①∠AEP=∠CHF;②∠EQH=∠CFH;③当点F与点C重合时3PA=PB;④当PA=PB时,CF=2.成立的是( )
A.①②③ B.①③④ C.②③④ D.②④
二、填空题(每题3分,共24分)
11.如果顺次联结四边形ABCD各边中点所得的四边形是矩形,那么对角线AC与BD需满足的条件是__.
12.如图,在菱形ABCD中,对角线AC=4,BD=2,AC,BD相交于点O,过点C作CE⊥AB交AB的延长线于点E,过点O作OF⊥CE交CE于点F,则OF的长度为__.
13.如图,直角坐标系中,原点O是的对称中心,点A在x正半轴上,点B在第一象限,边交y轴于点E,,则点D的坐标为________.
14.如图,在周长为16,面积为6的矩形纸片中,是的中点.是上一动点,将沿直线折叠,点落在点处.在上任取一点,连接,,则的最小值为___________.
15.如图,在边长为4的正方形ABCD中,点E,F分别是边AB、BC的中点,连接EC、DF,点G、H分别是EC、DF的中点,连接GH,则GH的长度为___.
16.如图,菱形ABCD与矩形BNDM有公共的对角线BD,M,N在AC上,且AC=2BD,则DA:MD=________.
17. 如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小 .
18BO的中点。若AC+BD=24cm,△OAB的周长是20cm,则EF= cm。
三、解答题(本题共有6小题,共46分,19题6分,20—24题8分)
19.(6分)如图,平行四边形的对角线交于点,若,,,求的长
20.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
21.如图,在平行四边形中,对角线与相交于点,点在对角线上,且,求证:
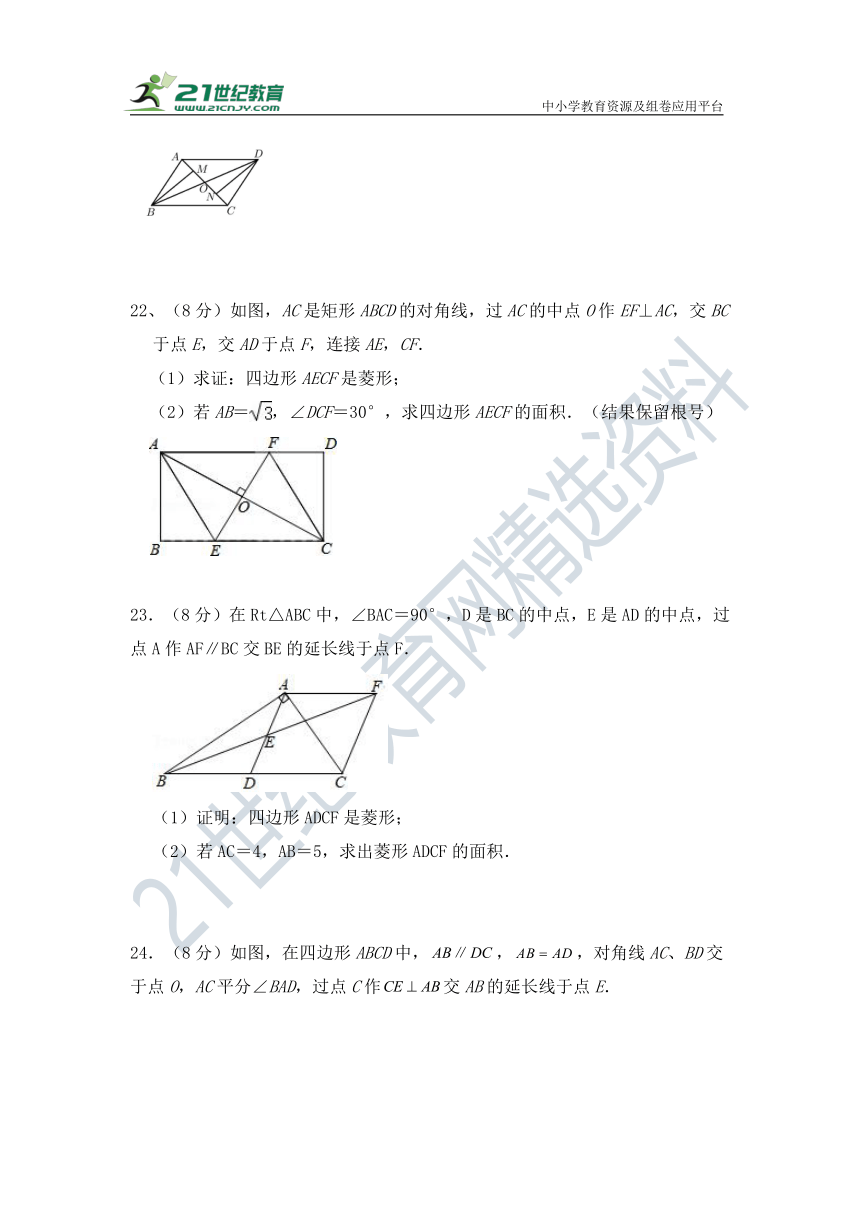
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.(8分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明:四边形ADCF是菱形;
(2)若AC=4,AB=5,求出菱形ADCF的面积.
24.(8分)如图,在四边形ABCD中,,,对角线AC、BD交于点O,AC平分∠BAD,过点C作交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,,求CE的长.
参考答案
1.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A D A D D B B B
二.填空题
11.AC⊥BD
12.
13.
14.
15.2
16.
17. 120°
18. 4
三、解答题
19.解:∵四边形ABCD是平行四边形,,,
∴,,AB=CD;
∵,
∴,
∴∠BCA=90°,
∴,
∴.
20.证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
21.解:∵四边形是平行四边形
∴,
又∵
∴
∴
在和中
∴
∴
∴
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23. (1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
∴AF=DB,
∵AD为BC边上的中线,
∴DB=DC,
∴AF=CD,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴ ,
∴平行四边形ADCF是菱形
(2)解:∵D是BC的中点,
∴S菱形ADCF=2S△ADC=S△ABC= AB AC= ×5×4=10
24.(1)证明:∵,
∴,
∵AC平分∠BAD,
∴,
∴,
∴,
∵AB=AD,
∴,
∵,
∴四边形ABCD是平行四边形,
又∵,
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,BD=6,AC=8,
∴,,,
∴,
在中,根据勾股定理可知,
,
∴菱形的面积,
∵,
∴菱形面积,
∴
第18章 《平行四边形》单元测试
题号 一 二 三 总分
19 20 21 22 23 24
分数
一.选择题(每题3分,共30分)
1.在平行四边形ABCD中,AB=7,BC=10,则平行四边形ABCD的周长为( )
A.17 B.34 C.24 D.40
2.下列命题中,能判断四边形是矩形的是( )
A.对角线相等 B.对角线互相平分
C.对角线相等且互相平分 D.对角线互相垂直
3.如图,在平行四边形ABCD中,已知AD=8cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE等于( )
A.2cm B.4cm C.6cm D.8cm
4.在平行四边形ABCD中,对角线AC、BD相交于点O,以点O为坐标原点建立平面直角坐标系,其中A(a,b),B(a-1,b+2),C(3,1),则点D的坐标是( )
A.(4,-1) B.(-3,-1) C.(2,3) D.(-4,1)
5.如图,在菱形ABCD中,AC与BD相交于点O,AC=6,BD=8,则菱形边长AB等于( )
A.10 B. C.5 D.6
5题图 6题图 7题图
6.小玲的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC、BD的中点重叠并用钉子固定,则四边形ABCD就是平行四边形,这种方法的依据是( )
A.对角线互相平分的四边形是平行四边形
B.两组对角分别相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形
D.两组对边分别平行的四边形是平行四边形
7.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=4,则该矩形的面积是( )
A.16 B.8 C.16 D.8
8.如图,在边长为8的正方形纸片ABCD中,E是边BC上的一点,BE=6,连结AE,将正方形纸片折叠,使点D落在线段AE上的点G处,折痕为AF.则DF的长为( )
A.2 B.3 C.4 D.5
8题图 9题图 10题图
9.如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE为( )
A.8.5 B.8 C.7.5 D.5
10.如图,四边形ABCD是边长为2的正方形,点P为线段AB上的动点,E为AD的中点,射线PE交CD的延长线于点Q,过点E作PQ的垂线交CD于点H.交BC的延长线于点F,则以下结论:①∠AEP=∠CHF;②∠EQH=∠CFH;③当点F与点C重合时3PA=PB;④当PA=PB时,CF=2.成立的是( )
A.①②③ B.①③④ C.②③④ D.②④
二、填空题(每题3分,共24分)
11.如果顺次联结四边形ABCD各边中点所得的四边形是矩形,那么对角线AC与BD需满足的条件是__.
12.如图,在菱形ABCD中,对角线AC=4,BD=2,AC,BD相交于点O,过点C作CE⊥AB交AB的延长线于点E,过点O作OF⊥CE交CE于点F,则OF的长度为__.
13.如图,直角坐标系中,原点O是的对称中心,点A在x正半轴上,点B在第一象限,边交y轴于点E,,则点D的坐标为________.
14.如图,在周长为16,面积为6的矩形纸片中,是的中点.是上一动点,将沿直线折叠,点落在点处.在上任取一点,连接,,则的最小值为___________.
15.如图,在边长为4的正方形ABCD中,点E,F分别是边AB、BC的中点,连接EC、DF,点G、H分别是EC、DF的中点,连接GH,则GH的长度为___.
16.如图,菱形ABCD与矩形BNDM有公共的对角线BD,M,N在AC上,且AC=2BD,则DA:MD=________.
17. 如图,在平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=150°,则∠A的大小 .
18BO的中点。若AC+BD=24cm,△OAB的周长是20cm,则EF= cm。
三、解答题(本题共有6小题,共46分,19题6分,20—24题8分)
19.(6分)如图,平行四边形的对角线交于点,若,,,求的长
20.如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
21.如图,在平行四边形中,对角线与相交于点,点在对角线上,且,求证:
22、(8分)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
23.(8分)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明:四边形ADCF是菱形;
(2)若AC=4,AB=5,求出菱形ADCF的面积.
24.(8分)如图,在四边形ABCD中,,,对角线AC、BD交于点O,AC平分∠BAD,过点C作交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,,求CE的长.
参考答案
1.选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A D A D D B B B
二.填空题
11.AC⊥BD
12.
13.
14.
15.2
16.
17. 120°
18. 4
三、解答题
19.解:∵四边形ABCD是平行四边形,,,
∴,,AB=CD;
∵,
∴,
∴∠BCA=90°,
∴,
∴.
20.证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=AD,
在△ABE和△ADF中,
,
∴△ABE≌△ADF(ASA),
∴AE=AF.
21.解:∵四边形是平行四边形
∴,
又∵
∴
∴
在和中
∴
∴
∴
22、(1)证明:∵O是AC的中点,且EF⊥AC,
∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠AFO=∠CEO,
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴AF=CE,
∴AF=CF=CE=AE,
∴四边形AECF是菱形;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=,
在Rt△CDF中,cos∠DCF=,∠DCF=30°,
∴CF==2,
∵四边形AECF是菱形,
∴CE=CF=2,
∴四边形AECF是的面积为:EC AB=2.
23. (1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEB中,
,
∴△AEF≌△DEB(AAS);
∴AF=DB,
∵AD为BC边上的中线,
∴DB=DC,
∴AF=CD,
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴ ,
∴平行四边形ADCF是菱形
(2)解:∵D是BC的中点,
∴S菱形ADCF=2S△ADC=S△ABC= AB AC= ×5×4=10
24.(1)证明:∵,
∴,
∵AC平分∠BAD,
∴,
∴,
∴,
∵AB=AD,
∴,
∵,
∴四边形ABCD是平行四边形,
又∵,
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,BD=6,AC=8,
∴,,,
∴,
在中,根据勾股定理可知,
,
∴菱形的面积,
∵,
∴菱形面积,
∴
