平行线及其判定
图片预览




文档简介
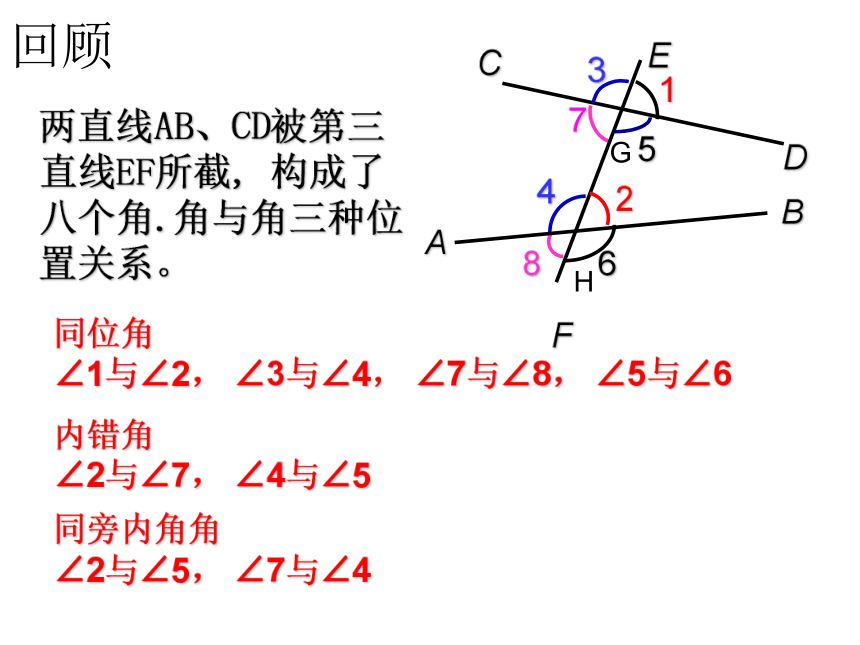
课件23张PPT。回顾两直线AB、CD被第三直线EF所截, 构成了八个角.角与角三种位置关系。同位角
∠1与∠2, ∠3与∠4, ∠7与∠8, ∠5与∠6 内错角
∠2与∠7, ∠4与∠5同旁内角角
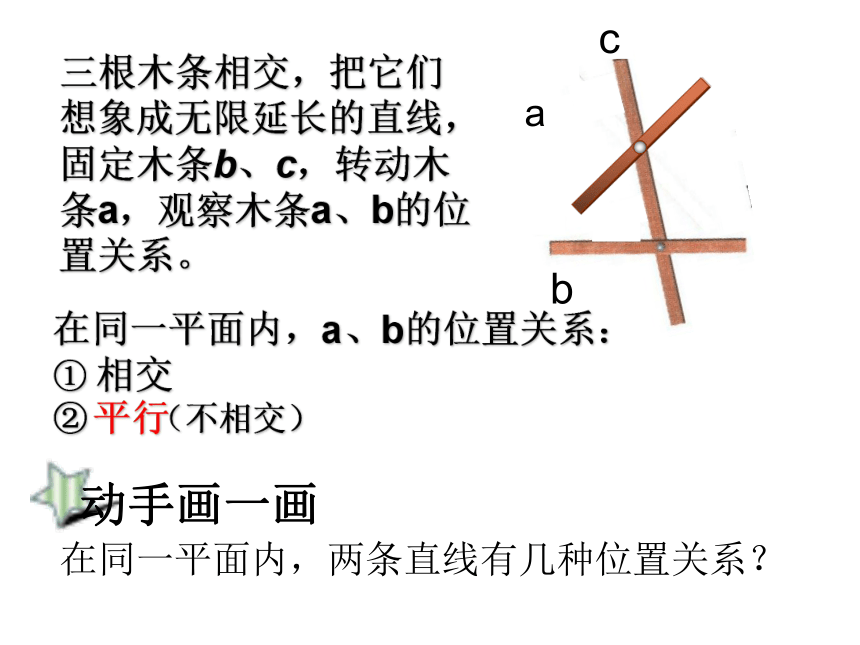
∠2与∠5, ∠7与∠45.2平行线前面我们一直学的两条直线怎样位置关系?两条直线相交三根木条相交,把它们想象成无限延长的直线,固定木条b、c,转动木条a,观察木条a、b的位置关系。在同一平面内,a、b的位置关系:
① 相交
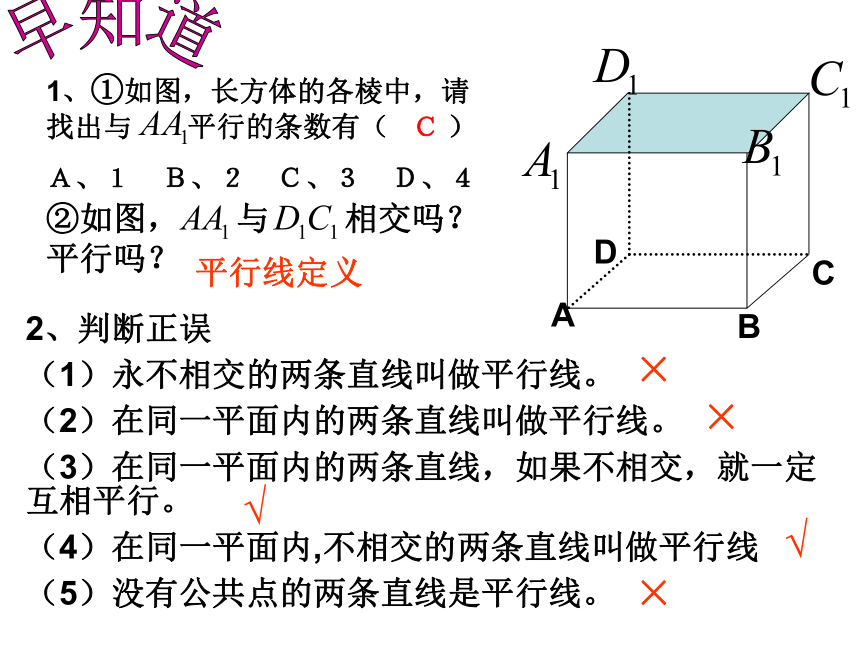
② (不相交)平行在同一平面内,两条直线有几种位置关系?动手画一画一.平行线的定义:在同一平面内,不相交的两条直线叫做平行线。1、在同 一平面内平行线有什么特征?2、不相交返回数学来源于生活1、①如图,长方体的各棱中,请找出与 平行的条数有( )
A、1 B、2 C、3 D、4C2、判断正误
(1)永不相交的两条直线叫做平行线。
(2)在同一平面内的两条直线叫做平行线。
(3)在同一平面内的两条直线,如果不相交,就一定互相平行。
(4)在同一平面内,不相交的两条直线叫做平行线
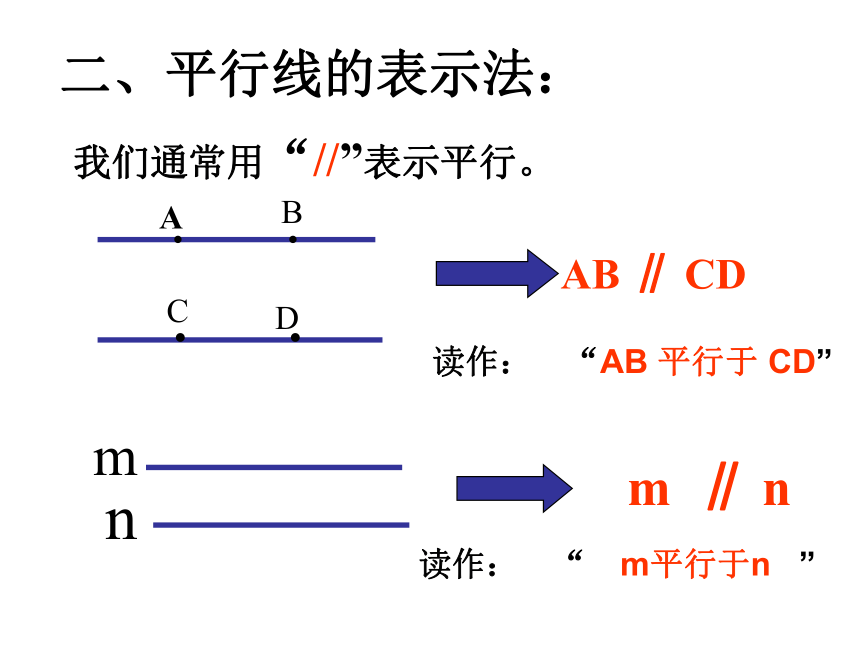
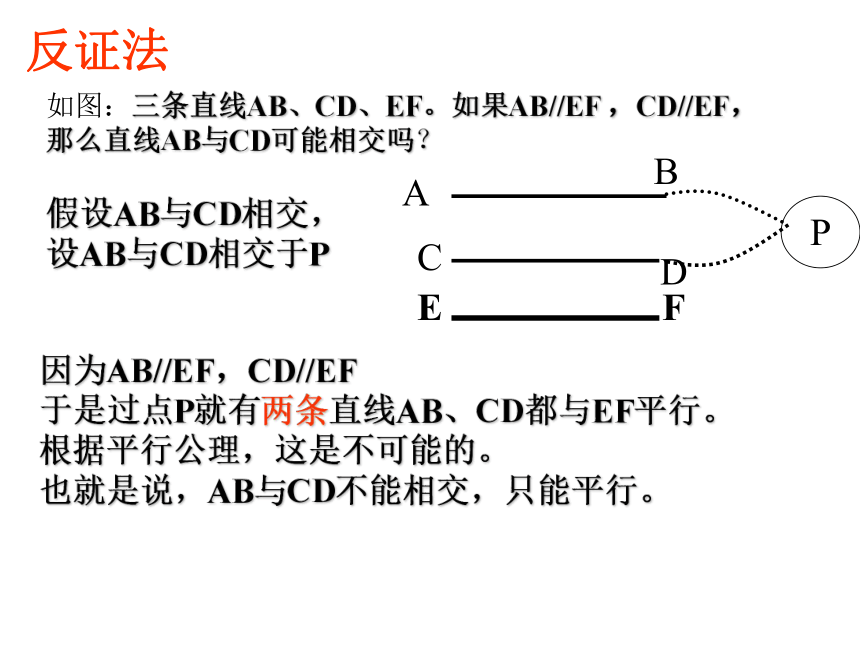
(5)没有公共点的两条直线是平行线。早知道②如图, 与 相交吗?平行吗?平行线定义××√√×我们通常用“//”表示平行。二、平行线的表示法:读作: “AB 平行于 CD” 读作: “ m平行于n ” (3)经过点C能画出几条直线与直线AB平行? (4)过点D画一条直线与直线AB平行,它与(3)中所画的直线平行吗?①经过直线外一点,有且只有一条直线与已知直线平行。②如果两条直线都与第三条直线平行,那么这两条直线互相平行。··CD平行公理动动手数学语言:如果a//AB,b//AB,那么a//b. (1)经过点C能画出几条直线?无数条1条ab (2)与直线AB平行的直线有几条?无数条推论基本事实如图:三条直线AB、CD、EF。如果AB//EF ,CD//EF,
那么直线AB与CD可能相交吗?FEDCBA假设AB与CD相交,
设AB与CD相交于P因为AB//EF,CD//EF
于是过点P就有两条直线AB、CD都与EF平行。
根据平行公理,这是不可能的。
也就是说,AB与CD不能相交,只能平行。反证法1、下列语句中,正确的个数是 ( )
(1)不相交的两条直线是平行线
(2)同一平面内,两直线的位置关系有两种,即相交或平行
(3)若线段AB与CD没有交点则AB//CD
(4)若a//b,b//c,则a 与c不相交
(A)1个 (B)2个 (C)3个 (D)4个2、已知直线L1与L2都经过点P,并且L1//L3,L2//L3,那么L1与L2必须重合,这是因为 。3、下列说法正确的是( )
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行试一试4、如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?解: ∵ a ∥b,b∥c,
∴ a ∥c
( )如果两条直线都与第三条直线平行,那么这两条直线互相平行如果两条直线都与第三条直线平行,那么这两条直线互相平行 ∵ c∥d,
∴ a ∥d
( )2、下列推理正确的是( )A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。C平行线的画法1、过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?· A B P 5.2.2平行线的判定一、贴二、靠三、推四、画2、在这一过程中三角尺起着什么样的作用?· A B P21问题2:由两直线平行判定1,能否
利用内错角或同旁内角来证明两直
线平行?如:
(1)内错角:∠1与∠3
内错角相等,两直线平行。
(2)同旁内角:∠1与∠4
同旁内角互补,两直线平行。∠1与∠2是同位角,
且∠1=∠2两直线平行判定1:思考:什么情况下两直线平行?同位角相等,两直线平行。问题1:∠1与∠2是什么位置关系?它们的大小有什么关系?1.如图,如果 ∠2=∠3,能得出CD∥EF吗?DACB2FE转化为方法一同位角相等,两直线平行。2.如图,若∠2+∠4=180°能得出CD∥EF吗?∠1=∠3∠3+∠4=180°∠2=∠3 已知∠2=∠3∠2=∠1思路 :∠2+∠4=180°∠1+∠4=180°思路:转化为方法一转化为方法二 内错角相等,两直线平行。数形结合思路转化∠2=∠1143通过“对顶角相等、邻补角互补”实现了新知向旧知的转化。思想:例:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?12解:
∵a⊥b,c⊥a
∴∠1=∠2=90°
∴b∥c
( )分析:两条直线平行的方法。同位角相等,两直线平行。结论:
垂直于同一条直线的两条直线平行.1、如图:点E在AC的延长线
上,下列条件中能判断
AB∥CD的是( )课堂检测CDA4B321EA、∠3=∠4 B、∠1=∠2
C、∠D=∠DCE D、∠D+∠ACD=180°B找内错角就是找字母“Z”,平行线在“Z”的两条横线上。识图小窍门OCBAED31°C屋架横梁课后题DA120°60°B 弯形管道2、图中管道AB∥CD吗?为什么?生活中的数学1、如图,为加固房屋需 添一根横梁DE,使DE∥BC,如果∠ABC=31°,那么∠ADE应为多少度?为什么?同旁内角互补,两直线平行同位角相等,两直线平行你是数学小天才!31°找同旁内角就是找字母“U”,平行线在“U”的两条竖线上识图小窍门BCDA1∠1=∠B2、如图若∠1=55°,∠B=55°,∠C=125°图中的
平行线有_____________∠C+∠B=180°BCDA1找同位角就是找字母“F”,平行线在“F”的两条横线上生活中的数学你是数学小天才!3、如图,一辆汽车两次拐弯后,行驶方向与原方向
平行,那么这两次拐弯的角度是( )
A、第一次向右拐60°,第二次向左拐120°
B、第一次向右拐120°,第二次向左拐120°
C、第一次向右拐120°,第二次向左拐60°
D、第一次向右拐60°,第二次向右拐60°CBBABCDA4、如图∵∠2=∠4,(已知)
∴___∥____( )
∵∠3=∠5,(已知)
∴___∥____( )
∵∠C+ ∠4+∠5=180°(已知)
∴______+_____=180°
∴____∥_____( )5432ABCD内错角相等,两直线平行。ADBC内错角相等,两直线平行。∠ADC∠ C课堂检测ADBC同旁内角互补,两直线平行。 本节课你的收获是什么?(1) 平行线的定义; (2)平行线的表示方法;(3)两条直线在同一平面内的位置关系。(4)平行线的画法。(5)平行线公理:经过直线外一点,有且只有一条直线与这条直线平行.(6)平行线公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.小结小结1、利用角来判定两直线平行:方法一:同位角相等,两直线平行。方法二:内错角相等,两直线平行。方法三:同旁内角互补,两直线平行。2、这节课中我们是怎样利用“同位角相等两直线平行”得到方法二和方法三的? 注意体会新知向已知转化的数学思想。 方法四:如果两条直线都与第三条直线平行,那么这两条直线互相平行
∠1与∠2, ∠3与∠4, ∠7与∠8, ∠5与∠6 内错角
∠2与∠7, ∠4与∠5同旁内角角
∠2与∠5, ∠7与∠45.2平行线前面我们一直学的两条直线怎样位置关系?两条直线相交三根木条相交,把它们想象成无限延长的直线,固定木条b、c,转动木条a,观察木条a、b的位置关系。在同一平面内,a、b的位置关系:
① 相交
② (不相交)平行在同一平面内,两条直线有几种位置关系?动手画一画一.平行线的定义:在同一平面内,不相交的两条直线叫做平行线。1、在同 一平面内平行线有什么特征?2、不相交返回数学来源于生活1、①如图,长方体的各棱中,请找出与 平行的条数有( )
A、1 B、2 C、3 D、4C2、判断正误
(1)永不相交的两条直线叫做平行线。
(2)在同一平面内的两条直线叫做平行线。
(3)在同一平面内的两条直线,如果不相交,就一定互相平行。
(4)在同一平面内,不相交的两条直线叫做平行线
(5)没有公共点的两条直线是平行线。早知道②如图, 与 相交吗?平行吗?平行线定义××√√×我们通常用“//”表示平行。二、平行线的表示法:读作: “AB 平行于 CD” 读作: “ m平行于n ” (3)经过点C能画出几条直线与直线AB平行? (4)过点D画一条直线与直线AB平行,它与(3)中所画的直线平行吗?①经过直线外一点,有且只有一条直线与已知直线平行。②如果两条直线都与第三条直线平行,那么这两条直线互相平行。··CD平行公理动动手数学语言:如果a//AB,b//AB,那么a//b. (1)经过点C能画出几条直线?无数条1条ab (2)与直线AB平行的直线有几条?无数条推论基本事实如图:三条直线AB、CD、EF。如果AB//EF ,CD//EF,
那么直线AB与CD可能相交吗?FEDCBA假设AB与CD相交,
设AB与CD相交于P因为AB//EF,CD//EF
于是过点P就有两条直线AB、CD都与EF平行。
根据平行公理,这是不可能的。
也就是说,AB与CD不能相交,只能平行。反证法1、下列语句中,正确的个数是 ( )
(1)不相交的两条直线是平行线
(2)同一平面内,两直线的位置关系有两种,即相交或平行
(3)若线段AB与CD没有交点则AB//CD
(4)若a//b,b//c,则a 与c不相交
(A)1个 (B)2个 (C)3个 (D)4个2、已知直线L1与L2都经过点P,并且L1//L3,L2//L3,那么L1与L2必须重合,这是因为 。3、下列说法正确的是( )
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行试一试4、如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?解: ∵ a ∥b,b∥c,
∴ a ∥c
( )如果两条直线都与第三条直线平行,那么这两条直线互相平行如果两条直线都与第三条直线平行,那么这两条直线互相平行 ∵ c∥d,
∴ a ∥d
( )2、下列推理正确的是( )A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。C平行线的画法1、过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?· A B P 5.2.2平行线的判定一、贴二、靠三、推四、画2、在这一过程中三角尺起着什么样的作用?· A B P21问题2:由两直线平行判定1,能否
利用内错角或同旁内角来证明两直
线平行?如:
(1)内错角:∠1与∠3
内错角相等,两直线平行。
(2)同旁内角:∠1与∠4
同旁内角互补,两直线平行。∠1与∠2是同位角,
且∠1=∠2两直线平行判定1:思考:什么情况下两直线平行?同位角相等,两直线平行。问题1:∠1与∠2是什么位置关系?它们的大小有什么关系?1.如图,如果 ∠2=∠3,能得出CD∥EF吗?DACB2FE转化为方法一同位角相等,两直线平行。2.如图,若∠2+∠4=180°能得出CD∥EF吗?∠1=∠3∠3+∠4=180°∠2=∠3 已知∠2=∠3∠2=∠1思路 :∠2+∠4=180°∠1+∠4=180°思路:转化为方法一转化为方法二 内错角相等,两直线平行。数形结合思路转化∠2=∠1143通过“对顶角相等、邻补角互补”实现了新知向旧知的转化。思想:例:在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?12解:
∵a⊥b,c⊥a
∴∠1=∠2=90°
∴b∥c
( )分析:两条直线平行的方法。同位角相等,两直线平行。结论:
垂直于同一条直线的两条直线平行.1、如图:点E在AC的延长线
上,下列条件中能判断
AB∥CD的是( )课堂检测CDA4B321EA、∠3=∠4 B、∠1=∠2
C、∠D=∠DCE D、∠D+∠ACD=180°B找内错角就是找字母“Z”,平行线在“Z”的两条横线上。识图小窍门OCBAED31°C屋架横梁课后题DA120°60°B 弯形管道2、图中管道AB∥CD吗?为什么?生活中的数学1、如图,为加固房屋需 添一根横梁DE,使DE∥BC,如果∠ABC=31°,那么∠ADE应为多少度?为什么?同旁内角互补,两直线平行同位角相等,两直线平行你是数学小天才!31°找同旁内角就是找字母“U”,平行线在“U”的两条竖线上识图小窍门BCDA1∠1=∠B2、如图若∠1=55°,∠B=55°,∠C=125°图中的
平行线有_____________∠C+∠B=180°BCDA1找同位角就是找字母“F”,平行线在“F”的两条横线上生活中的数学你是数学小天才!3、如图,一辆汽车两次拐弯后,行驶方向与原方向
平行,那么这两次拐弯的角度是( )
A、第一次向右拐60°,第二次向左拐120°
B、第一次向右拐120°,第二次向左拐120°
C、第一次向右拐120°,第二次向左拐60°
D、第一次向右拐60°,第二次向右拐60°CBBABCDA4、如图∵∠2=∠4,(已知)
∴___∥____( )
∵∠3=∠5,(已知)
∴___∥____( )
∵∠C+ ∠4+∠5=180°(已知)
∴______+_____=180°
∴____∥_____( )5432ABCD内错角相等,两直线平行。ADBC内错角相等,两直线平行。∠ADC∠ C课堂检测ADBC同旁内角互补,两直线平行。 本节课你的收获是什么?(1) 平行线的定义; (2)平行线的表示方法;(3)两条直线在同一平面内的位置关系。(4)平行线的画法。(5)平行线公理:经过直线外一点,有且只有一条直线与这条直线平行.(6)平行线公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行.小结小结1、利用角来判定两直线平行:方法一:同位角相等,两直线平行。方法二:内错角相等,两直线平行。方法三:同旁内角互补,两直线平行。2、这节课中我们是怎样利用“同位角相等两直线平行”得到方法二和方法三的? 注意体会新知向已知转化的数学思想。 方法四:如果两条直线都与第三条直线平行,那么这两条直线互相平行
