勾股定理
图片预览



文档简介
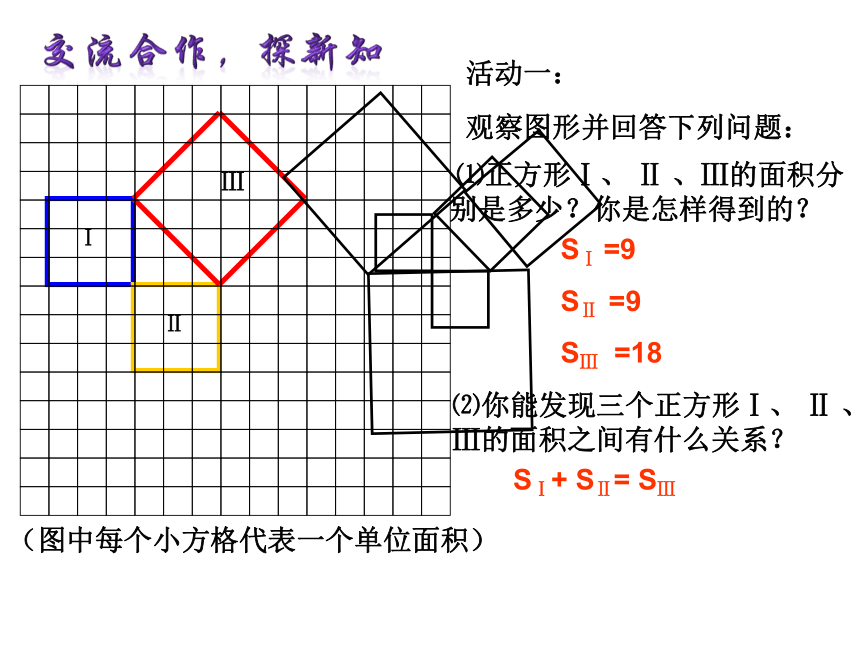
课件22张PPT。观察图形并回答下列问题:(图中每个小方格代表一个单位面积)⑵你能发现三个正方形Ⅰ、 Ⅱ 、Ⅲ的面积之间有什么关系?SⅠ+ SⅡ= SⅢ ⑴正方形Ⅰ、 Ⅱ 、Ⅲ的面积分别是多少?你是怎样得到的?SⅠ =9
SⅡ =9
SⅢ =18活动一:SⅠ + SⅡ = SⅢ
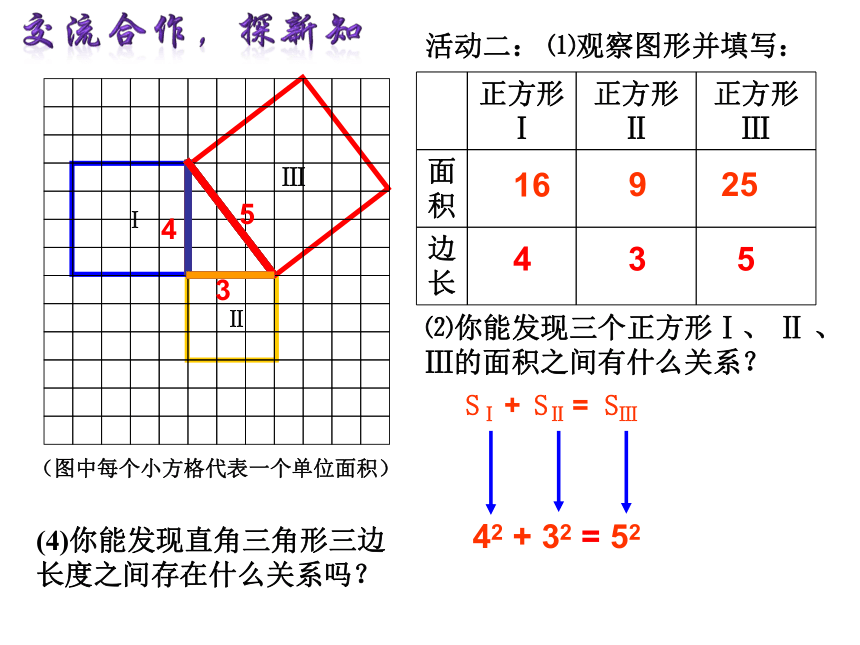
SⅠ= 42 SⅡ= 32 SⅢ = 52活动二: ⑴观察图形并填写:⑵你能发现三个正方形Ⅰ、 Ⅱ 、Ⅲ的面积之间有什么关系?⑶你能把正方形的面积用直角三角形的边长来表示吗?16925435(4)你能发现直角三角形三边长度之间存在什么关系吗?(图中每个小方格代表一个单位面积)43542 + 32 = 52
猜想:
直角三角形两直角边的平方和等于斜边的平方。勾股定理:
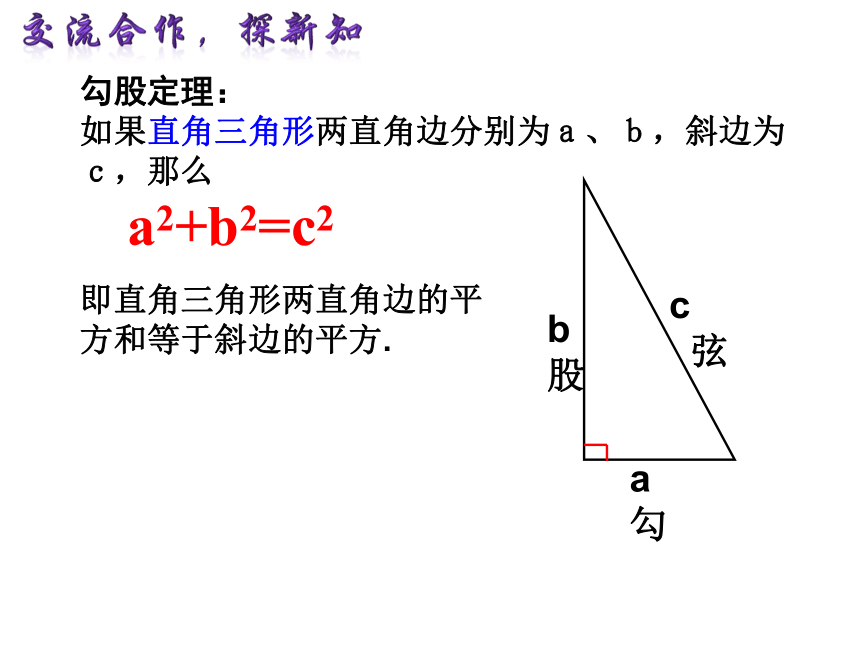
如果直角三角形两直角边分别为a、b,斜边为c,那么
a2+b2=c2
即直角三角形两直角边的平方和等于斜边的平方.
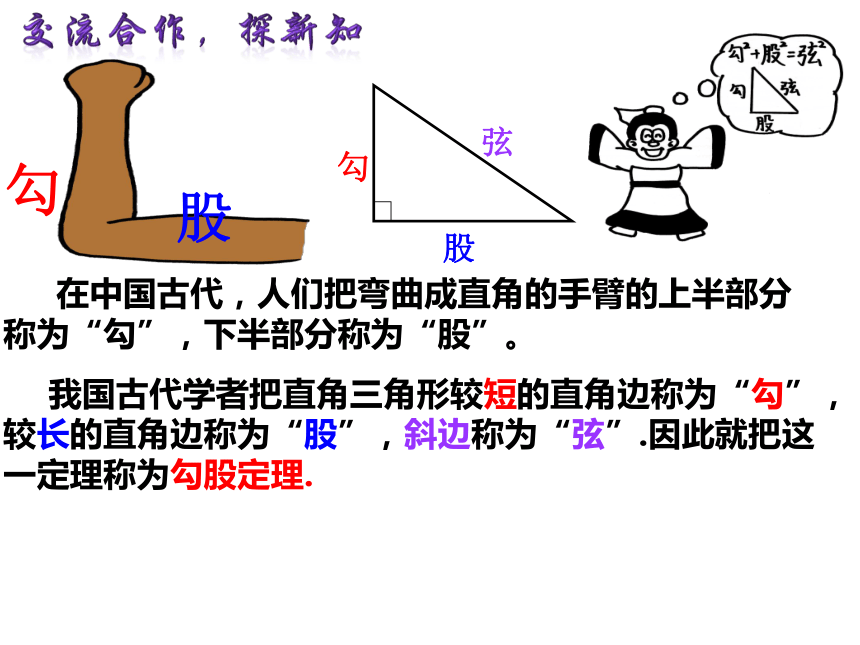
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
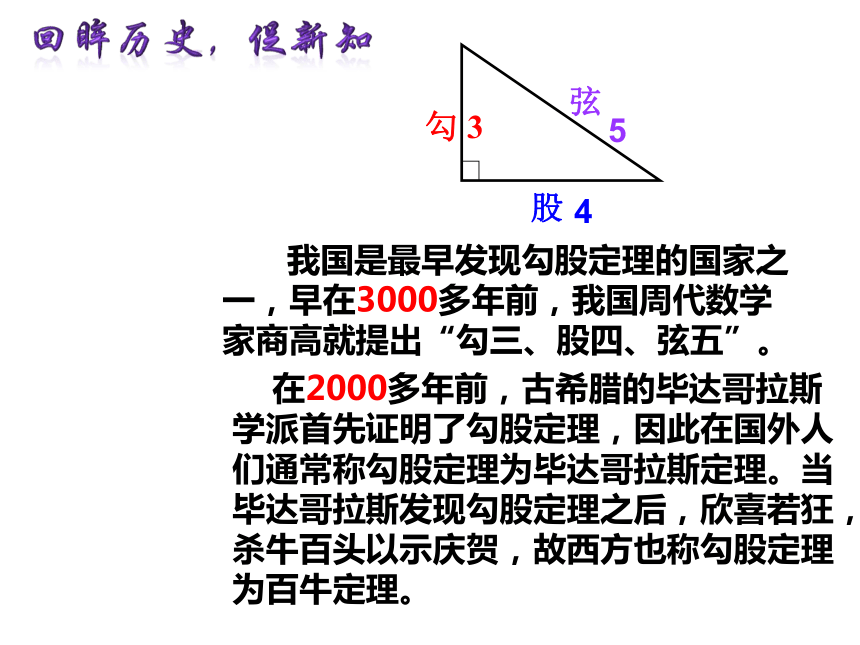
在2000多年前,古希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。当毕达哥拉斯发现勾股定理之后,欣喜若狂,杀牛百头以示庆贺,故西方也称勾股定理为百牛定理。 我国是最早发现勾股定理的国家之一,早在3000多年前,我国周代数学家商高就提出“勾三、股四、弦五”。541.下图是科普展品的两张设计图纸,其中正方形内的数表示这个正方形的面积,求字母所代表的正方形的面积.①②2.小明家刚刚买了一台52英寸的液晶电视。小明量了电视机的屏幕后,发现屏幕40英寸长,30英寸宽,小明家的电视机尺寸合格吗?1.今天我们用什么方法探索出了勾股定理?3.直角三角形的三边有何特殊关系?作用是什么?2.我们用到了哪种数学方法解决的问题?一个思想——勾股定理——转化的数学思想——由特殊到一般的探索——中国人的自豪一次探索一份自豪一个定理 2、通过书籍和网络查阅有关资料,了解勾股定理的历史背景和意义,并收集勾股定量的证明方法,在班级内办一个有关勾股定理的世博会。1、P29 习题2.2 第1、2题A码头B码头1300米500米C 3.为保障世博期间的水
上交通安全,上海海事局
要求世博客渡船应尽可能
成直角穿越黄浦江,任何
时候不得在码头之间成
斜线态势穿越。已知如图,浦东A码头与浦西B码头的距离为1300米,某客渡船沿蓝线航行,若从A码头航行到直角C处为500米,求客渡船走直角的总航程是多少?A码头B码头1300米500米C 3.为保障世博期间的水
上交通安全,上海海事局
要求世博客渡船应尽可能
成直角穿越黄浦江,任何
时候不得在码头之间成
斜线态势穿越。已知如图,浦东A码头与浦西B码头的距离为1300米,某客渡船沿蓝线航行,若从A码头航行到直角C处为500米,求客渡船走直角的总航程是多少?A码头B码头1300米500米C解:在Rt△ABC中,
由勾股定理可得
AB2=BC2+AC2,
13002=BC2+5002,
所以BC2=12002,即BC=1200. AC+BC=500+1200=1700(米) .
答:客渡船走直角的总航程是1700.
1.今天我们用什么方法探索出了勾股定理?3.直角三角形的三边有何特殊关系?作用是什么?2.我们用到了哪种数学方法解决的问题?一个思想——勾股定理——由特殊到一般的探索——中国人的自豪一次探索一份自豪一个定理——转化的数学思想 2、通过书籍和网络查阅有关资料,了解勾股定理的历史背景和意义,并收集勾股定量的证明方法,在班级内办一个有关勾股定理的世博会。1、P29 习题2.2 第1、2题ⅠⅡⅢ1.数格子
2.割、补法数学方法:数学思想:转化
SⅡ =9
SⅢ =18活动一:SⅠ + SⅡ = SⅢ
SⅠ= 42 SⅡ= 32 SⅢ = 52活动二: ⑴观察图形并填写:⑵你能发现三个正方形Ⅰ、 Ⅱ 、Ⅲ的面积之间有什么关系?⑶你能把正方形的面积用直角三角形的边长来表示吗?16925435(4)你能发现直角三角形三边长度之间存在什么关系吗?(图中每个小方格代表一个单位面积)43542 + 32 = 52
猜想:
直角三角形两直角边的平方和等于斜边的平方。勾股定理:
如果直角三角形两直角边分别为a、b,斜边为c,那么
a2+b2=c2
即直角三角形两直角边的平方和等于斜边的平方.
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”。
我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
在2000多年前,古希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。当毕达哥拉斯发现勾股定理之后,欣喜若狂,杀牛百头以示庆贺,故西方也称勾股定理为百牛定理。 我国是最早发现勾股定理的国家之一,早在3000多年前,我国周代数学家商高就提出“勾三、股四、弦五”。541.下图是科普展品的两张设计图纸,其中正方形内的数表示这个正方形的面积,求字母所代表的正方形的面积.①②2.小明家刚刚买了一台52英寸的液晶电视。小明量了电视机的屏幕后,发现屏幕40英寸长,30英寸宽,小明家的电视机尺寸合格吗?1.今天我们用什么方法探索出了勾股定理?3.直角三角形的三边有何特殊关系?作用是什么?2.我们用到了哪种数学方法解决的问题?一个思想——勾股定理——转化的数学思想——由特殊到一般的探索——中国人的自豪一次探索一份自豪一个定理 2、通过书籍和网络查阅有关资料,了解勾股定理的历史背景和意义,并收集勾股定量的证明方法,在班级内办一个有关勾股定理的世博会。1、P29 习题2.2 第1、2题A码头B码头1300米500米C 3.为保障世博期间的水
上交通安全,上海海事局
要求世博客渡船应尽可能
成直角穿越黄浦江,任何
时候不得在码头之间成
斜线态势穿越。已知如图,浦东A码头与浦西B码头的距离为1300米,某客渡船沿蓝线航行,若从A码头航行到直角C处为500米,求客渡船走直角的总航程是多少?A码头B码头1300米500米C 3.为保障世博期间的水
上交通安全,上海海事局
要求世博客渡船应尽可能
成直角穿越黄浦江,任何
时候不得在码头之间成
斜线态势穿越。已知如图,浦东A码头与浦西B码头的距离为1300米,某客渡船沿蓝线航行,若从A码头航行到直角C处为500米,求客渡船走直角的总航程是多少?A码头B码头1300米500米C解:在Rt△ABC中,
由勾股定理可得
AB2=BC2+AC2,
13002=BC2+5002,
所以BC2=12002,即BC=1200. AC+BC=500+1200=1700(米) .
答:客渡船走直角的总航程是1700.
1.今天我们用什么方法探索出了勾股定理?3.直角三角形的三边有何特殊关系?作用是什么?2.我们用到了哪种数学方法解决的问题?一个思想——勾股定理——由特殊到一般的探索——中国人的自豪一次探索一份自豪一个定理——转化的数学思想 2、通过书籍和网络查阅有关资料,了解勾股定理的历史背景和意义,并收集勾股定量的证明方法,在班级内办一个有关勾股定理的世博会。1、P29 习题2.2 第1、2题ⅠⅡⅢ1.数格子
2.割、补法数学方法:数学思想:转化
