函数的图象
图片预览






文档简介
课件22张PPT。函数的图象南侨中学 洪丽影1.已知: 与 的函数关系式为:求:(1)当 时, 的值。(2)当 时, 的值。 的图象(先填写下表,再描点、连线).
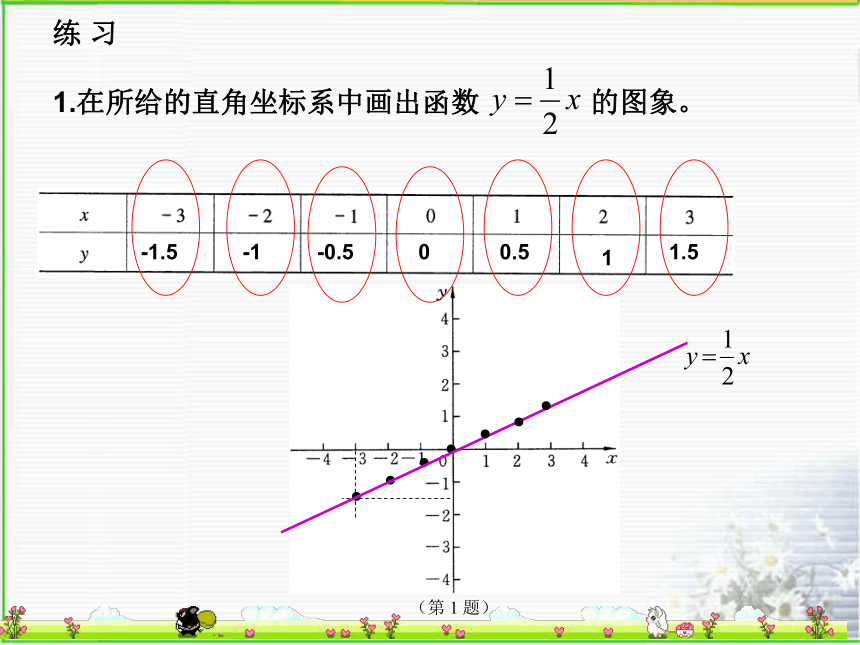
-1.5-1-0.500.511.5●●●●●●● 练 习
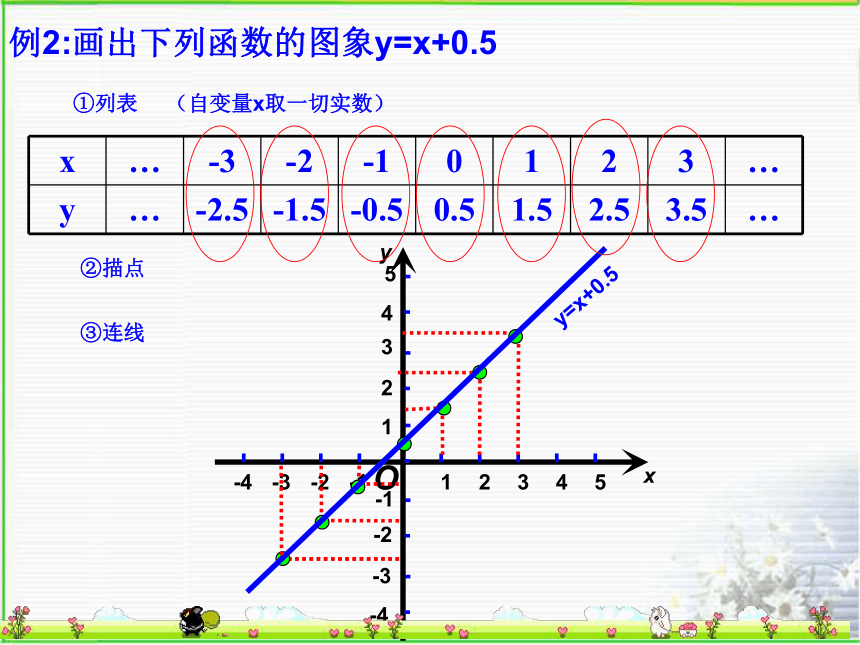
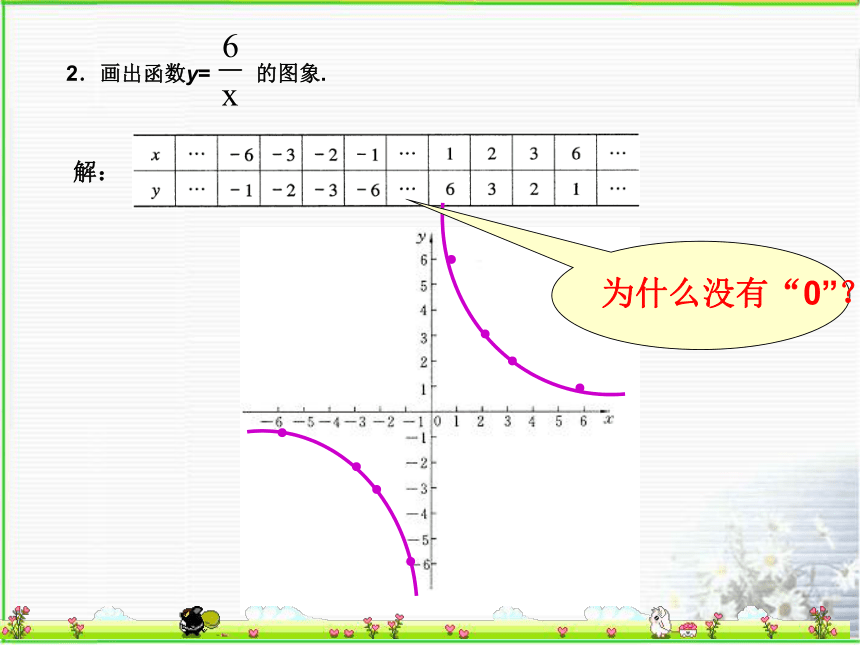
在所给的直角坐标系中画出函数 的图象。例2:画出下列函数的图象y=x+0.5①列表(自变量x取一切实数)②描点y=x+0.5③连线2.画出函数y=的图象.解:●●●●●●●●为什么没有“0”?判断下列各有序实数对是不是函数y= 的自变
量x与函数y的一对对应值,如果是,检验一下具有相应坐标的点是否在你所画的函数图象上:
(-2,-4),(3,-1),(1,3),(6,1).检测一次函数 执教者: 洪丽影探索一:看看我们身边的例子: 1、小张准备将平时的零用钱节约一些储存起来.他已存有50元,从现在起每个月节存12元.试写出小张的存款数y与从现在开始的月份数x之间的函数关系式
2、小红每天做5道数学课外练习,试写出小红所做题目的总数y和练习天数x之间的函数关系式_____________3、仓库内原有粉笔400盒,如果每个星期领出36盒,求仓库内余下的粉笔盒数Q与星期数t之间的函数关式________
4. 小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均车速是95千米/小时.已知A地直达北京的高速公路全程为570千米,小明想知道汽车从A地驶出后,距北京的路程y和汽车在高速公路上行驶的时间x有什么关系,以便根据时间估计自己和北京的距离.
比较下列各函数解析式,它们有哪些共同特征(1)等号两边的代数式都是整式;(2)自变量的次数是一次;(k,b都是常数,且 )y=50+12xy=5xQ=400-36tS=570-95t一次函数定义
一般地,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数 当b=0时,y=kx+b即y=kx,称为正比例函数. 所以说正比例函数是一种特 殊的一次函数.体验新知:例1:下列函数中,哪些是一次函数?
哪些又是正比例函数?并指出一次函
数中, k、b分别为多少?
一次函数正比例函数一次函数一次函数一次函数正比例函数练 习1.仓库内原有粉笔400盒,如果每个星期领出36盒,求仓库内余下的粉笔盒数Q与星期数t之间的函数关系式.2.今年植树节,同学们种的树苗高约1.80米.据介绍,这种树苗在10年内平均每年长高0.35米,求树高(米)与年数之间的函数关系式,并算一算4年后这些树约有多高.3.小徐的爸爸为小徐存了一份教育储蓄.首次存入1万元,以后每个月存入500元,存满3万元止.求存款数增长的规律.几个月后可存满全额?4.以上3道题中的函数有什么共同特点? Q=400-36t(0≤t≤11且为整数)y=1.80+0.35x(0≤x≤10且为整数)y=10000+500x(0≤x≤40且为整数)3.已知y与x-3成正比例,当x=4时, y=3 .(1)写出y与x之间的函数关系式;(2) y与x之间是什么函数关系式;(3)求x =2.5时, y的值解:(1) ∵ y与x-3成正比例∴可设y = k(x-3)又∵当x=4时, y=3 ∴3 = k(4-3)解得k =3∴y = 3(x-3) = 3x-9(2) y是x的一次函数;(3)当x =2.5时, y = 3×2.5-9 =-1.5(k ≠ 0)4.已知A、B两地相距30千米, B 、C两地相距48千米,某人骑自行车以每小时12千米的速度从A地出发,经过B地到达C地.设此人骑车时间为x(时)离B地距离为y(千米).(1)当此人在A、B两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;(2)当此人在B 、C两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;(1) y=30-12x,(0≤x ≤2.5)(2) y=12x -30,(2.5≤x ≤6.5)略解:分析:1.当a=____时,函数y=(a+2)x2a-3+6是一次函数.则该一次函数的解析式为_________2. 已知y与成正比例,
当 x=4时,y=3.
⑴ 写出y与x之间的函数关系式;
⑵ y与x之间是什么函数关系;
⑶ 求x=2.5时,y的值.作业布置
教材第47页 习题第1、2、3题例1:写出下列各题中x与y之间的关系式,并判断:是否为的一次函数?是否为正比函数?(1)汽车以60千米/时的速度匀速行驶,行驶路程y(千米)与行驶时间x(时)之间的关系;(2)圆的面积y(平方厘米)与它的半径x(厘米)之间的关系;(3)一棵树现在高50厘米,每个月长高2厘米,x月后这棵树的高度为y(厘米).谢谢大家
-1.5-1-0.500.511.5●●●●●●● 练 习
在所给的直角坐标系中画出函数 的图象。例2:画出下列函数的图象y=x+0.5①列表(自变量x取一切实数)②描点y=x+0.5③连线2.画出函数y=的图象.解:●●●●●●●●为什么没有“0”?判断下列各有序实数对是不是函数y= 的自变
量x与函数y的一对对应值,如果是,检验一下具有相应坐标的点是否在你所画的函数图象上:
(-2,-4),(3,-1),(1,3),(6,1).检测一次函数 执教者: 洪丽影探索一:看看我们身边的例子: 1、小张准备将平时的零用钱节约一些储存起来.他已存有50元,从现在起每个月节存12元.试写出小张的存款数y与从现在开始的月份数x之间的函数关系式
2、小红每天做5道数学课外练习,试写出小红所做题目的总数y和练习天数x之间的函数关系式_____________3、仓库内原有粉笔400盒,如果每个星期领出36盒,求仓库内余下的粉笔盒数Q与星期数t之间的函数关式________
4. 小明暑假第一次去北京.汽车驶上A地的高速公路后,小明观察里程碑,发现汽车的平均车速是95千米/小时.已知A地直达北京的高速公路全程为570千米,小明想知道汽车从A地驶出后,距北京的路程y和汽车在高速公路上行驶的时间x有什么关系,以便根据时间估计自己和北京的距离.
比较下列各函数解析式,它们有哪些共同特征(1)等号两边的代数式都是整式;(2)自变量的次数是一次;(k,b都是常数,且 )y=50+12xy=5xQ=400-36tS=570-95t一次函数定义
一般地,形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数 当b=0时,y=kx+b即y=kx,称为正比例函数. 所以说正比例函数是一种特 殊的一次函数.体验新知:例1:下列函数中,哪些是一次函数?
哪些又是正比例函数?并指出一次函
数中, k、b分别为多少?
一次函数正比例函数一次函数一次函数一次函数正比例函数练 习1.仓库内原有粉笔400盒,如果每个星期领出36盒,求仓库内余下的粉笔盒数Q与星期数t之间的函数关系式.2.今年植树节,同学们种的树苗高约1.80米.据介绍,这种树苗在10年内平均每年长高0.35米,求树高(米)与年数之间的函数关系式,并算一算4年后这些树约有多高.3.小徐的爸爸为小徐存了一份教育储蓄.首次存入1万元,以后每个月存入500元,存满3万元止.求存款数增长的规律.几个月后可存满全额?4.以上3道题中的函数有什么共同特点? Q=400-36t(0≤t≤11且为整数)y=1.80+0.35x(0≤x≤10且为整数)y=10000+500x(0≤x≤40且为整数)3.已知y与x-3成正比例,当x=4时, y=3 .(1)写出y与x之间的函数关系式;(2) y与x之间是什么函数关系式;(3)求x =2.5时, y的值解:(1) ∵ y与x-3成正比例∴可设y = k(x-3)又∵当x=4时, y=3 ∴3 = k(4-3)解得k =3∴y = 3(x-3) = 3x-9(2) y是x的一次函数;(3)当x =2.5时, y = 3×2.5-9 =-1.5(k ≠ 0)4.已知A、B两地相距30千米, B 、C两地相距48千米,某人骑自行车以每小时12千米的速度从A地出发,经过B地到达C地.设此人骑车时间为x(时)离B地距离为y(千米).(1)当此人在A、B两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;(2)当此人在B 、C两地之间时,求 y与x之间的函数关系式及自变量x的取值范围;(1) y=30-12x,(0≤x ≤2.5)(2) y=12x -30,(2.5≤x ≤6.5)略解:分析:1.当a=____时,函数y=(a+2)x2a-3+6是一次函数.则该一次函数的解析式为_________2. 已知y与成正比例,
当 x=4时,y=3.
⑴ 写出y与x之间的函数关系式;
⑵ y与x之间是什么函数关系;
⑶ 求x=2.5时,y的值.作业布置
教材第47页 习题第1、2、3题例1:写出下列各题中x与y之间的关系式,并判断:是否为的一次函数?是否为正比函数?(1)汽车以60千米/时的速度匀速行驶,行驶路程y(千米)与行驶时间x(时)之间的关系;(2)圆的面积y(平方厘米)与它的半径x(厘米)之间的关系;(3)一棵树现在高50厘米,每个月长高2厘米,x月后这棵树的高度为y(厘米).谢谢大家
