六年级下学期数学3.2.2圆锥的体积课件(共22张PPT)
文档属性
| 名称 | 六年级下学期数学3.2.2圆锥的体积课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 08:09:02 | ||
图片预览





文档简介
(共22张PPT)
圆锥的体积
圆锥的体积
说课
教材分析
教法学法
学情分析
教学过程
教学目标
板书设计
0
教学重难点
教法学法
引导发现法
采用多媒体辅助教学,让学生全程地参与教学的每一环节。
动手操作法
设疑激趣法
0
情境导入
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
圆柱公式复习
V柱=πr2h
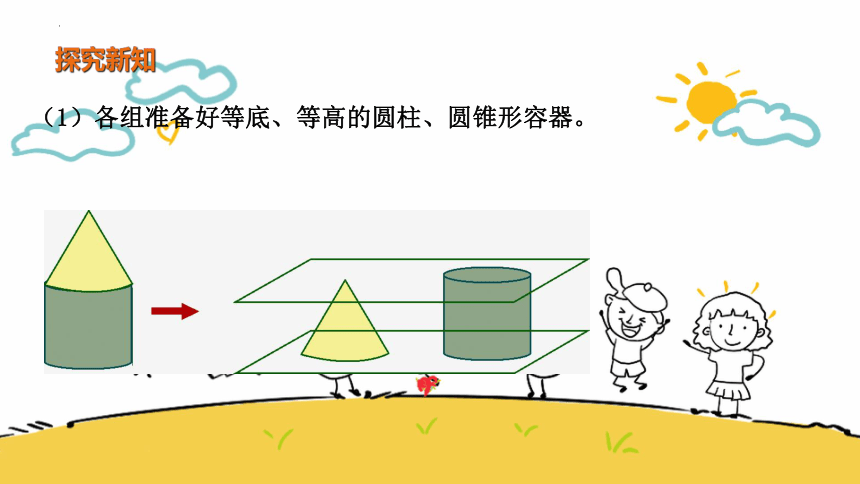
探究新知
(1)各组准备好等底、等高的圆柱、圆锥形容器。
思考:
1.任意圆锥和圆柱都可以吗?
2.对圆锥和圆柱的选取有什么要求呢?
小组活动,验证猜想。
圆柱和圆锥应等底等高。
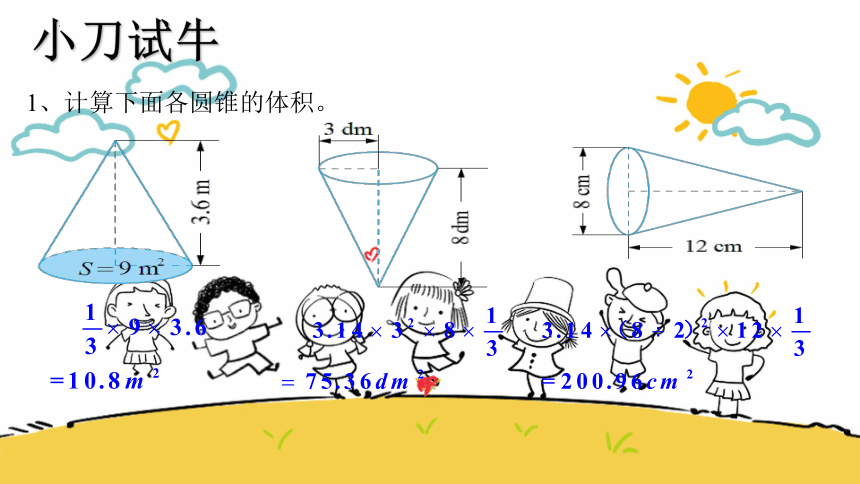
1、计算下面各圆锥的体积。
小刀试牛
探究新知
一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm 。
×19 ×12=76(cm )
3
1
圆柱的体积
圆锥的体积
介绍圆锥的底面和高
底面
高
(一条)
合作学习
1、合理猜想,指引方向
思考:选择哪种立体图形研究圆锥的体积更合适?
引导学生用实验法来探索圆锥体积的计算方法。
认真观察,它们之间的体积会有什么关系?
(出示圆柱、圆锥的教具)
圆锥的体积= ×
V = 3V
圆锥
圆柱
圆锥的体积等于与它等底等高圆柱体积的
底面积×高
Ⅴ = Ⅴ =
圆锥
圆柱
Sh
=
如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?
≈26.17(cm3)
巩固拓展
如图,把圆柱削成一个最大的圆锥。削去部分的体积是多少立方厘米?
10cm
15cm
3.14×(10÷2)2×15×
=3.14×25×15×
=785(cm3)
答:削去部分的体积是785cm3。
3
2
3
2
教师讲导
知道底面积和高就可以求出体积,但在实际中,底面积测量不出来时,还会出现什么情况呢?
①、已知圆锥的底面半径r和高h,如何求体积V?
②、已知圆锥的底面直径d和高h,如何求体积V?
③、已知圆锥的底面周长C和高h,如何求体积V?
1.想一想,议一议,说一说
【设计意图:避免学生死记公式,不能灵活运用,帮助学生将圆的半径、直径、周长及面积之间的关系联系起来。】
一个圆锥形沙堆,底面积是28.26m2,高是2.5m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
铺成的公路路面的体积等于圆锥形沙堆的体积。
圆锥体变成长方体,形状变了,前后体积没变。
精练强化
课堂练习
一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数。)
(1)铅锤底面积:
3.14×(4÷2)2=12.56 (cm2)
答:这个铅锤大约重163克 。
20.93×7.8≈163(g)
(3)铅锤的质量:
×12.56×5≈20.93(cm3)
(2)铅锤的体积:
同学们再见
圆锥的体积
圆锥的体积
说课
教材分析
教法学法
学情分析
教学过程
教学目标
板书设计
0
教学重难点
教法学法
引导发现法
采用多媒体辅助教学,让学生全程地参与教学的每一环节。
动手操作法
设疑激趣法
0
情境导入
我们已经学会计算圆柱的体积,请你回忆一下如何计算圆柱的体积?
圆柱公式复习
V柱=πr2h
探究新知
(1)各组准备好等底、等高的圆柱、圆锥形容器。
思考:
1.任意圆锥和圆柱都可以吗?
2.对圆锥和圆柱的选取有什么要求呢?
小组活动,验证猜想。
圆柱和圆锥应等底等高。
1、计算下面各圆锥的体积。
小刀试牛
探究新知
一个圆锥形的零件,底面积是19cm2,高是12cm,这个零件的体积是多少?
答:这个零件的体积是76cm 。
×19 ×12=76(cm )
3
1
圆柱的体积
圆锥的体积
介绍圆锥的底面和高
底面
高
(一条)
合作学习
1、合理猜想,指引方向
思考:选择哪种立体图形研究圆锥的体积更合适?
引导学生用实验法来探索圆锥体积的计算方法。
认真观察,它们之间的体积会有什么关系?
(出示圆柱、圆锥的教具)
圆锥的体积= ×
V = 3V
圆锥
圆柱
圆锥的体积等于与它等底等高圆柱体积的
底面积×高
Ⅴ = Ⅴ =
圆锥
圆柱
Sh
=
如图,测量中经常使用铅锤。这个铅锤的体积是
多少立方厘米?
≈26.17(cm3)
巩固拓展
如图,把圆柱削成一个最大的圆锥。削去部分的体积是多少立方厘米?
10cm
15cm
3.14×(10÷2)2×15×
=3.14×25×15×
=785(cm3)
答:削去部分的体积是785cm3。
3
2
3
2
教师讲导
知道底面积和高就可以求出体积,但在实际中,底面积测量不出来时,还会出现什么情况呢?
①、已知圆锥的底面半径r和高h,如何求体积V?
②、已知圆锥的底面直径d和高h,如何求体积V?
③、已知圆锥的底面周长C和高h,如何求体积V?
1.想一想,议一议,说一说
【设计意图:避免学生死记公式,不能灵活运用,帮助学生将圆的半径、直径、周长及面积之间的关系联系起来。】
一个圆锥形沙堆,底面积是28.26m2,高是2.5m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
铺成的公路路面的体积等于圆锥形沙堆的体积。
圆锥体变成长方体,形状变了,前后体积没变。
精练强化
课堂练习
一个用钢铸造成的圆锥形铅锤,底面直径是4cm,高5cm。每立方厘米钢大约重7.8g。这个铅锤重多少克?(得数保留整数。)
(1)铅锤底面积:
3.14×(4÷2)2=12.56 (cm2)
答:这个铅锤大约重163克 。
20.93×7.8≈163(g)
(3)铅锤的质量:
×12.56×5≈20.93(cm3)
(2)铅锤的体积:
同学们再见
