人教版六年级下学期数学3.1.2圆柱的表面积课件(共22张PPT)
文档属性
| 名称 | 人教版六年级下学期数学3.1.2圆柱的表面积课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 08:09:40 | ||
图片预览







文档简介
(共22张PPT)
圆柱的表面积
1、通过想象、操作等活动,理解“化曲面为平面”的计算方法
2、掌握圆柱侧面积与表面积的计算方法,应用于实际生活中
学习目标
一、预习自检环节:
1.我们学过哪些平面图形?
2.圆的周长和面积怎样求呢?
r=3cm d=( )=( )cm
c=( )=( )cm
s=( )=( )cm2
3.我们学过哪些立体图形?长方体和正方体
的表面积指什么?怎样计算?
4.生活中哪些物体是圆柱体呢?
6
2×3
2×3.14×3
18.84
3.14×32
28.26
-------立体图形
正方体
长方体
探究新知
圆柱的侧面积与展开后的长方形的面积有什么关系?
我们已经知道当圆柱的侧面沿高减开时,其展开图是一个长方形(或正方形)
圆柱基本特征:
底面
底面
高
侧面
圆柱上下两个面是圆柱的底面,为完全相同圆。
圆柱曲面是圆柱的侧面。
圆柱上下底之间的距离是圆柱的高
(圆柱的高有无数条)。
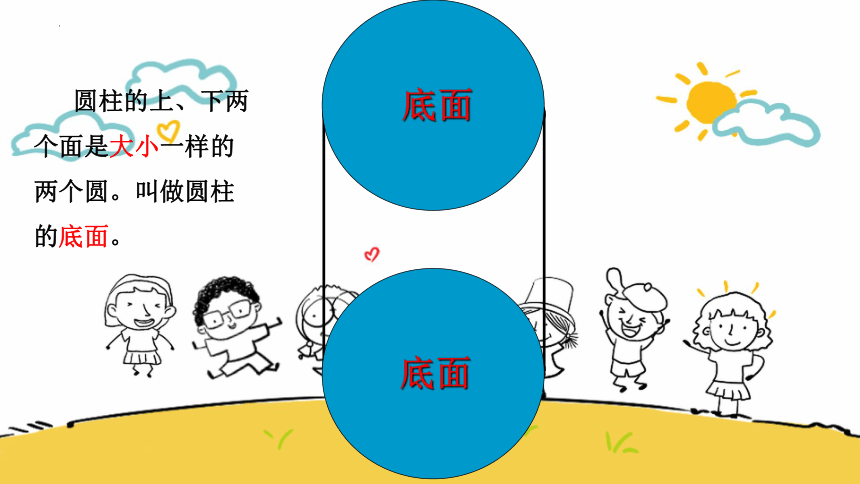
圆柱的上、下两个面是大小一样的两个圆。叫做圆柱的底面。
底面
底面
探究新知
1.求下面各圆柱的侧面积。
(1)底面周长是1.6m,高是0.7m。
侧面积=1.6×0.7=1.12(m )
(2)底面半径是3.2dm,高5dm。
侧面积=3.14×3.2×2×5=100.48(dm )
讨论:如果一段圆柱形的木头,截 成两截,它的表面积会有什么变化呢?
问题拓展
小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?(结果保留到个位)
侧面面积:
底面面积:
一共需要用的彩纸:
答:至少需要用274彩纸。
6cm
提示:
一顶帽子,上面是圆柱形,用黑布做,帽檐部分是一个圆环,用红布做。(单位:cm)请问:做这顶帽子红布用的多,还是黑布用的多?
底面圆的半径:
圆环的外径:10+10=20()
红布(圆环)面积:
黑布面积:
答:两种布用量一样多。
底面
底面
底面的周长
高
圆柱的侧面积=底面周长×高
圆柱的侧面积怎么计算呢?
(2)
A
B
C
D
2cm
(1)
答:长方形ABCD 如果以DC 边为轴旋转,会形成(1)号 圆柱。底面半径是2cm,高是1cm 。
转动长方形ABCD,生成什么图形?说说它们分别是以长方形的哪条边为轴旋转而成的,底面半径和高分别是多少?
1cm
长方形ABCD 如果以AD边为轴旋转 ,会形成(2)号圆柱。底面半径是1cm,高是2cm 。
巩固拓展
一台压路机的前轮是圆柱形的,轮宽2m,直径1.2m。前轮转动一周,压路的面积是多少平方米?
前轮转动一周,就是前轮的侧面积……
3.14×1.2×2=7.536(m2)
答:前轮转动一周,压路的面
积是7.536(m2)
1、修建一个圆柱形的水池,底面直径
是6m,深1.2m。在池的内壁与下底面
抹上水泥,抹水泥部分的面积是多少
平方米?
拓展延伸
1.转动长方形ABCD,生成右面的两个圆柱。说说它们分别是以长方形的哪条边为轴旋转而成的,底面半径和高分别是多少。
答:长方形ABCD如果以AB边为轴旋转,会形成(1)号圆
柱。底面半径是2cm,高是1cm 。
(1)
(2)
A
B
C
D
2cm
习题巩固
3、一个圆柱体的侧面展开是个边长9.42 cm的正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)
9.42×9.42 + 3.14×(9.42÷3.14÷2)2×2
=88.728 + 3.14×2.25×2
=102.858
≈102.86( cm2 )
答:这个圆柱体的表面积是102.86 cm2。
应用所学知识解决生活中实际问题。
创新与实践:
总结:掌握圆的表面积计算公式。
同学们再见
圆柱的表面积
1、通过想象、操作等活动,理解“化曲面为平面”的计算方法
2、掌握圆柱侧面积与表面积的计算方法,应用于实际生活中
学习目标
一、预习自检环节:
1.我们学过哪些平面图形?
2.圆的周长和面积怎样求呢?
r=3cm d=( )=( )cm
c=( )=( )cm
s=( )=( )cm2
3.我们学过哪些立体图形?长方体和正方体
的表面积指什么?怎样计算?
4.生活中哪些物体是圆柱体呢?
6
2×3
2×3.14×3
18.84
3.14×32
28.26
-------立体图形
正方体
长方体
探究新知
圆柱的侧面积与展开后的长方形的面积有什么关系?
我们已经知道当圆柱的侧面沿高减开时,其展开图是一个长方形(或正方形)
圆柱基本特征:
底面
底面
高
侧面
圆柱上下两个面是圆柱的底面,为完全相同圆。
圆柱曲面是圆柱的侧面。
圆柱上下底之间的距离是圆柱的高
(圆柱的高有无数条)。
圆柱的上、下两个面是大小一样的两个圆。叫做圆柱的底面。
底面
底面
探究新知
1.求下面各圆柱的侧面积。
(1)底面周长是1.6m,高是0.7m。
侧面积=1.6×0.7=1.12(m )
(2)底面半径是3.2dm,高5dm。
侧面积=3.14×3.2×2×5=100.48(dm )
讨论:如果一段圆柱形的木头,截 成两截,它的表面积会有什么变化呢?
问题拓展
小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?(结果保留到个位)
侧面面积:
底面面积:
一共需要用的彩纸:
答:至少需要用274彩纸。
6cm
提示:
一顶帽子,上面是圆柱形,用黑布做,帽檐部分是一个圆环,用红布做。(单位:cm)请问:做这顶帽子红布用的多,还是黑布用的多?
底面圆的半径:
圆环的外径:10+10=20()
红布(圆环)面积:
黑布面积:
答:两种布用量一样多。
底面
底面
底面的周长
高
圆柱的侧面积=底面周长×高
圆柱的侧面积怎么计算呢?
(2)
A
B
C
D
2cm
(1)
答:长方形ABCD 如果以DC 边为轴旋转,会形成(1)号 圆柱。底面半径是2cm,高是1cm 。
转动长方形ABCD,生成什么图形?说说它们分别是以长方形的哪条边为轴旋转而成的,底面半径和高分别是多少?
1cm
长方形ABCD 如果以AD边为轴旋转 ,会形成(2)号圆柱。底面半径是1cm,高是2cm 。
巩固拓展
一台压路机的前轮是圆柱形的,轮宽2m,直径1.2m。前轮转动一周,压路的面积是多少平方米?
前轮转动一周,就是前轮的侧面积……
3.14×1.2×2=7.536(m2)
答:前轮转动一周,压路的面
积是7.536(m2)
1、修建一个圆柱形的水池,底面直径
是6m,深1.2m。在池的内壁与下底面
抹上水泥,抹水泥部分的面积是多少
平方米?
拓展延伸
1.转动长方形ABCD,生成右面的两个圆柱。说说它们分别是以长方形的哪条边为轴旋转而成的,底面半径和高分别是多少。
答:长方形ABCD如果以AB边为轴旋转,会形成(1)号圆
柱。底面半径是2cm,高是1cm 。
(1)
(2)
A
B
C
D
2cm
习题巩固
3、一个圆柱体的侧面展开是个边长9.42 cm的正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)
9.42×9.42 + 3.14×(9.42÷3.14÷2)2×2
=88.728 + 3.14×2.25×2
=102.858
≈102.86( cm2 )
答:这个圆柱体的表面积是102.86 cm2。
应用所学知识解决生活中实际问题。
创新与实践:
总结:掌握圆的表面积计算公式。
同学们再见
