异面直线
图片预览




文档简介
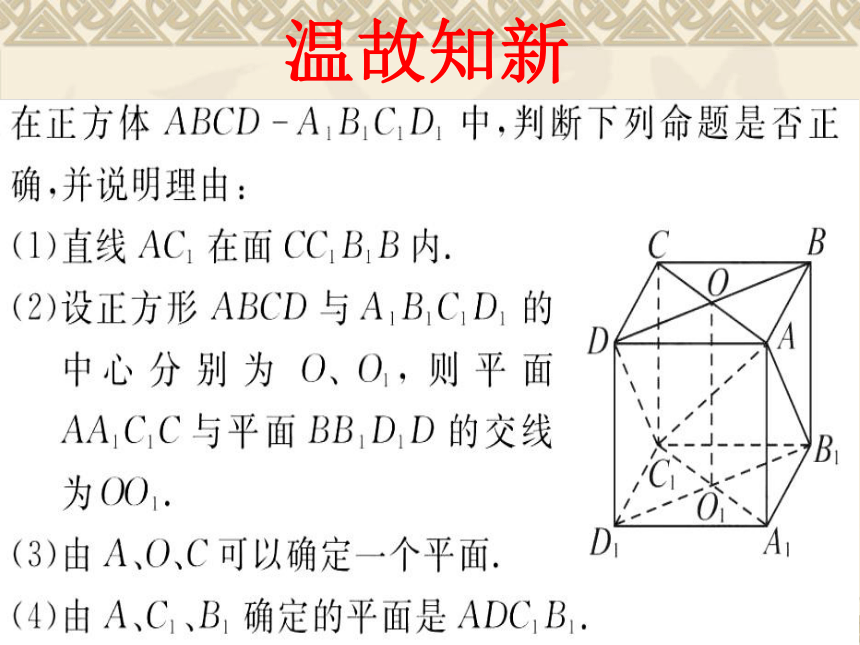
课件37张PPT。判断下列命题对错:
1、如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3、四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4、一条直线和一个点可以确定一个平面。( )
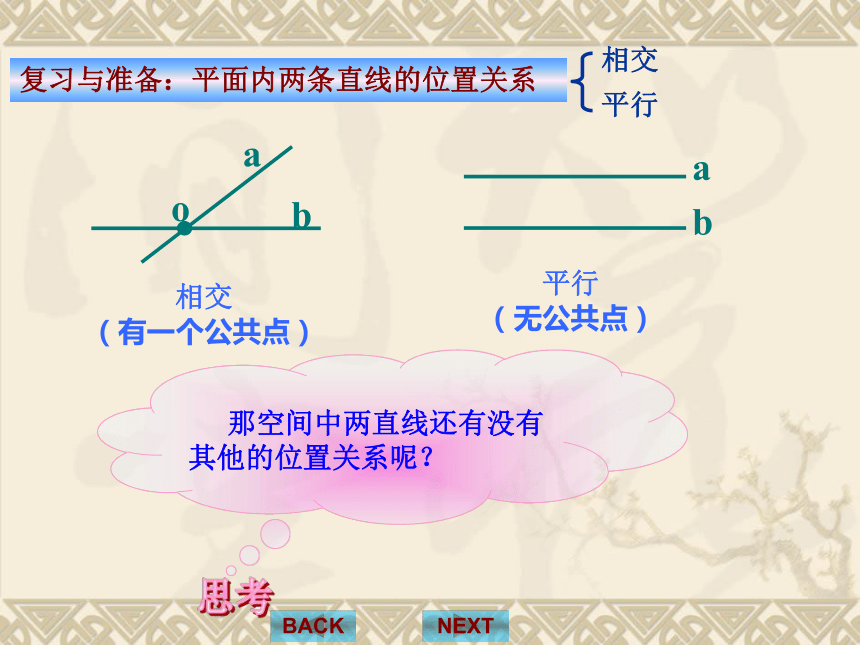
5、如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )×√×××温故知新温故知新 异 面 直 线新课标实验教材:人教版复习引入新课讲解例题选讲课堂小结相交
(有一个公共点)平行
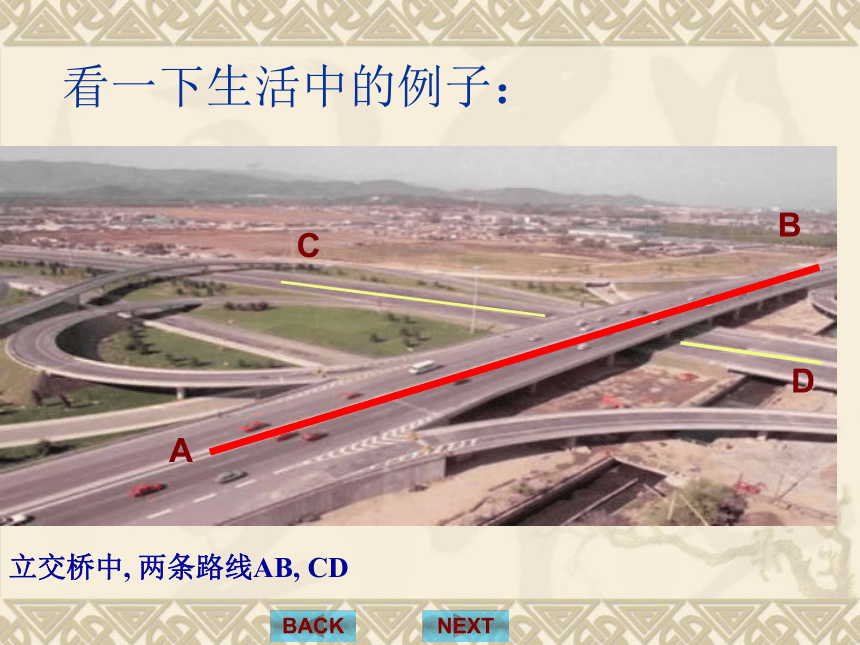
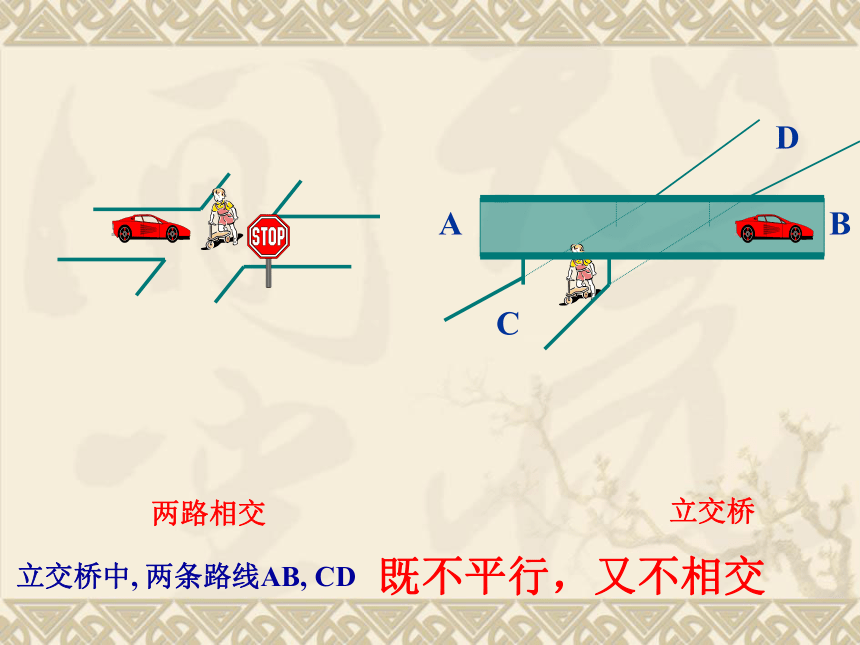
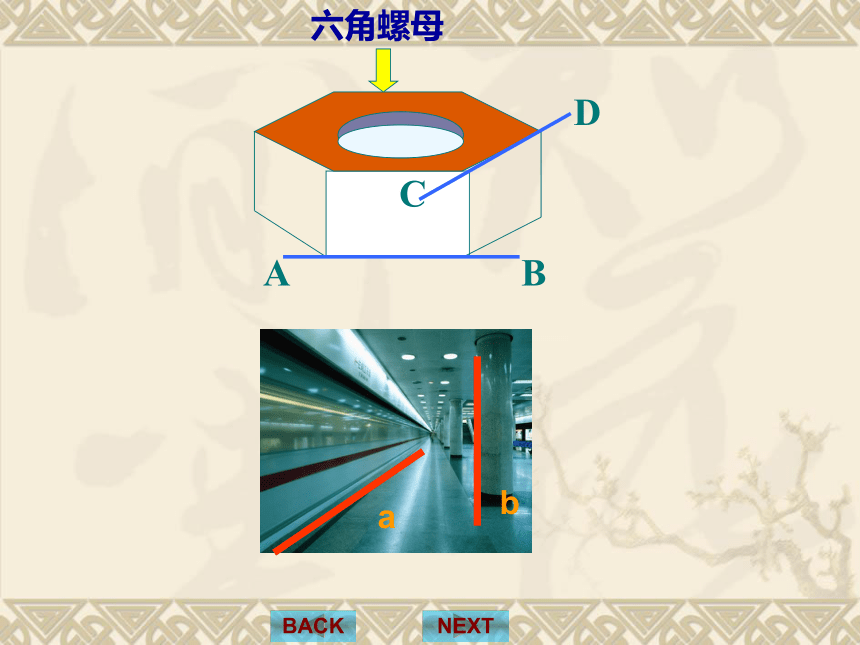
(无公共点)NEXTBACK复习与准备:平面内两条直线的位置关系看一下生活中的例子:立交桥中, 两条路线AB, CDNEXTBACKABCD两路相交立交桥立交桥中, 两条路线AB, CD既不平行,又不相交六角螺母NEXTBACKab思考一 2.平移a,b两条直线,它们能完全重合吗?NEXTBACKab1.直线a,b相交吗?不相交不平行3. 能否找到一个平面,
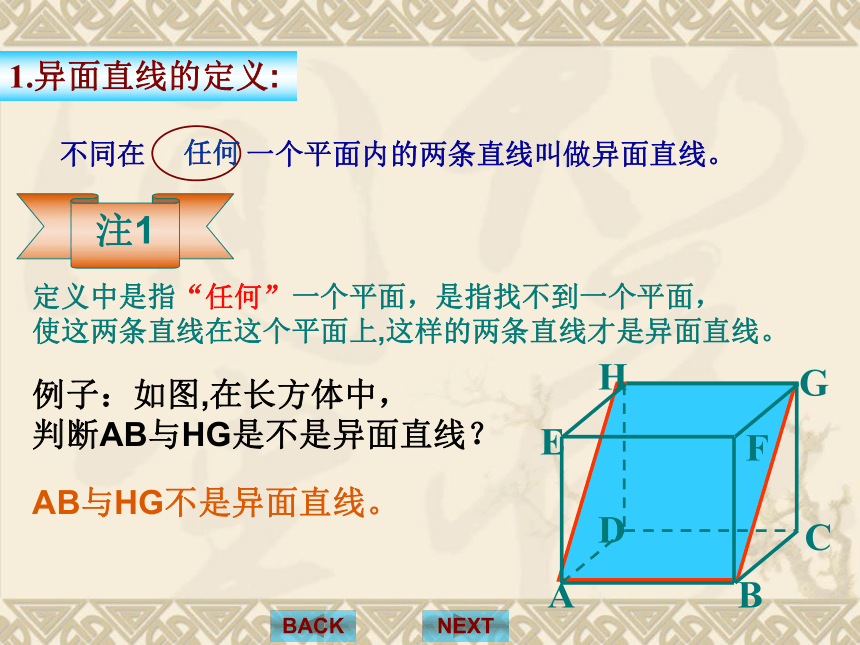
使得a,b两条直线都在这个平面内?NEXTBACK不同在 一个平面内的两条直线叫做异面直线。1.异面直线的定义:定义中是指“任何”一个平面,是指找不到一个平面,
使这两条直线在这个平面上,这样的两条直线才是异面直线。注1例子:如图,在长方体中,
判断AB与HG是不是异面直线?AB与HG不是异面直线。任何共面直线异面直线相交平行有且只有一个公共点没有公共点不同在任一平面,无公共点空间两条直线的位置关系
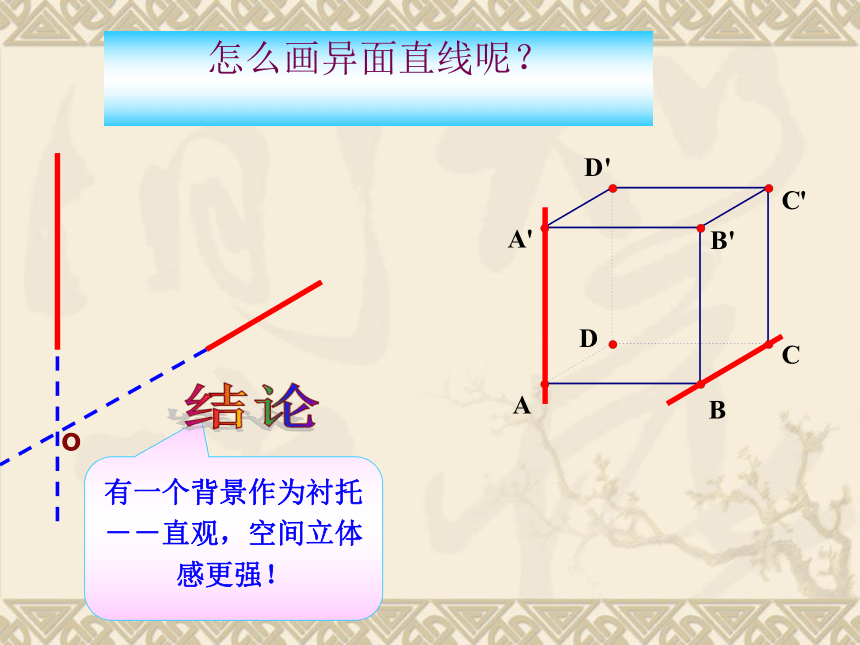
若两条直线没有公共点,则这两条直线异面或平行怎么画异面直线呢?
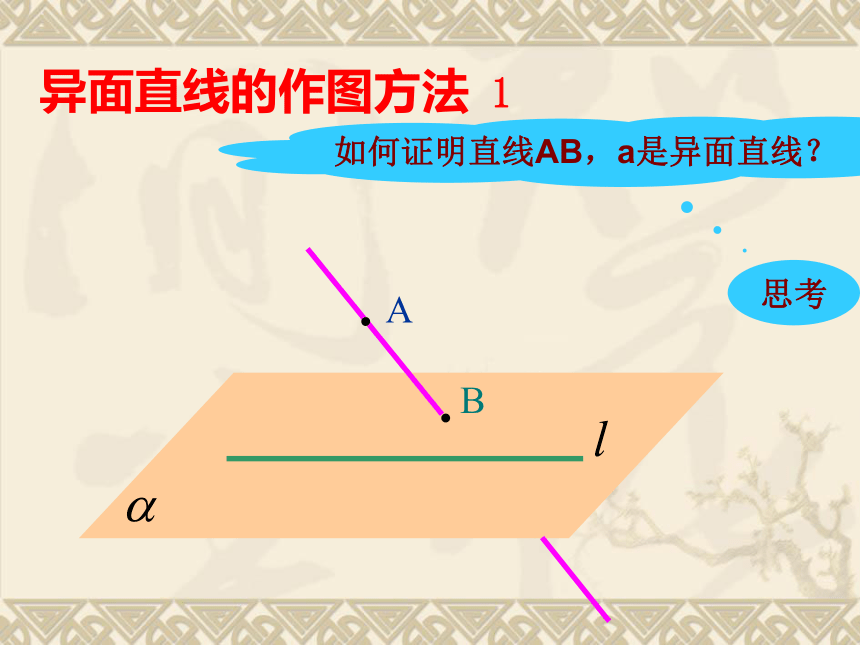
o异面直线的作图方法 1 AB如何证明直线AB,a是异面直线?思考异面直线的作图方法 2ab2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)1.平面内的一条直线和平面外的一条直线是异面直线。
答:错。
b例1.判断题1a4.例题a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线一定异面。判断题2NEXTBACK注2在不同平面内的两条直线不一定异面。例21)“a,b是异面直线”是指
① a∩b=Φ且a不平行于b;② a ? 平面?,b ? 平面 ?且a∩b=Φ ③ a ? 平面?,b ? 平面? ④ 不存在平面?,能使a ? ?且b ? ?成立
上述结论中,正确的是 ( )(A)①② (B)①③ (C)①④ (D)③④ C下图长方体中平行相交异面② BD 和FH是 直线① EC 和BH是 直线③EB和HG是 直线说出以下各对线段的位置关系?NEXTBACK例3O
方法二(特点) :两条直线 既不相交、又不平行.方法一 (利用定义):两条直线不同在任何一个平面内.2.判别异面直线的方法:NEXTBACKNEXTBACK5.课堂小结: 按平面基本性质分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点: 按公共点个数分相交直线无 公 共 点平行直线异面直线空间直线与直线之间的位置关系
方法二(特点) :两条直线 既不相交、又不平行.方法一 (利用定义):两条直线不同在任何一个平面内.2.判别异面直线的方法:NEXTBACK公理4:平行于同一条直线的两条直线互相平行注:
1、直线a,b,c 两两平行,可记为a // b // c 2、公理4所表述的性质,叫做空间平行线的传递性3、证明空间两直线平行 的方法:
(1) 定义法:一要证两直线在同一平面内;二要证两直线没有公共点(反证法)
(2) 公理法平行公理例2:如图,空间四边行ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.D变式:如果再加上条件AC=BD,那么四边形EFGH是什么图形? 立体问题平面化是解立体几何时最主要、最常用的一种方法。四边形ABCD是空间四边形,E、H分别是AB,AD的中点 ,F、G分别是CB,CD上的点,且
求证:四边形EFGH是梯形练习㈡:在平面内, 我们可以证明 “ 如果一个角的两边与另一个角的
两边分别平行,那么这两个角相等或互补 ”.空间中这一结
论是否仍然成立呢?定理(等角定理):空间中,如果两个角的两边分别对应平行,
那么这两个角相等或互补.观察 :如图所示,长方体ABCD-A1B1C1D1中, ∠ADC与∠A1D1C1 ,
∠ADC与∠A1B1C1两边分别对应平行,这两组角的大小
关系如何?NEXTBACK等角定理1:如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补等角定理2:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等等角定理3.异面直线所成的角 在平面内,两条直线相交成四
个角, 其中不大于90度的角称为它
们的夹角, 用以刻画两直线的错开
程度, 如图. 在空间,如图所示, 正方体ABCD-EFGH中, 异面直线AB与HF的错开程度可以怎样来刻画呢?(2)问题提出(1)复习回顾NEXTBACK定义:直线a、b为异面直线,经过空间任一点O,分别引a′∥a,b′∥b,则相交直线a′,b′所成的锐角(或直角)叫做两条异面直线a、b所成的角(或夹角)两条异面直线所成的角注1:异面直线a、b所成角,只与a、b的相互位置有关,而与点O位置无关注2:一般常把点O取在直线a或b上注3:异面直线所成角的取值范围:如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角。?任选若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 平移4、两条异面直线所成的角一作(找)二证三求脑筋急转弯:(1)若果两条平行线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?( )(2) 垂直同一条直线的两条直线是否平行?( )(3)与同一条直线所成的角相等,两直线平行吗?( )(4)存在与两条异面直线都平行的第三直线对吗?( )(5) 与两条异面直线都相交的直线有几条?( )(6) 与两条异面直线都垂直的直线有几条?( )(7) 与两条异面直线都垂直且相交的直线有几条?( )√×××无数无数唯一例1、如图表示一个正方体(1)图中哪些棱所在的直线与直线BA1成异面直线(2)求直线BA1与CC1的夹角的度数(3)哪些棱所在的直线与直线AA1垂直典例剖析例2、如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值CBADA1B1C1D1典例剖析aaNEXTBACK 如图,已知长方体ABCD-EFGH中, AB = , AD = , AE = 2
(1)求BC 和EG 所成的角是多少度?
(2)求AE 和BG 所成的角是多少度?解答:练习小结
1、如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2、将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3、四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4、一条直线和一个点可以确定一个平面。( )
5、如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )×√×××温故知新温故知新 异 面 直 线新课标实验教材:人教版复习引入新课讲解例题选讲课堂小结相交
(有一个公共点)平行
(无公共点)NEXTBACK复习与准备:平面内两条直线的位置关系看一下生活中的例子:立交桥中, 两条路线AB, CDNEXTBACKABCD两路相交立交桥立交桥中, 两条路线AB, CD既不平行,又不相交六角螺母NEXTBACKab思考一 2.平移a,b两条直线,它们能完全重合吗?NEXTBACKab1.直线a,b相交吗?不相交不平行3. 能否找到一个平面,
使得a,b两条直线都在这个平面内?NEXTBACK不同在 一个平面内的两条直线叫做异面直线。1.异面直线的定义:定义中是指“任何”一个平面,是指找不到一个平面,
使这两条直线在这个平面上,这样的两条直线才是异面直线。注1例子:如图,在长方体中,
判断AB与HG是不是异面直线?AB与HG不是异面直线。任何共面直线异面直线相交平行有且只有一个公共点没有公共点不同在任一平面,无公共点空间两条直线的位置关系
若两条直线没有公共点,则这两条直线异面或平行怎么画异面直线呢?
o异面直线的作图方法 1 AB如何证明直线AB,a是异面直线?思考异面直线的作图方法 2ab2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)1.平面内的一条直线和平面外的一条直线是异面直线。
答:错。
b例1.判断题1a4.例题a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线一定异面。判断题2NEXTBACK注2在不同平面内的两条直线不一定异面。例21)“a,b是异面直线”是指
① a∩b=Φ且a不平行于b;② a ? 平面?,b ? 平面 ?且a∩b=Φ ③ a ? 平面?,b ? 平面? ④ 不存在平面?,能使a ? ?且b ? ?成立
上述结论中,正确的是 ( )(A)①② (B)①③ (C)①④ (D)③④ C下图长方体中平行相交异面② BD 和FH是 直线① EC 和BH是 直线③EB和HG是 直线说出以下各对线段的位置关系?NEXTBACK例3O
方法二(特点) :两条直线 既不相交、又不平行.方法一 (利用定义):两条直线不同在任何一个平面内.2.判别异面直线的方法:NEXTBACKNEXTBACK5.课堂小结: 按平面基本性质分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点: 按公共点个数分相交直线无 公 共 点平行直线异面直线空间直线与直线之间的位置关系
方法二(特点) :两条直线 既不相交、又不平行.方法一 (利用定义):两条直线不同在任何一个平面内.2.判别异面直线的方法:NEXTBACK公理4:平行于同一条直线的两条直线互相平行注:
1、直线a,b,c 两两平行,可记为a // b // c 2、公理4所表述的性质,叫做空间平行线的传递性3、证明空间两直线平行 的方法:
(1) 定义法:一要证两直线在同一平面内;二要证两直线没有公共点(反证法)
(2) 公理法平行公理例2:如图,空间四边行ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.D变式:如果再加上条件AC=BD,那么四边形EFGH是什么图形? 立体问题平面化是解立体几何时最主要、最常用的一种方法。四边形ABCD是空间四边形,E、H分别是AB,AD的中点 ,F、G分别是CB,CD上的点,且
求证:四边形EFGH是梯形练习㈡:在平面内, 我们可以证明 “ 如果一个角的两边与另一个角的
两边分别平行,那么这两个角相等或互补 ”.空间中这一结
论是否仍然成立呢?定理(等角定理):空间中,如果两个角的两边分别对应平行,
那么这两个角相等或互补.观察 :如图所示,长方体ABCD-A1B1C1D1中, ∠ADC与∠A1D1C1 ,
∠ADC与∠A1B1C1两边分别对应平行,这两组角的大小
关系如何?NEXTBACK等角定理1:如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补等角定理2:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等等角定理3.异面直线所成的角 在平面内,两条直线相交成四
个角, 其中不大于90度的角称为它
们的夹角, 用以刻画两直线的错开
程度, 如图. 在空间,如图所示, 正方体ABCD-EFGH中, 异面直线AB与HF的错开程度可以怎样来刻画呢?(2)问题提出(1)复习回顾NEXTBACK定义:直线a、b为异面直线,经过空间任一点O,分别引a′∥a,b′∥b,则相交直线a′,b′所成的锐角(或直角)叫做两条异面直线a、b所成的角(或夹角)两条异面直线所成的角注1:异面直线a、b所成角,只与a、b的相互位置有关,而与点O位置无关注2:一般常把点O取在直线a或b上注3:异面直线所成角的取值范围:如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角。?任选若两条异面直线所成角为90°,则称它们互相垂直。异面直线a与b垂直也记作a⊥b异面直线所成角θ的取值范围: 平移4、两条异面直线所成的角一作(找)二证三求脑筋急转弯:(1)若果两条平行线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?( )(2) 垂直同一条直线的两条直线是否平行?( )(3)与同一条直线所成的角相等,两直线平行吗?( )(4)存在与两条异面直线都平行的第三直线对吗?( )(5) 与两条异面直线都相交的直线有几条?( )(6) 与两条异面直线都垂直的直线有几条?( )(7) 与两条异面直线都垂直且相交的直线有几条?( )√×××无数无数唯一例1、如图表示一个正方体(1)图中哪些棱所在的直线与直线BA1成异面直线(2)求直线BA1与CC1的夹角的度数(3)哪些棱所在的直线与直线AA1垂直典例剖析例2、如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值CBADA1B1C1D1典例剖析aaNEXTBACK 如图,已知长方体ABCD-EFGH中, AB = , AD = , AE = 2
(1)求BC 和EG 所成的角是多少度?
(2)求AE 和BG 所成的角是多少度?解答:练习小结
