沪科版七年级下册 8.1 幂的运算课件(共23张PPT)
文档属性
| 名称 | 沪科版七年级下册 8.1 幂的运算课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 349.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
同底数幂的乘法
8.1 幂的运算
我国首台千万亿次超级计算机系统“天河一号”计算机每秒可计算2.57×1015次运算。它工作1h(3.6×103s)共进行了多少次运算?
2.57×1015 × 3.6×103s
=2.57×3.6×1015×103
=?
如何简洁地把结果表示出来呢?
试试看,你还记得吗?
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
3、a · a · · · · · · a = a( )
n个
3
5
n
an
底数
指数
幂
探索发现:
=27 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=57
23 ×24
53×54
=(2 ×2 ×2) ×(2 ×2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 ×2 ×2 (乘法结合律)
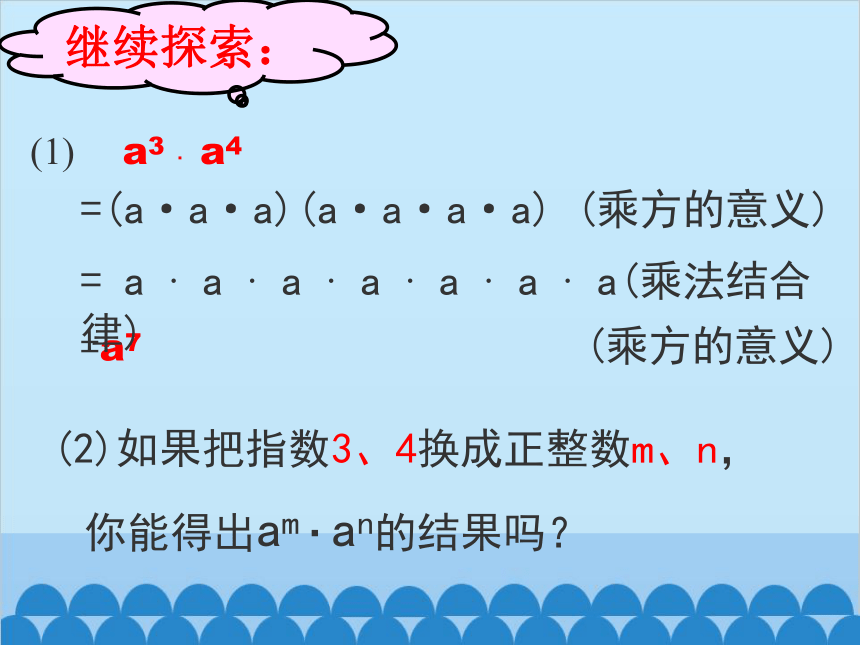
(2)如果把指数3、4换成正整数m、n,你能得出am·an的结果吗?
=a7 (乘方的意义)
继续探索:
(1) a3 · a4
=(a·a·a)(a·a·a·a) (乘方的意义)
= a · a · a · a · a · a · a(乘法结合律)
= am+n
n个
m个
(a · a · a…… · a)(a · a · a…… · a)
m+n个
= a · a · a…… · a
am · an
=
同底数幂相乘,底数不变,指数相加。
am · an = am+n
(m、n为正整数)
我国首台千万亿次超级计算机系统“天河一号”计算机每秒可计算2.57×1015次运算。它工作1h(3.6×103s)共进行了多少次运算?
2.57×1015 × 3.6×103s
=2.57×3.6×1015×103
=9.252×1018
例1:计算
想想看!
am · an · ap = ( m、n、p为正整数)
am · an · ap
= am+n · ap
= am+n+p
am · an · ap = am+n+p
( m、n、p为正整数)
例1:计算
计算:
① 102×105 =
② a3 · a7 =
③ x · x5 · x7 =
题组练习一:
107
a10
x13
计 算:
① 32×3m =
② 5m· 5n =
③ x3 · xn+1 =
④y · yn+2 · yn+4 =
题组练习二:
3m+2
5m+n
y2n+7
Xn+4
计 算:(结果写成幂的形式)
① (- 2)4×(- 2)5 =
②( ) 3 ×( ) 2 =
③ (a+b)2 · (a+b)5 =
题组练习三:
(- 2)9
(a+b)7
( ) 5
加油啊!
计 算:
① 23×2( ) = 27
② a( ) · a2 = a8
③ bm · b( ) = bm+n
题组练习四:
4
6
n
你真棒!
判断下列计算是否正确,并简要说明理由:
① x · x2= x2
② a+a2 = a3
③ y3 · y3= y9
④ b3+b3 = b6
(×)
(×)
(×)
(×)
题组练习五:
∵am · an = am+n (m、n为正整数)
∴ am+n = am · an (m、n为正整数)
逆向应用:
已知:am=2, an=3.
求am+n =?
动脑筋
解: am+n = am · an
=2 × 3=6
拓展训练,深化提高
1、计算:(结果写成幂的形式)
23 + 23=
2 × 23
= 24
34 × 27=
34 × 33
=37
b2· b3+b · b4 =
b5 + b5
=2b5
今天,我们学到了什么?
同底数幂的乘法:
am · an = am+n (m、n为正整数)
小结:
同底数幂相乘,底数不变,指数相加。
根据乘方的意义及同底数幂的乘法填空:
(1) (23 )2 = 23 × 23 =2( )
(2) (am )n = a( ) (m、n为正整数)
课后探索
作业:
1、课本:P.54 习题8.1 1;
2、基础训练
同底数幂的乘法
8.1 幂的运算
我国首台千万亿次超级计算机系统“天河一号”计算机每秒可计算2.57×1015次运算。它工作1h(3.6×103s)共进行了多少次运算?
2.57×1015 × 3.6×103s
=2.57×3.6×1015×103
=?
如何简洁地把结果表示出来呢?
试试看,你还记得吗?
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
3、a · a · · · · · · a = a( )
n个
3
5
n
an
底数
指数
幂
探索发现:
=27 (乘方的意义)
=(5 × 5 × 5) ×(5 × 5 × 5 × 5)
= 5 × 5 × 5 × 5 × 5 × 5 × 5
=57
23 ×24
53×54
=(2 ×2 ×2) ×(2 ×2 ×2 ×2) (乘方的意义)
= 2 ×2 ×2 ×2 × 2 ×2 ×2 (乘法结合律)
(2)如果把指数3、4换成正整数m、n,你能得出am·an的结果吗?
=a7 (乘方的意义)
继续探索:
(1) a3 · a4
=(a·a·a)(a·a·a·a) (乘方的意义)
= a · a · a · a · a · a · a(乘法结合律)
= am+n
n个
m个
(a · a · a…… · a)(a · a · a…… · a)
m+n个
= a · a · a…… · a
am · an
=
同底数幂相乘,底数不变,指数相加。
am · an = am+n
(m、n为正整数)
我国首台千万亿次超级计算机系统“天河一号”计算机每秒可计算2.57×1015次运算。它工作1h(3.6×103s)共进行了多少次运算?
2.57×1015 × 3.6×103s
=2.57×3.6×1015×103
=9.252×1018
例1:计算
想想看!
am · an · ap = ( m、n、p为正整数)
am · an · ap
= am+n · ap
= am+n+p
am · an · ap = am+n+p
( m、n、p为正整数)
例1:计算
计算:
① 102×105 =
② a3 · a7 =
③ x · x5 · x7 =
题组练习一:
107
a10
x13
计 算:
① 32×3m =
② 5m· 5n =
③ x3 · xn+1 =
④y · yn+2 · yn+4 =
题组练习二:
3m+2
5m+n
y2n+7
Xn+4
计 算:(结果写成幂的形式)
① (- 2)4×(- 2)5 =
②( ) 3 ×( ) 2 =
③ (a+b)2 · (a+b)5 =
题组练习三:
(- 2)9
(a+b)7
( ) 5
加油啊!
计 算:
① 23×2( ) = 27
② a( ) · a2 = a8
③ bm · b( ) = bm+n
题组练习四:
4
6
n
你真棒!
判断下列计算是否正确,并简要说明理由:
① x · x2= x2
② a+a2 = a3
③ y3 · y3= y9
④ b3+b3 = b6
(×)
(×)
(×)
(×)
题组练习五:
∵am · an = am+n (m、n为正整数)
∴ am+n = am · an (m、n为正整数)
逆向应用:
已知:am=2, an=3.
求am+n =?
动脑筋
解: am+n = am · an
=2 × 3=6
拓展训练,深化提高
1、计算:(结果写成幂的形式)
23 + 23=
2 × 23
= 24
34 × 27=
34 × 33
=37
b2· b3+b · b4 =
b5 + b5
=2b5
今天,我们学到了什么?
同底数幂的乘法:
am · an = am+n (m、n为正整数)
小结:
同底数幂相乘,底数不变,指数相加。
根据乘方的意义及同底数幂的乘法填空:
(1) (23 )2 = 23 × 23 =2( )
(2) (am )n = a( ) (m、n为正整数)
课后探索
作业:
1、课本:P.54 习题8.1 1;
2、基础训练
