六年级下学期数学6.1.4比和比例课件(共18张PPT)
文档属性
| 名称 | 六年级下学期数学6.1.4比和比例课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
比和比例
﹙二﹚汇报交流
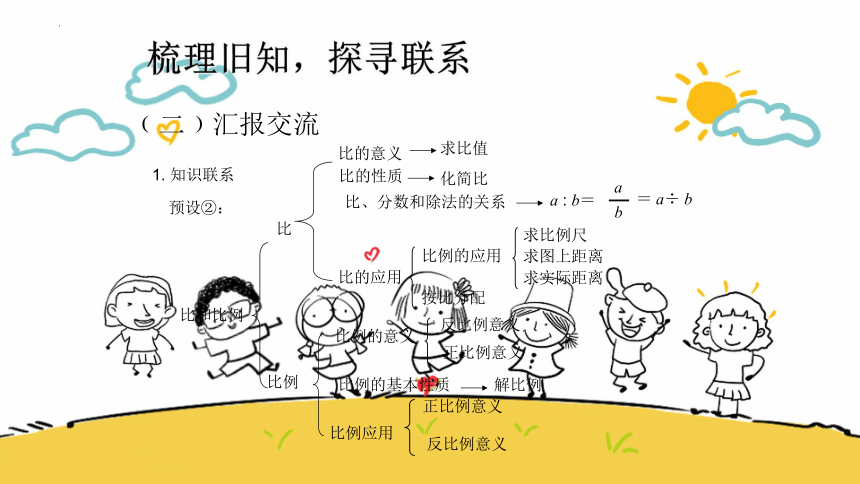
梳理旧知,探寻联系
1. 知识联系
预设②:
比例
比例应用
反比例意义
比和比例
比
求比值
比的性质
比的意义
化简比
比、分数和除法的关系
比的应用
a : b=
b
a
= a÷ b
比例的应用
按比分配
求比例尺
求图上距离
求实际距离
比例的意义
正比例意义
比例的基本性质
解比例
正比例意义
反比例意义
绿色圃中小学教育网http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育网http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
下面五个式子,哪几个是比,哪几个是比例?
(1)36:24
(2)2.4:1.6=60:40
(4)1.4:20=28:40
(3)5.2:0.13
(5)
5
8
:
3
2
(1)36:24
(3)5.2:0.13
(5)
5
8
:
3
2
(2)2.4:1.6=60:40
(4)1.4:20=28:40
判断比和比例
比
比例
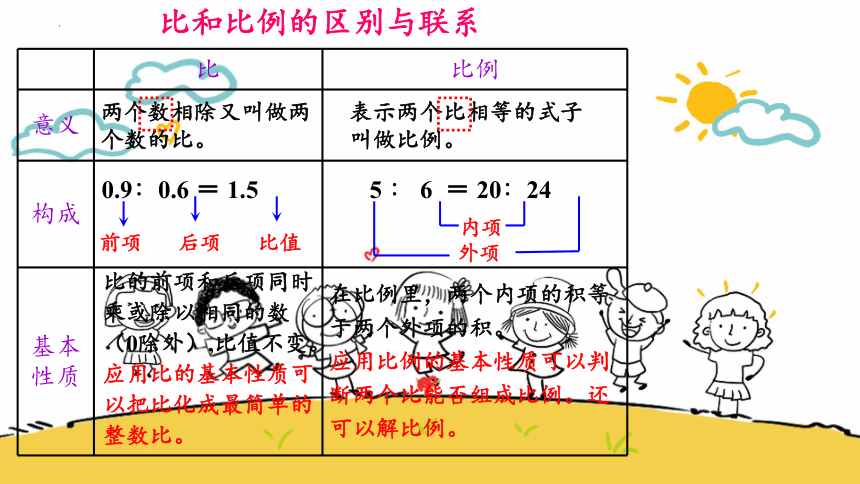
比和比例的区别与联系
比 比例
意义
构成
基本性质
两个数相除又叫做两
个数的比。
表示两个比相等的式子
叫做比例。
0.9∶0.6 = 1.5
前项
后项
比值
5 ∶ 6 = 20∶24
内项
外项
比的前项和后项同时乘或除以相同的数(0除外),比值不变。应用比的基本性质可以把比化成最简单的整数比。
在比例里,两个内项的积等于两个外项的积。
应用比例的基本性质可以判断两个比能否组成比例。还可以解比例。
1.比和比例的区别?比和比值意义?
2.比和比例基本性质的区别?
3.比例基本性质的作用?比的基本性质的作用?
4.比各部分的名称?比例各部分的名称?
关于比和比例你想说什么?
一.探索与交流
正比例图
36:24
24:16
18:12
12:8
3:2
0
3
6
9
12
15
18
21
24
33
27
30
36
2
4
6
8
10
12
16
22
14
20
18
24
(3,2)
(12,8)
(18,12)
(24,16)
(36,24)
我会判
下面各题中的两个量是不是成比例?如果成比例,成什么比例?
1.全班人数一定,出勤人数和缺勤人数。( )
2.三角形的面积一定,它的底和高。( )
3.正方体一个面的面积和它的表面积。( )
4.圆的面积和半径。( )
不成比例
成反比例
成正比例
不成比例
1.什么是求比值?结果是什么形式的?
2.什么是化简比?结果又是什么形式的?
关于求比值和化简比你分得清楚吗?
三.探索与交流
小结:刚才同学们从知识内在联系和区别两方面梳理了比和比例的知识。
想必大家又有了新的收获。
提问4:比、比例的基本性质有什么用途呢?
预设:
①比的基本性质可以帮助我们把比化成最简单的整数比。
②比例的基本性质可以帮助我们解比例。
梳理旧知,探寻联系
汇报交流
出示练习:
化简比:
解比例:
3
2
2∶
7
2
4
1
∶x = ∶2
绿色圃中小学教育网http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育网http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
选择题。
1、实际距离一定,图上距离和比例尺( )。
A.成反比例 B.成正比例 C.不成比例
2、下列各题中,两种量成反比例关系是( )。
A 工作效率一定,工作时间和工作总量
B 一段路程一定,已走路程和剩下的路程
C 长方形周长一定,它的长和宽
D 平行四边形面积一定,它的底和高
3、表示a和b这两种量成反比例的关系式是( )
A.a+b=8 B.a-b=8 C.a×b=8 D.a÷b=8
4、被减数一定,减数与差( )
A.成正比例 B.成反比例 C.不成比例
5、花生的出油率一定,花生的重量和油的重量( )
A.成正比例 B.成反比例 C.不成比例
练习与提高:
根据关系式判断各题中两种量是不是成比例,成什么比例。
⑴收入一定,支出和节余。
⑵出米率一定,稻谷的重量和大米的重量。
⑶圆柱的侧面积一定,它的底面周长和高。
解比例
0.5:0.25=0.6:x
x: =12:
=7.5:x
4
3
8
1
0.04
2.5
×6
×6
√
√
√
×3
×3
1. 正比例和反比例的意义如何体现在习题中?
2.判断成正比例和反比例练习
关于正比例和反比例的应用你思考是什么?
五.探索与交流
梳理旧知,探寻联系
正比例和反比例
监控:说说你判断的理由。
预设:
正比例: 1、4。
反比例: 2、6。
不成比例:3、5。
预设:
①两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量
中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的
关系叫做正比例关系。
②两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量
中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的
关系叫做反比例关系。
判断:
1、甲、乙两数互为倒数,甲数和乙数成反比例。( )
2、一批货物,运走的和剩下的成反比例。 ( )
3、如果ab + 5 = 15,则a与b成反比例。( )
4、表示正比例关系的图像是一条直线。 ( )
5、一个人的身高与他的年龄成反比例。 ( )
课堂小结
比和比例
比
比例
比的基本性质,商不变的规律,分数的基本性质
求比值、化简比
用比的基本性质解决问题
正比例关系,反比例关系之间的联系与区别
解比例
用比例的基本性质解决问题
联系与区别
同学们再见
比和比例
﹙二﹚汇报交流
梳理旧知,探寻联系
1. 知识联系
预设②:
比例
比例应用
反比例意义
比和比例
比
求比值
比的性质
比的意义
化简比
比、分数和除法的关系
比的应用
a : b=
b
a
= a÷ b
比例的应用
按比分配
求比例尺
求图上距离
求实际距离
比例的意义
正比例意义
比例的基本性质
解比例
正比例意义
反比例意义
绿色圃中小学教育网http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育网http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
下面五个式子,哪几个是比,哪几个是比例?
(1)36:24
(2)2.4:1.6=60:40
(4)1.4:20=28:40
(3)5.2:0.13
(5)
5
8
:
3
2
(1)36:24
(3)5.2:0.13
(5)
5
8
:
3
2
(2)2.4:1.6=60:40
(4)1.4:20=28:40
判断比和比例
比
比例
比和比例的区别与联系
比 比例
意义
构成
基本性质
两个数相除又叫做两
个数的比。
表示两个比相等的式子
叫做比例。
0.9∶0.6 = 1.5
前项
后项
比值
5 ∶ 6 = 20∶24
内项
外项
比的前项和后项同时乘或除以相同的数(0除外),比值不变。应用比的基本性质可以把比化成最简单的整数比。
在比例里,两个内项的积等于两个外项的积。
应用比例的基本性质可以判断两个比能否组成比例。还可以解比例。
1.比和比例的区别?比和比值意义?
2.比和比例基本性质的区别?
3.比例基本性质的作用?比的基本性质的作用?
4.比各部分的名称?比例各部分的名称?
关于比和比例你想说什么?
一.探索与交流
正比例图
36:24
24:16
18:12
12:8
3:2
0
3
6
9
12
15
18
21
24
33
27
30
36
2
4
6
8
10
12
16
22
14
20
18
24
(3,2)
(12,8)
(18,12)
(24,16)
(36,24)
我会判
下面各题中的两个量是不是成比例?如果成比例,成什么比例?
1.全班人数一定,出勤人数和缺勤人数。( )
2.三角形的面积一定,它的底和高。( )
3.正方体一个面的面积和它的表面积。( )
4.圆的面积和半径。( )
不成比例
成反比例
成正比例
不成比例
1.什么是求比值?结果是什么形式的?
2.什么是化简比?结果又是什么形式的?
关于求比值和化简比你分得清楚吗?
三.探索与交流
小结:刚才同学们从知识内在联系和区别两方面梳理了比和比例的知识。
想必大家又有了新的收获。
提问4:比、比例的基本性质有什么用途呢?
预设:
①比的基本性质可以帮助我们把比化成最简单的整数比。
②比例的基本性质可以帮助我们解比例。
梳理旧知,探寻联系
汇报交流
出示练习:
化简比:
解比例:
3
2
2∶
7
2
4
1
∶x = ∶2
绿色圃中小学教育网http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
绿色圃中小学教育网http://www.Lspjy.com 绿色圃中学资源网http://cz.Lspjy.com
选择题。
1、实际距离一定,图上距离和比例尺( )。
A.成反比例 B.成正比例 C.不成比例
2、下列各题中,两种量成反比例关系是( )。
A 工作效率一定,工作时间和工作总量
B 一段路程一定,已走路程和剩下的路程
C 长方形周长一定,它的长和宽
D 平行四边形面积一定,它的底和高
3、表示a和b这两种量成反比例的关系式是( )
A.a+b=8 B.a-b=8 C.a×b=8 D.a÷b=8
4、被减数一定,减数与差( )
A.成正比例 B.成反比例 C.不成比例
5、花生的出油率一定,花生的重量和油的重量( )
A.成正比例 B.成反比例 C.不成比例
练习与提高:
根据关系式判断各题中两种量是不是成比例,成什么比例。
⑴收入一定,支出和节余。
⑵出米率一定,稻谷的重量和大米的重量。
⑶圆柱的侧面积一定,它的底面周长和高。
解比例
0.5:0.25=0.6:x
x: =12:
=7.5:x
4
3
8
1
0.04
2.5
×6
×6
√
√
√
×3
×3
1. 正比例和反比例的意义如何体现在习题中?
2.判断成正比例和反比例练习
关于正比例和反比例的应用你思考是什么?
五.探索与交流
梳理旧知,探寻联系
正比例和反比例
监控:说说你判断的理由。
预设:
正比例: 1、4。
反比例: 2、6。
不成比例:3、5。
预设:
①两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量
中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的
关系叫做正比例关系。
②两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量
中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的
关系叫做反比例关系。
判断:
1、甲、乙两数互为倒数,甲数和乙数成反比例。( )
2、一批货物,运走的和剩下的成反比例。 ( )
3、如果ab + 5 = 15,则a与b成反比例。( )
4、表示正比例关系的图像是一条直线。 ( )
5、一个人的身高与他的年龄成反比例。 ( )
课堂小结
比和比例
比
比例
比的基本性质,商不变的规律,分数的基本性质
求比值、化简比
用比的基本性质解决问题
正比例关系,反比例关系之间的联系与区别
解比例
用比例的基本性质解决问题
联系与区别
同学们再见
