人教版六年级下学期数学5数学广角-鸽巢问题课件(共20张PPT)
文档属性
| 名称 | 人教版六年级下学期数学5数学广角-鸽巢问题课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 10:22:17 | ||
图片预览








文档简介
(共20张PPT)
数学广角-鸽巢问题
学习目标:
1、我会用图示、分解数、假设等方法,理解并确认“抽屉原理”;
2、我能运用有余数除法解决抽屉问题。
新课讲解
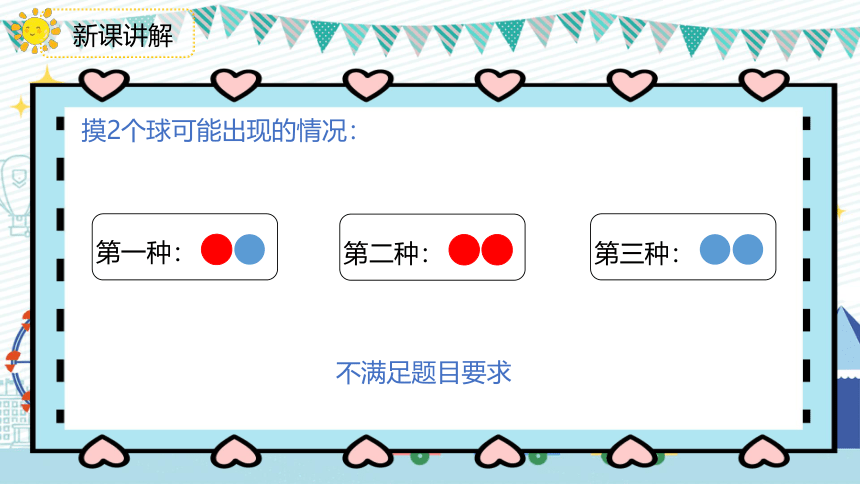
摸2个球可能出现的情况:
第一种:
第二种:
第三种:
不满足题目要求
方 法 一
运用知识 检测反馈
任务:书本第69页“做一做”
1、11只鸽子飞进了4个鸽笼,总有一个鸽笼里至少飞进了3只鸽子。为什么?
2、5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
要求:1.独立完成。
2.小组同学相互交流检查。
评价:回答完整,表达准确
巩固练习
摸出5个球肯定有两个球是同色的。因为……
有两种颜色。那摸3个球就能保证……
只摸2个球能保证是同色吗?
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球
运用知识 检测反馈
任务:书本第68页“做一做”
1、5只鸽子飞进了3个鸽笼,总有一个鸽笼里至少飞进了2只鸽子。为什么?
2、你理解上面扑克牌的道理了吗?
要求:1.独立完成。
2.小组同学相互交流检查。
巩固练习
评价:回答完整,表达准确
新课讲解
六年级里至少有两人的生日是同一天。
367÷366=1(人)……1(人)
1+1=2(人)
六年级里至少有两人的生日是同一天说法正确。
把一年366天看作366个抽屉。
假设每个笔筒里先放1支铅笔,最多放3支,剩下的1支无论放进哪个笔筒里,总有一个笔筒里至少放2支笔。
假设法说理
先把3支笔都放在一个笔筒里。
把此问题转化成抽屉问题。
b.解答:
根据抽屉原理,假设最少摸出m个球,则有
m÷2=1 …… n,当n=1时,m是最小的,此时m=3,即至少要摸出3个球,才能保证有2个球是同色的。
课堂练习
一只布袋中装有黑、白、红、蓝4种颜色的手套,问至少要摸出多少只手套才能保证有5副同颜色的?
四种不同的颜色看成是4个抽屉,每个抽屉都摸出9只手套,此时任意摸出1只,必定保证有一个抽屉有10只手套,即5副同颜色的手套。
9×4+1=37(只)
答:至少要摸出37只手套才能保证有5副同颜色的。
把 4 支笔放进 3 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 5 支笔放进 4 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 6 支笔放进 5 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 10 支笔放进 9 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
n+1
n
把n+1个物体放进n个抽屉里,不管怎么放,
总有一个抽屉里至少放进2个物体。
我的发现
随意找13位老师,他们中至少有几个人的属相相同?为什么?
13÷12=1
……
1
1+1 = 2
12个抽屉
12个属相
13个物体
13个人
解答鸽巢问题的关键是什么?
找准哪个是物体,也就是被装的;哪个是抽屉,也就是装东西的。以及他们的个数。
有余数时:
物体数÷抽屉数 = 商
……
余数
至少数 = 商 + 1
无余数时:
物体数÷抽屉数 = 商
至少数 = 商
把实际问题转化成“鸽巢问题”,弄清“鸽巢”和要被分放的“鸽子”。
物体数÷抽屉数=商……余数
至少数=商+1
“鸽巢问题”
的应用
1、课后练习:第1、2题;
2、练习册:《鸽巢问题(2)》
课后作业
聪明出于勤奋,天才在于积累。
数学广角-鸽巢问题
学习目标:
1、我会用图示、分解数、假设等方法,理解并确认“抽屉原理”;
2、我能运用有余数除法解决抽屉问题。
新课讲解
摸2个球可能出现的情况:
第一种:
第二种:
第三种:
不满足题目要求
方 法 一
运用知识 检测反馈
任务:书本第69页“做一做”
1、11只鸽子飞进了4个鸽笼,总有一个鸽笼里至少飞进了3只鸽子。为什么?
2、5个人坐4把椅子,总有一把椅子上至少坐2人。为什么?
要求:1.独立完成。
2.小组同学相互交流检查。
评价:回答完整,表达准确
巩固练习
摸出5个球肯定有两个球是同色的。因为……
有两种颜色。那摸3个球就能保证……
只摸2个球能保证是同色吗?
盒子里有同样大小的红球和蓝球各4个,要想摸出的球一定有2个同色的,至少要摸出几个球
运用知识 检测反馈
任务:书本第68页“做一做”
1、5只鸽子飞进了3个鸽笼,总有一个鸽笼里至少飞进了2只鸽子。为什么?
2、你理解上面扑克牌的道理了吗?
要求:1.独立完成。
2.小组同学相互交流检查。
巩固练习
评价:回答完整,表达准确
新课讲解
六年级里至少有两人的生日是同一天。
367÷366=1(人)……1(人)
1+1=2(人)
六年级里至少有两人的生日是同一天说法正确。
把一年366天看作366个抽屉。
假设每个笔筒里先放1支铅笔,最多放3支,剩下的1支无论放进哪个笔筒里,总有一个笔筒里至少放2支笔。
假设法说理
先把3支笔都放在一个笔筒里。
把此问题转化成抽屉问题。
b.解答:
根据抽屉原理,假设最少摸出m个球,则有
m÷2=1 …… n,当n=1时,m是最小的,此时m=3,即至少要摸出3个球,才能保证有2个球是同色的。
课堂练习
一只布袋中装有黑、白、红、蓝4种颜色的手套,问至少要摸出多少只手套才能保证有5副同颜色的?
四种不同的颜色看成是4个抽屉,每个抽屉都摸出9只手套,此时任意摸出1只,必定保证有一个抽屉有10只手套,即5副同颜色的手套。
9×4+1=37(只)
答:至少要摸出37只手套才能保证有5副同颜色的。
把 4 支笔放进 3 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 5 支笔放进 4 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 6 支笔放进 5 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
把 10 支笔放进 9 个笔筒里,不管怎么放,总有一个笔筒里至少放进 2 支笔。
n+1
n
把n+1个物体放进n个抽屉里,不管怎么放,
总有一个抽屉里至少放进2个物体。
我的发现
随意找13位老师,他们中至少有几个人的属相相同?为什么?
13÷12=1
……
1
1+1 = 2
12个抽屉
12个属相
13个物体
13个人
解答鸽巢问题的关键是什么?
找准哪个是物体,也就是被装的;哪个是抽屉,也就是装东西的。以及他们的个数。
有余数时:
物体数÷抽屉数 = 商
……
余数
至少数 = 商 + 1
无余数时:
物体数÷抽屉数 = 商
至少数 = 商
把实际问题转化成“鸽巢问题”,弄清“鸽巢”和要被分放的“鸽子”。
物体数÷抽屉数=商……余数
至少数=商+1
“鸽巢问题”
的应用
1、课后练习:第1、2题;
2、练习册:《鸽巢问题(2)》
课后作业
聪明出于勤奋,天才在于积累。
