9.2.4总体离散程度的估计 课件(共30张PPT)
文档属性
| 名称 | 9.2.4总体离散程度的估计 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 10:08:29 | ||
图片预览











文档简介
(共30张PPT)
9.2.4 总体离散程度的估计
学习目标
阅读教材209-213页,回答下列问题:
问题1:描述数据离散程度的统计量有哪些
问题2:标准差的意义是什么
一、创设情境,新知导入
甲、乙两名战士在相同条件下各射靶10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7;
乙:6,7,7,8,6,7,8,7,9,5.
经过计算可知甲、乙的命中环数的平均数都是7环.
【问题】观察上述两组数据,如果你是教练,你认为选哪个人比较合适
右图是命中环数与次数的柱状图,你能从中发现什么?
思考:
当样本的众数、中位数、平均数,极差不足以准确描述总体分布情况时,我们应该引进哪种概念来估计总体分布?
即怎么描述数据的“稳不稳定”、“集中”、和离散程度?
二、数学建模、直观感受,形成概念
X=182cm
这一组数据的波动怎么去描述?
平均距离:用各数与均值的"距离"的差的绝对值
需要求“平均距离”
1.“平均距离”—平均差:
2.方差:样本各数据到平均数的距离的平方的平均值
3.标准差:方差的算术平方根 S
三 、概念形成,初探新知
注意:是不是标准差或方差低,该组数据就是最优选,最好的?
知识点四 标准差的意义
标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.
注意:考虑均值,反应真实的水平,再去考虑数据的稳定性!!
知识点五 分层随机抽样的方差
四、例题示范,巩固新知
1、甲乙两台机床同时生产一种零件,10天中两台机床每天出的次品数为:
甲 0 1 0 2 2 0 3 1 2 4
乙 2 3 1 1 0 2 1 1 0 1
分别计算这两组数据的平均数与标准差,从计算结果来看,哪台机床的性能好?
四、例题示范,巩固新知
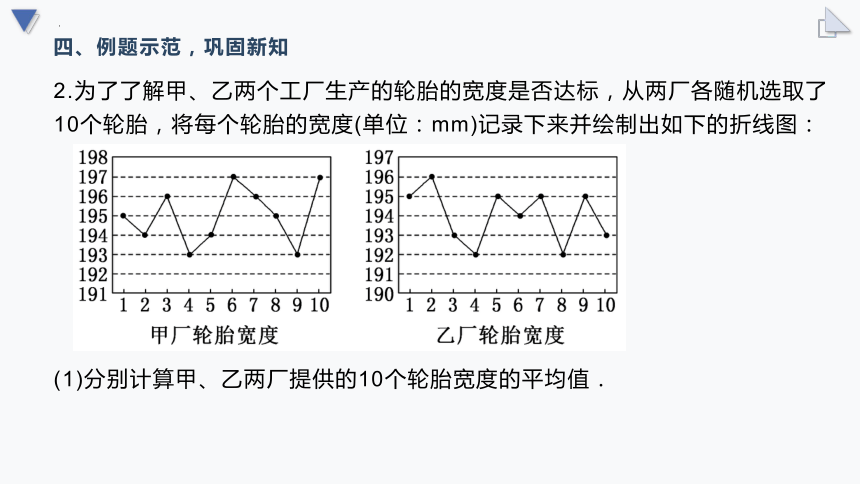
2.为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,从两厂各随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下的折线图:
(1)分别计算甲、乙两厂提供的10个轮胎宽度的平均值.
为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,从两厂各随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下的折线图:
(2)若轮胎的宽度在[194,196]内,则称这个轮胎是标准轮胎.试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个的轮胎相对更好.
【做一做】
某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4
则(1)平均命中环数为________;
(2)命中环数的标准差为________.
五、课堂练习
1.方差、标准差的计算
例1.甲、乙两机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
2.分层随机抽样的方差
例2.甲、乙两支田径队的体检结果为:甲队体重的平均数为60 kg,方差为200,乙队体重的平均数为70 kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,那么甲、乙两队全部队员的平均体重和方差分别是多少?
2.分层随机抽样的方差
例2.甲、乙两支田径队的体检结果为:甲队体重的平均数为60 kg,方差为200,乙队体重的平均数为70 kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,那么甲、乙两队全部队员的平均体重和方差分别是多少?
【巩固练习2】
某学校统计教师职称及年龄,中级职称教师的人数为50人,其平均年龄为38岁,方差是2,高级职称的教师3人58岁,5人40岁,2人38岁,求该校中级职称和高级职称教师年龄的平均数和方差.
课堂小结
谢谢观看
9.2.4 总体离散程度的估计
学习目标
阅读教材209-213页,回答下列问题:
问题1:描述数据离散程度的统计量有哪些
问题2:标准差的意义是什么
一、创设情境,新知导入
甲、乙两名战士在相同条件下各射靶10次,每次命中的环数分别是:
甲:8,6,7,8,6,5,9,10,4,7;
乙:6,7,7,8,6,7,8,7,9,5.
经过计算可知甲、乙的命中环数的平均数都是7环.
【问题】观察上述两组数据,如果你是教练,你认为选哪个人比较合适
右图是命中环数与次数的柱状图,你能从中发现什么?
思考:
当样本的众数、中位数、平均数,极差不足以准确描述总体分布情况时,我们应该引进哪种概念来估计总体分布?
即怎么描述数据的“稳不稳定”、“集中”、和离散程度?
二、数学建模、直观感受,形成概念
X=182cm
这一组数据的波动怎么去描述?
平均距离:用各数与均值的"距离"的差的绝对值
需要求“平均距离”
1.“平均距离”—平均差:
2.方差:样本各数据到平均数的距离的平方的平均值
3.标准差:方差的算术平方根 S
三 、概念形成,初探新知
注意:是不是标准差或方差低,该组数据就是最优选,最好的?
知识点四 标准差的意义
标准差刻画了数据的离散程度或波动幅度,标准差越大,数据的离散程度越大;标准差越小,数据的离散程度越小.
注意:考虑均值,反应真实的水平,再去考虑数据的稳定性!!
知识点五 分层随机抽样的方差
四、例题示范,巩固新知
1、甲乙两台机床同时生产一种零件,10天中两台机床每天出的次品数为:
甲 0 1 0 2 2 0 3 1 2 4
乙 2 3 1 1 0 2 1 1 0 1
分别计算这两组数据的平均数与标准差,从计算结果来看,哪台机床的性能好?
四、例题示范,巩固新知
2.为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,从两厂各随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下的折线图:
(1)分别计算甲、乙两厂提供的10个轮胎宽度的平均值.
为了了解甲、乙两个工厂生产的轮胎的宽度是否达标,从两厂各随机选取了10个轮胎,将每个轮胎的宽度(单位:mm)记录下来并绘制出如下的折线图:
(2)若轮胎的宽度在[194,196]内,则称这个轮胎是标准轮胎.试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小,根据两厂的标准轮胎宽度的平均水平及其波动情况,判断这两个工厂哪个的轮胎相对更好.
【做一做】
某学员在一次射击测试中射靶10次,命中环数如下:7,8,7,9,5,4,9,10,7,4
则(1)平均命中环数为________;
(2)命中环数的标准差为________.
五、课堂练习
1.方差、标准差的计算
例1.甲、乙两机床同时加工直径为100 cm的零件,为检验质量,各从中抽取6件测量,数据为
甲:99 100 98 100 100 103
乙:99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工零件的质量更稳定.
2.分层随机抽样的方差
例2.甲、乙两支田径队的体检结果为:甲队体重的平均数为60 kg,方差为200,乙队体重的平均数为70 kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,那么甲、乙两队全部队员的平均体重和方差分别是多少?
2.分层随机抽样的方差
例2.甲、乙两支田径队的体检结果为:甲队体重的平均数为60 kg,方差为200,乙队体重的平均数为70 kg,方差为300,又已知甲、乙两队的队员人数之比为1∶4,那么甲、乙两队全部队员的平均体重和方差分别是多少?
【巩固练习2】
某学校统计教师职称及年龄,中级职称教师的人数为50人,其平均年龄为38岁,方差是2,高级职称的教师3人58岁,5人40岁,2人38岁,求该校中级职称和高级职称教师年龄的平均数和方差.
课堂小结
谢谢观看
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
