华东师大版数学八年级下册第19章 矩形、菱形与正方形定向训练试题(含解析)
文档属性
| 名称 | 华东师大版数学八年级下册第19章 矩形、菱形与正方形定向训练试题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 606.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 00:00:00 | ||
图片预览



文档简介
华东师大版数学八年级下册第19章 矩形、菱形与正方形定向训练
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列命题中,是真命题的是( ).A.三角形的外心是三角形三个内角角平分线的交点
B.满足的三个数,,是勾股数
C.对角线相等的四边形各边中点连线所得四边形是矩形
D.五边形的内角和为
2、在数学活动课上,老师和同学们判断一个四边形门框是否为矩形.下面是某个合作小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量其内角是否均为直角 D.测量对角线是否垂直
3、如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=AD,则∠ACE的度数为( )
A.22.5° B.27.5° C.30° D.35°
4、如图,已知E为邻边相等的平行四边形ABCD的边BC上一点,且∠DAE=∠B=80 ,那么∠CDE的度数为( )
A.20 B.25 C.30 D.35
5、如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.DE⊥DC C.∠ADB=90° D.CE⊥DE
6、如图,正方形OABC的边长为4,点D是OA边的中点,连接CD,将△OCD沿着CD折叠得到△ECD,CE与OB交于点F.若反比例函数y=的图象经过点F,则m的值为( )
A. B. C. D.
7、菱形ABCD的周长是8cm,∠ABC=60°,那么这个菱形的对角线BD的长是( )
A.cm B.2cm C.1cm D.2cm
8、如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记的面积为,的面积为,若正方形的边长,,则的大小为( )
A.6 B.7 C.8 D.9
9、下列命题是真命题的是( )
A.五边形的内角和是720° B.三角形的任意两边之和大于第三边
C.内错角相等 D.对角线互相垂直的四边形是菱形
10、下列命题正确的是( )
A.若,则 B.四条边相等的四边形是正四边形
C.有一组邻边相等的平行四边形是矩形 D.如果,则
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题6分,共计30分)
1、如图,在正方形ABCD中,,M是AD边上的一点,.将△BMA沿BM对折至△BMN,连接DN,则DN的长是________.
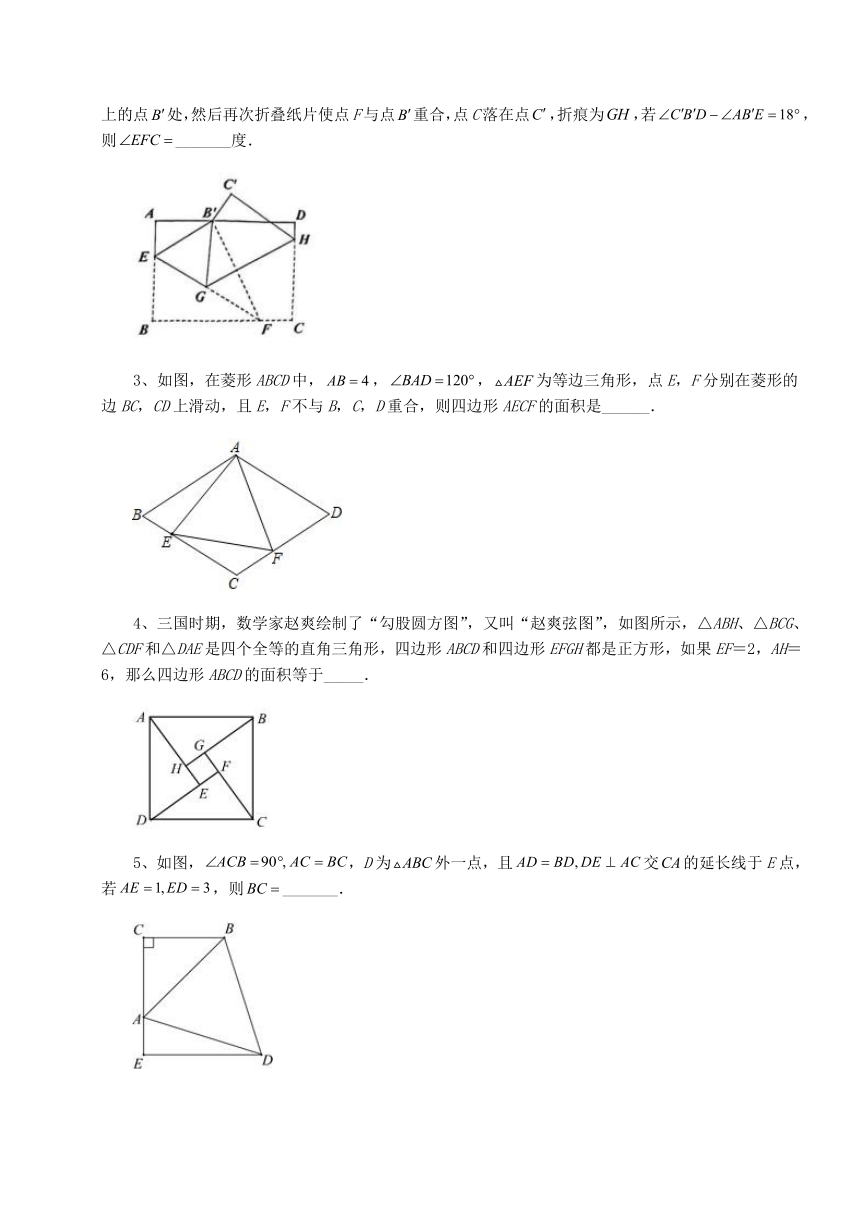
2、如图,长方形纸片,点E,F分别在边上,将纸片沿折叠,使点B落在边上的点处,然后再次折叠纸片使点F与点重合,点C落在点,折痕为,若,则_______度.
3、如图,在菱形ABCD中,,,为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合,则四边形AECF的面积是______.
4、三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形,如果EF=2,AH=6,那么四边形ABCD的面积等于_____.
5、如图,,D为外一点,且交的延长线于E点,若,则_______.
三、解答题(4小题,每小题10分,共计40分)
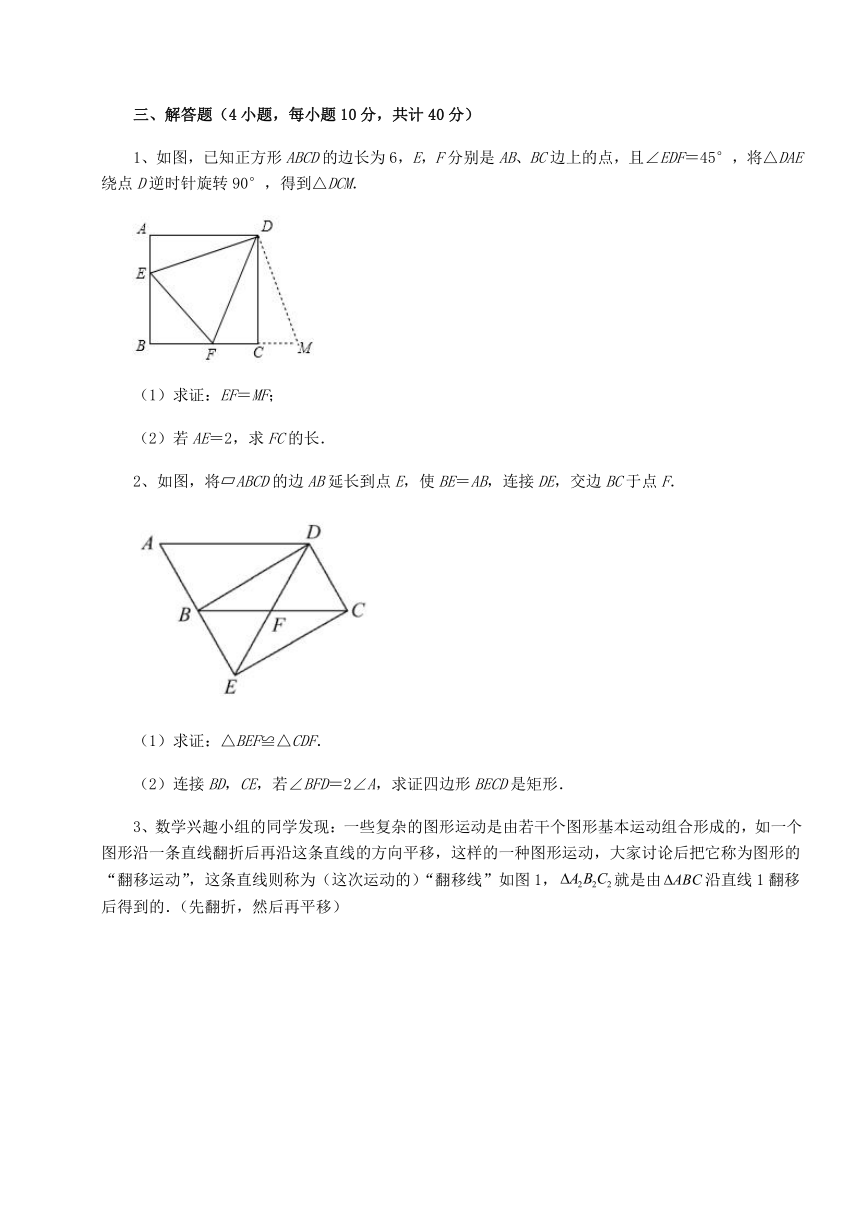
1、如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=MF;
(2)若AE=2,求FC的长.
2、如图,将 ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
3、数学兴趣小组的同学发现:一些复杂的图形运动是由若干个图形基本运动组合形成的,如一个图形沿一条直线翻折后再沿这条直线的方向平移,这样的一种图形运动,大家讨论后把它称为图形的“翻移运动”,这条直线则称为(这次运动的)“翻移线”如图1,就是由沿直线1翻移后得到的.(先翻折,然后再平移)
(1)在学习中,兴趣小组的同学就“翻移运动”对应点(指图1中的与,与…)连线是否被翻移线平分发生了争议.对此你认为如何?(直接写出你的判断)
(2)如图2,在长方形中,,点分别是边中点,点在边延长线上,联结,如果是经过“翻移运动”得到的三角形.请在图中画出上述“翻移运动”的“翻移线”直线;联结,线段和直线交于点,若的面积为3,求此长方形的边长的长.
(3)如图3,是(2)中的长方形边上一点,如果,先按(2)的“翻移线”直线翻折,然后再平移2个单位,得到,联结线段,分别和“翻移线”交于点和点,求四边形的面积.
4、如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连结AG、DE.
(1)猜想AG与DE的数量关系,请直接写出结论;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转,旋转角为α(0°<α<180°),得到图2,请判断:
(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)在正方形OEFG旋转过程中,请直接写出:
①当α=30°时,∠OAG的度数;
②当△AEG的面积最小时,旋转角α的度数.
-参考答案-
一、单选题
1、D
【解析】
【分析】
正确的命题是真命题,根据定义解答.
【详解】
解:A. 三角形的外心是三角形三条边垂直平分线的交点,故该项不符合题意;
B. 满足的三个正整数,,是勾股数,故该项不符合题意;
C. 对角线相等的四边形各边中点连线所得四边形是菱形,故该项不符合题意;
D. 五边形的内角和为,故该项符合题意;
故选:D.
【点睛】
此题考查了真命题的定义,正确掌握三角形外心的定义,勾股数的定义,中点四边形的判定定理及多边形内角和的计算公式是解题的关键.
2、C
【解析】
【分析】
根据矩形的判定:(1)四个角均为直角;(2)对边互相平行且相等;(3)对角线相等且平分,据此即可判断结果.
【详解】
解:A、根据矩形的对角线相等且平分,故错误;
B、对边分别相等只能判定四边形是平行四边形,故错误;
C、矩形的四个角都是直角,故正确;
D、矩形的对角线互相相等且平分,所以垂直与否与矩形的判定无关,故错误.
故选:C.
【点睛】
本题主要考查的是矩形的判定方法,熟练掌握矩形的判定是解题的关键.
3、A
【解析】
【分析】
利用正方形的性质证明∠DBC=45°和BE=BC,进而证明∠BEC=67.5°.
【详解】
解:∵四边形ABCD是正方形,
∴BC=AD,∠DBC=45°,
∵BE=AD,
∴BE=BC,
∴∠BEC=∠BCE=(180°﹣45°)÷2=67.5°,
∵AC⊥BD,
∴∠COE=90°,
∴∠ACE=90°﹣∠BEC=90°﹣67.5°=22.5°,
故选:A.
【点睛】
本题考查正方形的性质,以及等腰三角形的性质,掌握正方形的性质并加以利用是解决本题的关键.
4、C
【解析】
【分析】
依题意得出AE=AB=AD,∠ADE=50°,又因为∠B=80°故可推出∠ADC=80°,∠CDE=∠ADC-∠ADE,从而求解.
【详解】
∵ADBC,
∴∠AEB=∠DAE=∠B=80°,
∴AE=AB=AD,
在三角形AED中,AE=AD,∠DAE=80°,
∴∠ADE=50°,
又∵∠B=80°,
∴∠ADC=80°,
∴∠CDE=∠ADC-∠ADE=30°.
故选:C.
【点睛】
考查菱形的边的性质,同时综合利用三角形的内角和及等腰三角形的性质,解题关键是利用等腰三角形的性质求得∠ADE的度数.
5、B
【解析】
【分析】
先证明四边形BCED为平行四边形,再根据矩形的判定进行解答.
【详解】
解:∵四边形ABCD为平行四边形,
∴AD∥BC,且AD=BC,
又∵AD=DE,
∴DE∥BC,且DE=BC,
∴四边形BCED为平行四边形,
A、∵AB=BE,DE=AD,
∴BD⊥AE,
∴□DBCE为矩形,故本选项不符合题意;
B、∵DE⊥DC,
∴∠EDB=90°+∠CDB>90°,
∴四边形DBCE不能为矩形,故本选项符合题意;
C、∵∠ADB=90°,
∴∠EDB=90°,
∴□DBCE为矩形,故本选项不符合题意;
D、∵CE⊥DE,
∴∠CED=90°,
∴□DBCE为矩形,故本选项不符合题意.
故选:B.
【点睛】
本题考查了平行四边形的判定和性质、矩形的判定等知识,判定四边形BCED为平行四边形是解题的关键.
6、B
【解析】
【分析】
先根据折叠的性质得到,,设,利用两点间的距离公式得到,,解关于、的方程组得到点的坐标为,,再利用待定系数法求出直线的解析式为,易得直线的解析式为,解方程组得,,然后根据反比例函数图象上点的坐标特征求的值.
【详解】
解:正方形的边长为4,点是边的中点,
,,,,
沿着折叠得到,
,,
设,
,
,
,,
点的坐标为,,
设直线的解析式为,
把,,分别代入得,
解得,
直线的解析式为,
易得直线的解析式为,
解方程组得,
,,
点,在反比例函数的图象上,
.
故选:B.
【点睛】
本题考查了反比例函数图象上点的坐标特征,解题的关键是掌握反比例函数为常数,的图象是双曲线,图象上的点的横纵坐标的积是定值,即.也考查了正方形的性质和折叠的性质.
7、B
【解析】
【分析】
由菱形的性质得AB=BC=2(cm),OA=OC,OB=OD,AC⊥BD,再证△ABC是等边三角形,得AC=AB=2(cm),则OA=1(cm),然后由勾股定理求出OB=(cm),即可求解.
【详解】
解:∵菱形ABCD的周长为8cm,
∴AB=BC=2(cm),OA=OC,OB=OD,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2cm,
∴OA=1(cm),
在Rt△AOB中,由勾股定理得:OB===(cm),
∴BD=2OB=2(cm),
故选:B.
【点睛】
此题考查了菱形的性质,勾股定理,等边三角形的性质和判定,解题的关键是熟练掌握菱形的性质,勾股定理,等边三角形的性质和判定方法.
8、D
【解析】
【分析】
由题意依据全等三角形的判定得出△BOM≌△CON,进而根据正方形的性质即可得出的大小.
【详解】
解:∵正方形ABCD的对角线AC,BD交于点O,
∴OC=OD=BO=AO,∠ABO=∠ACB=45°,AC⊥BD.
∵∠MOB+∠BON=90°,∠BON+∠CON=90°
∴∠BOM=∠CON,且OC=OB,∠ABO=∠ACB=45°,
∴△BOM≌△CON(ASA),=S△BOM,
∴,
∵=S正方形ABCD,正方形的边长,,
∴=S正方形ABCD -=.
故选:D.
【点睛】
本题考查正方形的性质以及全等三角形的判定和性质等知识,灵活运用这些性质进行推理是解答本题的关键.
9、B
【解析】
【分析】
利用多边形的内角和公式、三角形的三边关系、平行线的性质及菱形的判定分别判断后即可确定正确的选项.
【详解】
解:A、五边形的内角和为540°,故原命题错误,是假命题,不符合题意;
B、三角形的任意两边之和大于第三边,正确,是真命题,符合题意;
C、两直线平行,内错角相等,故原命题错误,是假命题,不符合题意;
D、对角线互相垂直的平行四边形是菱形,故原命题错误,是假命题,不符合题意,
故选:B.
【点睛】
本题考查了命题与定理的知识,解题的关键是了解多边形的内角和公式、三角形的三边关系、平行线的性质及菱形的判定等知识,难度不大.
10、A
【解析】
【分析】
利用等式的性质以及矩形、正方形、菱形的判定方法分别判断后即可确定正确的选项.
【详解】
解:A、若,则,故此命题正确;
B、四条边相等的四边形是菱形,故原命题不正确;
C、有一组邻边相等的平行四边形是菱形,故原命题不正确;
D、如果,a≠0时,则,若时,此命题不正确,
故选:A.
【点睛】
本题考查了命题与定理以及等式的性质等知识,解题的关键是了解矩形及菱形的判定方法.
二、填空题
1、
【解析】
【分析】
连接AN交BM于点O,过点N作NH⊥AD于点H,根据正方形的性质可得AM=3,DM=6,从而得到,再由轴对称图形的性质,可得AN⊥BM,AO=NO,MN=AM=3,再由,可得,从而得到,再由勾股定理可得,从而得到,进而得到, ,即可求证.
【详解】
解:如图,连接AN交BM于点O,过点N作NH⊥AD于点H,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵, .
∴AM=3,DM=6,
∴ ,
∵将△BMA沿BM对折至△BMN,
∴AN⊥BM,AO=NO,MN=AM=3,
∵ ,
∴ ,
∴,
在 中,由勾股定理得:
,
在 中,由勾股定理得:
,
∴,
即 ,解得: ,
∴ , ,
∴ ,
∴ .
故答案为:
【点睛】
本题主要考查了正方形与折叠问题,勾股定理,轴对称图形的性质,熟练掌握相关知识点是解题的关键.
2、144
【解析】
【分析】
根据将纸片沿折叠,使点B落在边上的点处,得出∠EB′F=∠B=90°,∠BFE=∠B′FE,可得∠AB′E+∠DB′F=90°根据四边形ABCD为矩形,得出AD∥BC,可得∠DBF=∠B′FB=2∠EFB,可求∠AB′E =90°-∠DB′F=90°-2∠EFB,根据GH为对称轴,可得∠CB′F=∠CFB′=180°-∠B′FB=180°-2∠EFB,可得∠C′B′D=∠C′B′F-∠FB′D=180°-2∠EFB-2∠EFB,根据,列方程180°-2∠EFB-2∠EFB-(90°-2∠EFB)=18°,解方程即可.
【详解】
解:∵将纸片沿折叠,使点B落在边上的点处,
∴∠EB′F=∠B=90°,∠BFE=∠B′FE,
∴∠AB′E+∠DB′F=90°
∴∠AB′E =90°-∠DB′F
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DB′F=∠B′FB=2∠EFB,
∴∠AB′E =90°-∠DBF=90°-2∠EFB,
∵GH为对称轴,
∴∠C′B′F=∠CFB′=180°-∠B′FB=180°-2∠EFB,
∵∠C′B′D=∠C′B′F-∠FB′D=180°-2∠EFB-2∠EFB,
∵,
∴180°-2∠EFB-2∠EFB-(90°-2∠EFB)=18°,
解得∠EFB=36°,
∴∠EFC=180°-∠EFB=180°-36°=144°.
故答案为144.
【点睛】
本题考查折叠性质,矩形性质,平行线性质,补角性质,列一元一次方程,掌握折叠性质,矩形性质,平行线性质,补角性质,列一元一次方程是解题关键.
3、
【解析】
【分析】
连接AC,根据菱形的性质及等边三角形的性质证明△ABE≌△ACF(ASA),得到S△ABE=S△ACF,进而得到四边形AECF的面积=S△ABC,过点A作AH⊥BC于H,由勾股定理求出AH,再利用三角形面积公式计算即可.
【详解】
解:连接AC,
∵四边形ABCD为菱形,∠BAD=120°,
∴∠1+∠EAC=60°,
∵为等边三角形,
∴∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC和△ACD为等边三角形,
∴∠4=60°,AC=AB,
∴△ABE≌△ACF(ASA),
∴S△ABE=S△ACF,
∴四边形AECF的面积=S△ABC,
过点A作AH⊥BC于H,则∠BAH=30°,
∴,
∴,
∴四边形AECF的面积=S△ABC=,
故答案为:.
【点睛】
此题考查了菱形的性质,等边三角形的性质,勾股定理,全等三角形的判定及性质,熟记菱形的性质及全等三角形的判定是解题的关键.
4、
【解析】
【分析】
由图知,四边形ABCD的面积=4个直角三角形面积的和+正方形EFGH的面积,由题意可求得直角三角形的面积及正方形EFGH的面积,从而可求得结果.
【详解】
∵四边形EFGH是正方形
∴GH=EF=2
∵△ABH≌△BCG
∴BG=AH=6
∴BH=BG+GH=6+2=8
∴
∵ △ABH、△BCG、△CDF和△DAE是四个全等的直角三角形
∴这四个直角三角形的面积均为24
∵四边形EFGH是正方形
∴
∴
故答案为:100
【点睛】
本题考查了正方形的性质、全等三角形的性质及图形的面积,关键是全等三角形的性质求得直角三角形的面积.
5、2
【解析】
【分析】
过点D作DM⊥CB于M,证出∠DAE=∠DBM,判定△ADE≌△BDM,得到DM=DE=3,证明四边形CEDM是矩形,得到CE=DM=3,由AE=1,求出BC=AC=2.
【详解】
解:∵DE⊥AC,
∴∠E=∠C=90°,
∴,
过点D作DM⊥CB于M,则∠M=90°=∠E,
∵AD=BD,
∴∠BAD=∠ABD,
∵AC=BC,
∴∠CAB=∠CBA,
∴∠DAE=∠DBM,
∴△ADE≌△BDM,
∴DM=DE=3,
∵∠E=∠C=∠M =90°,
∴四边形CEDM是矩形,
∴CE=DM=3,
∵AE=1,
∴BC=AC=2,
故答案为:2.
【点睛】
此题考查了全等三角形的判定及性质,矩形的判定及性质,等边对等角证明角度相等,正确引出辅助线证明△ADE≌△BDM是解题的关键.
三、解答题
1、(1)见解析;(2)FC=3.
【解析】
【分析】
(1)由旋转可得DE=DM,∠EDM为直角,可得出∠EDF+∠MDF=90°,由∠EDF=45°,得到∠MDF为45°,可得出∠EDF=∠MDF,再由DF=DF,利用SAS可得出三角形DEF与三角形MDF全等,由全等三角形的对应边相等可得出EF=MF;
(2)由(1)的全等得到AE=CM=2,正方形的边长为6,用AB﹣AE求出EB的长,再由BC+CM求出BM的长,设EF=MF=x,可得出BF=BM﹣FM=BM﹣EF=8﹣x,在直角三角形BEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为EF的长,由此即可求出CF的长.
【详解】
解:(1)∵四边形ABCD是正方形,
∴∠A=∠FCD=∠ADC=90°,
∵△DAE逆时针旋转90°得到△DCM,
∴∠A=∠DCM=90°,AE=CM,∠ADE=∠CDM,DE=DM
∴∠FCD+∠DCM=180°,∠ADE+∠EDC=∠CDM+∠EDC=90°,
∴F、C、M三点共线,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF;
(2)设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得,
即,
解得:x=5,
∴EF=5,
∴CF=FM-CM=EF-CM=3.
【点睛】
本题主要考查正方形的性质、旋转的性质、三角形全等及勾股定理,关键是根据半角旋转得到三角形的全等,然后利用勾股定理求得线段的长.
2、(1)见解析;(2)见解析
【解析】
【分析】
(1)根据平行四边形的性质可得ABCD且AB=CD,进而证明∠BEF=∠FDC,∠FBE=∠FCD, ASA证明△BEF≌△CDF.
(2)根据等边对等角证明FD=FC,进而证明,根据对角线相等的平行四边形是矩形即可证明
【详解】
(1)∵四边形ABCD为平行四边形,
∴ABCD且AB=CD.
∵BE=AB,
∴BECD且BE=CD.
∴∠BEF=∠FDC,∠FBE=∠FCD,
∴△BEF≌△CDF.
(2)∵BECD且BE=CD.
∴四边形BECD为平行四边形,
∴DF=DE,CF=BC,
∵四边形ABCD为平行四边形,
∴∠FCD=∠A,
∵∠BFD=∠FCD+∠FDC,∠BFD=2∠A,
∴∠FDC=∠FCD,
∴FD=FC.
又DF=DE,CF=BC,
∴BC=DE,
∴ BECD是矩形.
【点睛】
本题考查了平行四边形的性质与判定,矩形的判定,三角形全等的性质与判定,掌握平行四边形的性质与判定是解题的关键.
3、 (1)“翻移运动”对应点(指图1中的与,与连线被翻移线平分
(2)3
(3)11或10
【解析】
【分析】
(1)画出图形,即可得出结论;
(2)作直线,即为“翻移线”直线,再由“翻移运动”的性质和三角形面积关系求解即可;
(3)分两种情况:①先按(2)的“翻移线”直线翻折,然后再向上平移2个单位,②先按(2)的“翻移线”直线翻折,然后再向下平移2个单位,由“翻移运动”的性质、梯形面积公式和三角形面积公式分别求解即可.
(1)
解:如图1,连接,,
则“翻移运动”对应点(指图1中的与,与连线被翻移线平分;
(2)
解:作直线,即为“翻移线”直线,如图2所示:
四边形是长方形,
,,
由“翻移运动”的性质得:,,是的中点,
,
,
,
,
,
,
;
(3)
解:分两种情况:
①先按(2)的“翻移线”直线翻折,然后再向上平移2个单位,如图3所示:
设翻折后的三角形为,连接,
则,
同(2)得:,,
,,
,
四边形的面积梯形的面积的面积的面积;
②先按(2)的“翻移线”直线翻折,然后再向下平移2个单位,如图4所示:
设翻折后的三角形为,连接,
则,
同(2)得:,,
,,
,
四边形的面积梯形的面积的面积的面积;
综上所述,四边形的面积为11或10.
【点睛】
本题是四边形综合题目,考查了长方形的性质、“翻移运动”的性质、梯形面积公式、三角形面积公式等知识,本题综合性强,解题的关键是熟练掌握“翻移运动”的性质和长方形的性质.
4、(1)AG=DE;(2)成立,理由见解析;(3)①90°,②135°
【解析】
【分析】
(1)证明△AOG≌△DOE(SAS),得出AG=DE即可;
(2)先证明∠AOG=∠DOE,再证明△AOG≌△DOE(SAS),得出AG=DE即可;
(3)①过点E作EM⊥AC交AC的延长线于点M,证明△AOG≌△DOE,则可得出答案;
②作AH⊥GE于H,连接OH,则当O、A、H在同一直线上时OH最小,然后根据旋转的性质可得出答案.
【详解】
(1)证明:∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∴∠AOG=∠DOE=90°,
∵四边形OEFG是正方形,
∴OG=OE,
在△AOG和△DOE中
,
∴△AOG≌△DOE(SAS),
∴AG=DE;
(2)成立,理由:
∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∴∠AOD=∠DOC=90°,
∵∠DOG=∠COE=α,
∴∠AOG=∠DOE,
∵四边形OEFG是正方形,
∴OG=OE,
在△AOG和△DOE中
,
∴△AOG≌△DOE(SAS),
∴AG=DE;
(3)①过点E作EM⊥AC交AC的延长线于点M,则∠EMO=90°,
由旋转的性质可知∠MOE=∠DOG=α=30°,
∴∠MOE=90°-30°=60°,
∵点O是正方形ABCD两对角线的交点,
∴OA⊥OD,
∴∠AOG=90°-30°=60°,
∴∠AOG =∠MOE,
在△AOG和△DOE中
,
∴△AOG≌△DOE(SAS),
∴∠OAG=∠EMO=90°;
②作AH⊥GE于H,连接OH,
∵OG=2OD,OE=2OC,
∴OG、OE为定值,
∴GE=是定值,
∴当AH最小时,△AEG的面积最小,
∵当O、A、H在同一直线上时OH最小,OA为定值,
∴此时AH最小,即△AEG的面积最小,
此时的旋转角α=∠HOG+∠AOD=45°+90°=135°.
【点睛】
本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,旋转的性质等知识,熟练掌握旋转的性质及证明三角形全等是解决问题的关键.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、下列命题中,是真命题的是( ).A.三角形的外心是三角形三个内角角平分线的交点
B.满足的三个数,,是勾股数
C.对角线相等的四边形各边中点连线所得四边形是矩形
D.五边形的内角和为
2、在数学活动课上,老师和同学们判断一个四边形门框是否为矩形.下面是某个合作小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量其内角是否均为直角 D.测量对角线是否垂直
3、如图,正方形ABCD的两条对角线AC,BD相交于点O,点E在BD上,且BE=AD,则∠ACE的度数为( )
A.22.5° B.27.5° C.30° D.35°
4、如图,已知E为邻边相等的平行四边形ABCD的边BC上一点,且∠DAE=∠B=80 ,那么∠CDE的度数为( )
A.20 B.25 C.30 D.35
5、如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A.AB=BE B.DE⊥DC C.∠ADB=90° D.CE⊥DE
6、如图,正方形OABC的边长为4,点D是OA边的中点,连接CD,将△OCD沿着CD折叠得到△ECD,CE与OB交于点F.若反比例函数y=的图象经过点F,则m的值为( )
A. B. C. D.
7、菱形ABCD的周长是8cm,∠ABC=60°,那么这个菱形的对角线BD的长是( )
A.cm B.2cm C.1cm D.2cm
8、如图,正方形ABCD的对角线相交于点O,以点O为顶点的正方形OEGF的两边OE,OF分别交正方形ABCD的两边AB,BC于点M,N,记的面积为,的面积为,若正方形的边长,,则的大小为( )
A.6 B.7 C.8 D.9
9、下列命题是真命题的是( )
A.五边形的内角和是720° B.三角形的任意两边之和大于第三边
C.内错角相等 D.对角线互相垂直的四边形是菱形
10、下列命题正确的是( )
A.若,则 B.四条边相等的四边形是正四边形
C.有一组邻边相等的平行四边形是矩形 D.如果,则
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题6分,共计30分)
1、如图,在正方形ABCD中,,M是AD边上的一点,.将△BMA沿BM对折至△BMN,连接DN,则DN的长是________.
2、如图,长方形纸片,点E,F分别在边上,将纸片沿折叠,使点B落在边上的点处,然后再次折叠纸片使点F与点重合,点C落在点,折痕为,若,则_______度.
3、如图,在菱形ABCD中,,,为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合,则四边形AECF的面积是______.
4、三国时期,数学家赵爽绘制了“勾股圆方图”,又叫“赵爽弦图”,如图所示,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和四边形EFGH都是正方形,如果EF=2,AH=6,那么四边形ABCD的面积等于_____.
5、如图,,D为外一点,且交的延长线于E点,若,则_______.
三、解答题(4小题,每小题10分,共计40分)
1、如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=MF;
(2)若AE=2,求FC的长.
2、如图,将 ABCD的边AB延长到点E,使BE=AB,连接DE,交边BC于点F.
(1)求证:△BEF≌△CDF.
(2)连接BD,CE,若∠BFD=2∠A,求证四边形BECD是矩形.
3、数学兴趣小组的同学发现:一些复杂的图形运动是由若干个图形基本运动组合形成的,如一个图形沿一条直线翻折后再沿这条直线的方向平移,这样的一种图形运动,大家讨论后把它称为图形的“翻移运动”,这条直线则称为(这次运动的)“翻移线”如图1,就是由沿直线1翻移后得到的.(先翻折,然后再平移)
(1)在学习中,兴趣小组的同学就“翻移运动”对应点(指图1中的与,与…)连线是否被翻移线平分发生了争议.对此你认为如何?(直接写出你的判断)
(2)如图2,在长方形中,,点分别是边中点,点在边延长线上,联结,如果是经过“翻移运动”得到的三角形.请在图中画出上述“翻移运动”的“翻移线”直线;联结,线段和直线交于点,若的面积为3,求此长方形的边长的长.
(3)如图3,是(2)中的长方形边上一点,如果,先按(2)的“翻移线”直线翻折,然后再平移2个单位,得到,联结线段,分别和“翻移线”交于点和点,求四边形的面积.
4、如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连结AG、DE.
(1)猜想AG与DE的数量关系,请直接写出结论;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转,旋转角为α(0°<α<180°),得到图2,请判断:
(1)中的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)在正方形OEFG旋转过程中,请直接写出:
①当α=30°时,∠OAG的度数;
②当△AEG的面积最小时,旋转角α的度数.
-参考答案-
一、单选题
1、D
【解析】
【分析】
正确的命题是真命题,根据定义解答.
【详解】
解:A. 三角形的外心是三角形三条边垂直平分线的交点,故该项不符合题意;
B. 满足的三个正整数,,是勾股数,故该项不符合题意;
C. 对角线相等的四边形各边中点连线所得四边形是菱形,故该项不符合题意;
D. 五边形的内角和为,故该项符合题意;
故选:D.
【点睛】
此题考查了真命题的定义,正确掌握三角形外心的定义,勾股数的定义,中点四边形的判定定理及多边形内角和的计算公式是解题的关键.
2、C
【解析】
【分析】
根据矩形的判定:(1)四个角均为直角;(2)对边互相平行且相等;(3)对角线相等且平分,据此即可判断结果.
【详解】
解:A、根据矩形的对角线相等且平分,故错误;
B、对边分别相等只能判定四边形是平行四边形,故错误;
C、矩形的四个角都是直角,故正确;
D、矩形的对角线互相相等且平分,所以垂直与否与矩形的判定无关,故错误.
故选:C.
【点睛】
本题主要考查的是矩形的判定方法,熟练掌握矩形的判定是解题的关键.
3、A
【解析】
【分析】
利用正方形的性质证明∠DBC=45°和BE=BC,进而证明∠BEC=67.5°.
【详解】
解:∵四边形ABCD是正方形,
∴BC=AD,∠DBC=45°,
∵BE=AD,
∴BE=BC,
∴∠BEC=∠BCE=(180°﹣45°)÷2=67.5°,
∵AC⊥BD,
∴∠COE=90°,
∴∠ACE=90°﹣∠BEC=90°﹣67.5°=22.5°,
故选:A.
【点睛】
本题考查正方形的性质,以及等腰三角形的性质,掌握正方形的性质并加以利用是解决本题的关键.
4、C
【解析】
【分析】
依题意得出AE=AB=AD,∠ADE=50°,又因为∠B=80°故可推出∠ADC=80°,∠CDE=∠ADC-∠ADE,从而求解.
【详解】
∵ADBC,
∴∠AEB=∠DAE=∠B=80°,
∴AE=AB=AD,
在三角形AED中,AE=AD,∠DAE=80°,
∴∠ADE=50°,
又∵∠B=80°,
∴∠ADC=80°,
∴∠CDE=∠ADC-∠ADE=30°.
故选:C.
【点睛】
考查菱形的边的性质,同时综合利用三角形的内角和及等腰三角形的性质,解题关键是利用等腰三角形的性质求得∠ADE的度数.
5、B
【解析】
【分析】
先证明四边形BCED为平行四边形,再根据矩形的判定进行解答.
【详解】
解:∵四边形ABCD为平行四边形,
∴AD∥BC,且AD=BC,
又∵AD=DE,
∴DE∥BC,且DE=BC,
∴四边形BCED为平行四边形,
A、∵AB=BE,DE=AD,
∴BD⊥AE,
∴□DBCE为矩形,故本选项不符合题意;
B、∵DE⊥DC,
∴∠EDB=90°+∠CDB>90°,
∴四边形DBCE不能为矩形,故本选项符合题意;
C、∵∠ADB=90°,
∴∠EDB=90°,
∴□DBCE为矩形,故本选项不符合题意;
D、∵CE⊥DE,
∴∠CED=90°,
∴□DBCE为矩形,故本选项不符合题意.
故选:B.
【点睛】
本题考查了平行四边形的判定和性质、矩形的判定等知识,判定四边形BCED为平行四边形是解题的关键.
6、B
【解析】
【分析】
先根据折叠的性质得到,,设,利用两点间的距离公式得到,,解关于、的方程组得到点的坐标为,,再利用待定系数法求出直线的解析式为,易得直线的解析式为,解方程组得,,然后根据反比例函数图象上点的坐标特征求的值.
【详解】
解:正方形的边长为4,点是边的中点,
,,,,
沿着折叠得到,
,,
设,
,
,
,,
点的坐标为,,
设直线的解析式为,
把,,分别代入得,
解得,
直线的解析式为,
易得直线的解析式为,
解方程组得,
,,
点,在反比例函数的图象上,
.
故选:B.
【点睛】
本题考查了反比例函数图象上点的坐标特征,解题的关键是掌握反比例函数为常数,的图象是双曲线,图象上的点的横纵坐标的积是定值,即.也考查了正方形的性质和折叠的性质.
7、B
【解析】
【分析】
由菱形的性质得AB=BC=2(cm),OA=OC,OB=OD,AC⊥BD,再证△ABC是等边三角形,得AC=AB=2(cm),则OA=1(cm),然后由勾股定理求出OB=(cm),即可求解.
【详解】
解:∵菱形ABCD的周长为8cm,
∴AB=BC=2(cm),OA=OC,OB=OD,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2cm,
∴OA=1(cm),
在Rt△AOB中,由勾股定理得:OB===(cm),
∴BD=2OB=2(cm),
故选:B.
【点睛】
此题考查了菱形的性质,勾股定理,等边三角形的性质和判定,解题的关键是熟练掌握菱形的性质,勾股定理,等边三角形的性质和判定方法.
8、D
【解析】
【分析】
由题意依据全等三角形的判定得出△BOM≌△CON,进而根据正方形的性质即可得出的大小.
【详解】
解:∵正方形ABCD的对角线AC,BD交于点O,
∴OC=OD=BO=AO,∠ABO=∠ACB=45°,AC⊥BD.
∵∠MOB+∠BON=90°,∠BON+∠CON=90°
∴∠BOM=∠CON,且OC=OB,∠ABO=∠ACB=45°,
∴△BOM≌△CON(ASA),=S△BOM,
∴,
∵=S正方形ABCD,正方形的边长,,
∴=S正方形ABCD -=.
故选:D.
【点睛】
本题考查正方形的性质以及全等三角形的判定和性质等知识,灵活运用这些性质进行推理是解答本题的关键.
9、B
【解析】
【分析】
利用多边形的内角和公式、三角形的三边关系、平行线的性质及菱形的判定分别判断后即可确定正确的选项.
【详解】
解:A、五边形的内角和为540°,故原命题错误,是假命题,不符合题意;
B、三角形的任意两边之和大于第三边,正确,是真命题,符合题意;
C、两直线平行,内错角相等,故原命题错误,是假命题,不符合题意;
D、对角线互相垂直的平行四边形是菱形,故原命题错误,是假命题,不符合题意,
故选:B.
【点睛】
本题考查了命题与定理的知识,解题的关键是了解多边形的内角和公式、三角形的三边关系、平行线的性质及菱形的判定等知识,难度不大.
10、A
【解析】
【分析】
利用等式的性质以及矩形、正方形、菱形的判定方法分别判断后即可确定正确的选项.
【详解】
解:A、若,则,故此命题正确;
B、四条边相等的四边形是菱形,故原命题不正确;
C、有一组邻边相等的平行四边形是菱形,故原命题不正确;
D、如果,a≠0时,则,若时,此命题不正确,
故选:A.
【点睛】
本题考查了命题与定理以及等式的性质等知识,解题的关键是了解矩形及菱形的判定方法.
二、填空题
1、
【解析】
【分析】
连接AN交BM于点O,过点N作NH⊥AD于点H,根据正方形的性质可得AM=3,DM=6,从而得到,再由轴对称图形的性质,可得AN⊥BM,AO=NO,MN=AM=3,再由,可得,从而得到,再由勾股定理可得,从而得到,进而得到, ,即可求证.
【详解】
解:如图,连接AN交BM于点O,过点N作NH⊥AD于点H,
∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵, .
∴AM=3,DM=6,
∴ ,
∵将△BMA沿BM对折至△BMN,
∴AN⊥BM,AO=NO,MN=AM=3,
∵ ,
∴ ,
∴,
在 中,由勾股定理得:
,
在 中,由勾股定理得:
,
∴,
即 ,解得: ,
∴ , ,
∴ ,
∴ .
故答案为:
【点睛】
本题主要考查了正方形与折叠问题,勾股定理,轴对称图形的性质,熟练掌握相关知识点是解题的关键.
2、144
【解析】
【分析】
根据将纸片沿折叠,使点B落在边上的点处,得出∠EB′F=∠B=90°,∠BFE=∠B′FE,可得∠AB′E+∠DB′F=90°根据四边形ABCD为矩形,得出AD∥BC,可得∠DBF=∠B′FB=2∠EFB,可求∠AB′E =90°-∠DB′F=90°-2∠EFB,根据GH为对称轴,可得∠CB′F=∠CFB′=180°-∠B′FB=180°-2∠EFB,可得∠C′B′D=∠C′B′F-∠FB′D=180°-2∠EFB-2∠EFB,根据,列方程180°-2∠EFB-2∠EFB-(90°-2∠EFB)=18°,解方程即可.
【详解】
解:∵将纸片沿折叠,使点B落在边上的点处,
∴∠EB′F=∠B=90°,∠BFE=∠B′FE,
∴∠AB′E+∠DB′F=90°
∴∠AB′E =90°-∠DB′F
∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DB′F=∠B′FB=2∠EFB,
∴∠AB′E =90°-∠DBF=90°-2∠EFB,
∵GH为对称轴,
∴∠C′B′F=∠CFB′=180°-∠B′FB=180°-2∠EFB,
∵∠C′B′D=∠C′B′F-∠FB′D=180°-2∠EFB-2∠EFB,
∵,
∴180°-2∠EFB-2∠EFB-(90°-2∠EFB)=18°,
解得∠EFB=36°,
∴∠EFC=180°-∠EFB=180°-36°=144°.
故答案为144.
【点睛】
本题考查折叠性质,矩形性质,平行线性质,补角性质,列一元一次方程,掌握折叠性质,矩形性质,平行线性质,补角性质,列一元一次方程是解题关键.
3、
【解析】
【分析】
连接AC,根据菱形的性质及等边三角形的性质证明△ABE≌△ACF(ASA),得到S△ABE=S△ACF,进而得到四边形AECF的面积=S△ABC,过点A作AH⊥BC于H,由勾股定理求出AH,再利用三角形面积公式计算即可.
【详解】
解:连接AC,
∵四边形ABCD为菱形,∠BAD=120°,
∴∠1+∠EAC=60°,
∵为等边三角形,
∴∠3+∠EAC=60°,
∴∠1=∠3,
∵∠BAD=120°,
∴∠ABC=60°,
∴△ABC和△ACD为等边三角形,
∴∠4=60°,AC=AB,
∴△ABE≌△ACF(ASA),
∴S△ABE=S△ACF,
∴四边形AECF的面积=S△ABC,
过点A作AH⊥BC于H,则∠BAH=30°,
∴,
∴,
∴四边形AECF的面积=S△ABC=,
故答案为:.
【点睛】
此题考查了菱形的性质,等边三角形的性质,勾股定理,全等三角形的判定及性质,熟记菱形的性质及全等三角形的判定是解题的关键.
4、
【解析】
【分析】
由图知,四边形ABCD的面积=4个直角三角形面积的和+正方形EFGH的面积,由题意可求得直角三角形的面积及正方形EFGH的面积,从而可求得结果.
【详解】
∵四边形EFGH是正方形
∴GH=EF=2
∵△ABH≌△BCG
∴BG=AH=6
∴BH=BG+GH=6+2=8
∴
∵ △ABH、△BCG、△CDF和△DAE是四个全等的直角三角形
∴这四个直角三角形的面积均为24
∵四边形EFGH是正方形
∴
∴
故答案为:100
【点睛】
本题考查了正方形的性质、全等三角形的性质及图形的面积,关键是全等三角形的性质求得直角三角形的面积.
5、2
【解析】
【分析】
过点D作DM⊥CB于M,证出∠DAE=∠DBM,判定△ADE≌△BDM,得到DM=DE=3,证明四边形CEDM是矩形,得到CE=DM=3,由AE=1,求出BC=AC=2.
【详解】
解:∵DE⊥AC,
∴∠E=∠C=90°,
∴,
过点D作DM⊥CB于M,则∠M=90°=∠E,
∵AD=BD,
∴∠BAD=∠ABD,
∵AC=BC,
∴∠CAB=∠CBA,
∴∠DAE=∠DBM,
∴△ADE≌△BDM,
∴DM=DE=3,
∵∠E=∠C=∠M =90°,
∴四边形CEDM是矩形,
∴CE=DM=3,
∵AE=1,
∴BC=AC=2,
故答案为:2.
【点睛】
此题考查了全等三角形的判定及性质,矩形的判定及性质,等边对等角证明角度相等,正确引出辅助线证明△ADE≌△BDM是解题的关键.
三、解答题
1、(1)见解析;(2)FC=3.
【解析】
【分析】
(1)由旋转可得DE=DM,∠EDM为直角,可得出∠EDF+∠MDF=90°,由∠EDF=45°,得到∠MDF为45°,可得出∠EDF=∠MDF,再由DF=DF,利用SAS可得出三角形DEF与三角形MDF全等,由全等三角形的对应边相等可得出EF=MF;
(2)由(1)的全等得到AE=CM=2,正方形的边长为6,用AB﹣AE求出EB的长,再由BC+CM求出BM的长,设EF=MF=x,可得出BF=BM﹣FM=BM﹣EF=8﹣x,在直角三角形BEF中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即为EF的长,由此即可求出CF的长.
【详解】
解:(1)∵四边形ABCD是正方形,
∴∠A=∠FCD=∠ADC=90°,
∵△DAE逆时针旋转90°得到△DCM,
∴∠A=∠DCM=90°,AE=CM,∠ADE=∠CDM,DE=DM
∴∠FCD+∠DCM=180°,∠ADE+∠EDC=∠CDM+∠EDC=90°,
∴F、C、M三点共线,∠EDM=90°,
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,
∴∠FDM=∠EDF=45°,
在△DEF和△DMF中,
∵,
∴△DEF≌△DMF(SAS),
∴EF=MF;
(2)设EF=MF=x,
∵AE=CM=2,且BC=6,
∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4,
在Rt△EBF中,由勾股定理得,
即,
解得:x=5,
∴EF=5,
∴CF=FM-CM=EF-CM=3.
【点睛】
本题主要考查正方形的性质、旋转的性质、三角形全等及勾股定理,关键是根据半角旋转得到三角形的全等,然后利用勾股定理求得线段的长.
2、(1)见解析;(2)见解析
【解析】
【分析】
(1)根据平行四边形的性质可得ABCD且AB=CD,进而证明∠BEF=∠FDC,∠FBE=∠FCD, ASA证明△BEF≌△CDF.
(2)根据等边对等角证明FD=FC,进而证明,根据对角线相等的平行四边形是矩形即可证明
【详解】
(1)∵四边形ABCD为平行四边形,
∴ABCD且AB=CD.
∵BE=AB,
∴BECD且BE=CD.
∴∠BEF=∠FDC,∠FBE=∠FCD,
∴△BEF≌△CDF.
(2)∵BECD且BE=CD.
∴四边形BECD为平行四边形,
∴DF=DE,CF=BC,
∵四边形ABCD为平行四边形,
∴∠FCD=∠A,
∵∠BFD=∠FCD+∠FDC,∠BFD=2∠A,
∴∠FDC=∠FCD,
∴FD=FC.
又DF=DE,CF=BC,
∴BC=DE,
∴ BECD是矩形.
【点睛】
本题考查了平行四边形的性质与判定,矩形的判定,三角形全等的性质与判定,掌握平行四边形的性质与判定是解题的关键.
3、 (1)“翻移运动”对应点(指图1中的与,与连线被翻移线平分
(2)3
(3)11或10
【解析】
【分析】
(1)画出图形,即可得出结论;
(2)作直线,即为“翻移线”直线,再由“翻移运动”的性质和三角形面积关系求解即可;
(3)分两种情况:①先按(2)的“翻移线”直线翻折,然后再向上平移2个单位,②先按(2)的“翻移线”直线翻折,然后再向下平移2个单位,由“翻移运动”的性质、梯形面积公式和三角形面积公式分别求解即可.
(1)
解:如图1,连接,,
则“翻移运动”对应点(指图1中的与,与连线被翻移线平分;
(2)
解:作直线,即为“翻移线”直线,如图2所示:
四边形是长方形,
,,
由“翻移运动”的性质得:,,是的中点,
,
,
,
,
,
,
;
(3)
解:分两种情况:
①先按(2)的“翻移线”直线翻折,然后再向上平移2个单位,如图3所示:
设翻折后的三角形为,连接,
则,
同(2)得:,,
,,
,
四边形的面积梯形的面积的面积的面积;
②先按(2)的“翻移线”直线翻折,然后再向下平移2个单位,如图4所示:
设翻折后的三角形为,连接,
则,
同(2)得:,,
,,
,
四边形的面积梯形的面积的面积的面积;
综上所述,四边形的面积为11或10.
【点睛】
本题是四边形综合题目,考查了长方形的性质、“翻移运动”的性质、梯形面积公式、三角形面积公式等知识,本题综合性强,解题的关键是熟练掌握“翻移运动”的性质和长方形的性质.
4、(1)AG=DE;(2)成立,理由见解析;(3)①90°,②135°
【解析】
【分析】
(1)证明△AOG≌△DOE(SAS),得出AG=DE即可;
(2)先证明∠AOG=∠DOE,再证明△AOG≌△DOE(SAS),得出AG=DE即可;
(3)①过点E作EM⊥AC交AC的延长线于点M,证明△AOG≌△DOE,则可得出答案;
②作AH⊥GE于H,连接OH,则当O、A、H在同一直线上时OH最小,然后根据旋转的性质可得出答案.
【详解】
(1)证明:∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∴∠AOG=∠DOE=90°,
∵四边形OEFG是正方形,
∴OG=OE,
在△AOG和△DOE中
,
∴△AOG≌△DOE(SAS),
∴AG=DE;
(2)成立,理由:
∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∴∠AOD=∠DOC=90°,
∵∠DOG=∠COE=α,
∴∠AOG=∠DOE,
∵四边形OEFG是正方形,
∴OG=OE,
在△AOG和△DOE中
,
∴△AOG≌△DOE(SAS),
∴AG=DE;
(3)①过点E作EM⊥AC交AC的延长线于点M,则∠EMO=90°,
由旋转的性质可知∠MOE=∠DOG=α=30°,
∴∠MOE=90°-30°=60°,
∵点O是正方形ABCD两对角线的交点,
∴OA⊥OD,
∴∠AOG=90°-30°=60°,
∴∠AOG =∠MOE,
在△AOG和△DOE中
,
∴△AOG≌△DOE(SAS),
∴∠OAG=∠EMO=90°;
②作AH⊥GE于H,连接OH,
∵OG=2OD,OE=2OC,
∴OG、OE为定值,
∴GE=是定值,
∴当AH最小时,△AEG的面积最小,
∵当O、A、H在同一直线上时OH最小,OA为定值,
∴此时AH最小,即△AEG的面积最小,
此时的旋转角α=∠HOG+∠AOD=45°+90°=135°.
【点睛】
本题考查了正方形的性质,全等三角形的判定与性质,勾股定理,旋转的性质等知识,熟练掌握旋转的性质及证明三角形全等是解决问题的关键.
