人教版数学九年级下册第二十七章相似必考点解析试卷(含解析)
文档属性
| 名称 | 人教版数学九年级下册第二十七章相似必考点解析试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 645.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 15:52:49 | ||
图片预览


文档简介
人教版数学九年级下册第二十七章相似必考点解析
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,在Rt中,,,,在Rt中,,点在上,交于点,交于点,当时,的长为( )
A.4 B.6 C. D.
2、如图,点E,D,F在△ABC的三边上,四边形AEDF是菱形,若,则的值为( )
A. B. C. D.
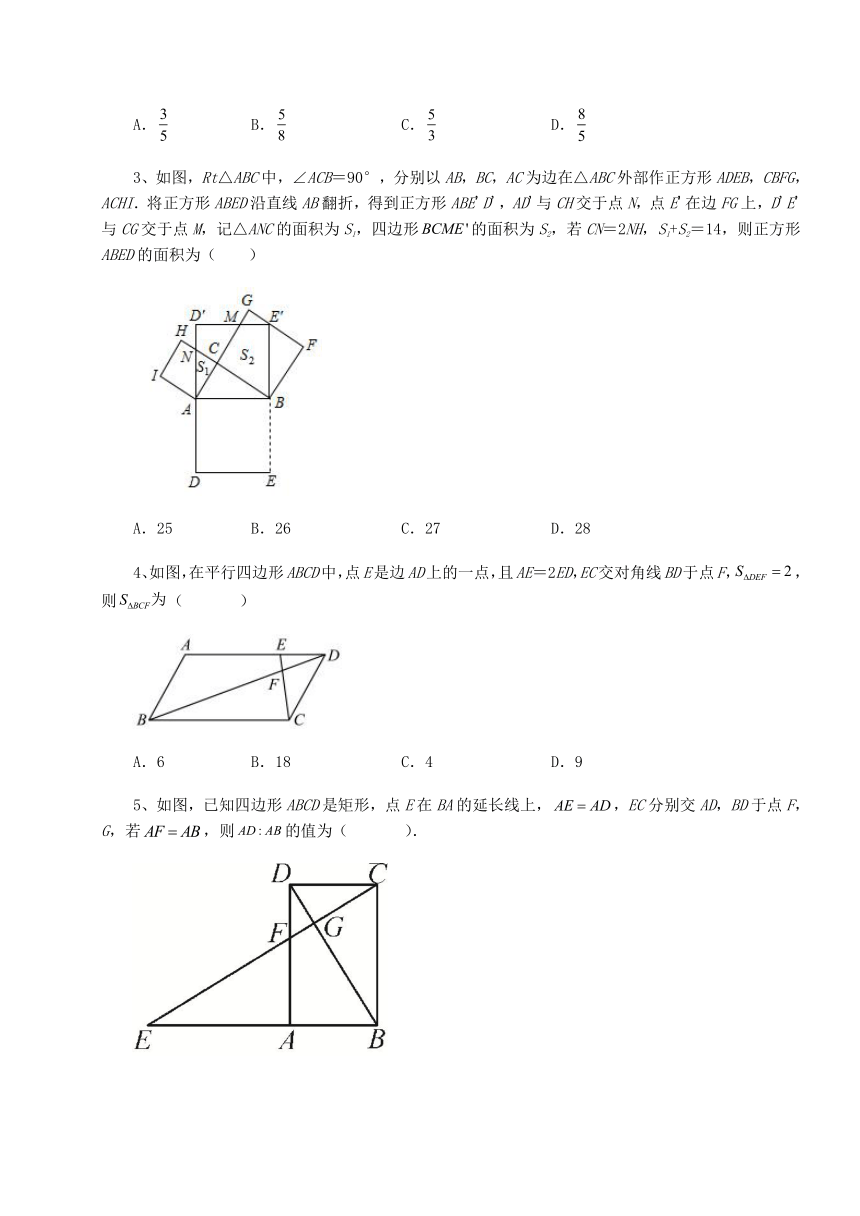
3、如图,Rt△ABC中,∠ACB=90°,分别以AB,BC,AC为边在△ABC外部作正方形ADEB,CBFG,ACHI.将正方形ABED沿直线AB翻折,得到正方形ABE'D',AD'与CH交于点N,点E'在边FG上,D'E'与CG交于点M,记△ANC的面积为S1,四边形的面积为S2,若CN=2NH,S1+S2=14,则正方形ABED的面积为( )
A.25 B.26 C.27 D.28
4、如图,在平行四边形ABCD中,点E是边AD上的一点,且AE=2ED,EC交对角线BD于点F,,则( )
A.6 B.18 C.4 D.9
5、如图,已知四边形ABCD是矩形,点E在BA的延长线上,,EC分别交AD,BD于点F,G,若,则的值为( ).
A. B. C.2 D.
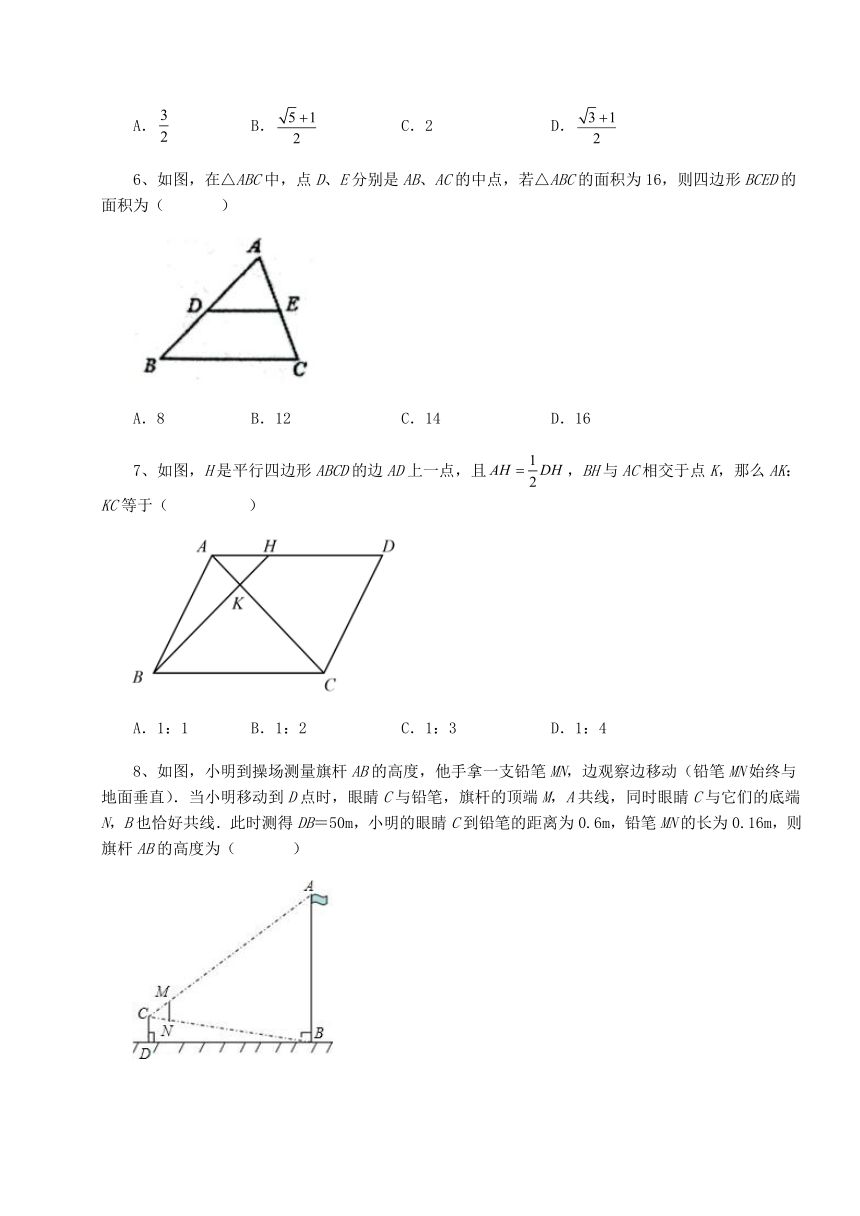
6、如图,在△ABC中,点D、E分别是AB、AC的中点,若△ABC的面积为16,则四边形BCED的面积为( )
A.8 B.12 C.14 D.16
7、如图,H是平行四边形ABCD的边AD上一点,且,BH与AC相交于点K,那么AK:KC等于( )
A.1:1 B.1:2 C.1:3 D.1:4
8、如图,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直).当小明移动到D点时,眼睛C与铅笔,旗杆的顶端M,A共线,同时眼睛C与它们的底端N,B也恰好共线.此时测得DB=50m,小明的眼睛C到铅笔的距离为0.6m,铅笔MN的长为0.16m,则旗杆AB的高度为( )
A.15m B.m C.m D.14m
9、如图,点P是 ABCD边AD上的一点,E,F分别是BP,CP的中点,已知 ABCD面积为16,那么△PEF的面积为( )
A.8 B.6 C.4 D.2
10、如图,是的重心,过的一条直线分别与AB、AC相交于G、H(均不与的顶点重合),,分别表示四边形和的面积,则的最大值是( )
A. B.1 C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题6分,共计30分)
1、已知B是线段AC的黄金分割点,AB>BC,若AC=6,则AB的长为______.(结果保留根号)
2、如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,F为AB上的点,联结CF.将△ACF沿直线CF翻折,点A的对称点为E,若EF∥CB,则FE=_______________
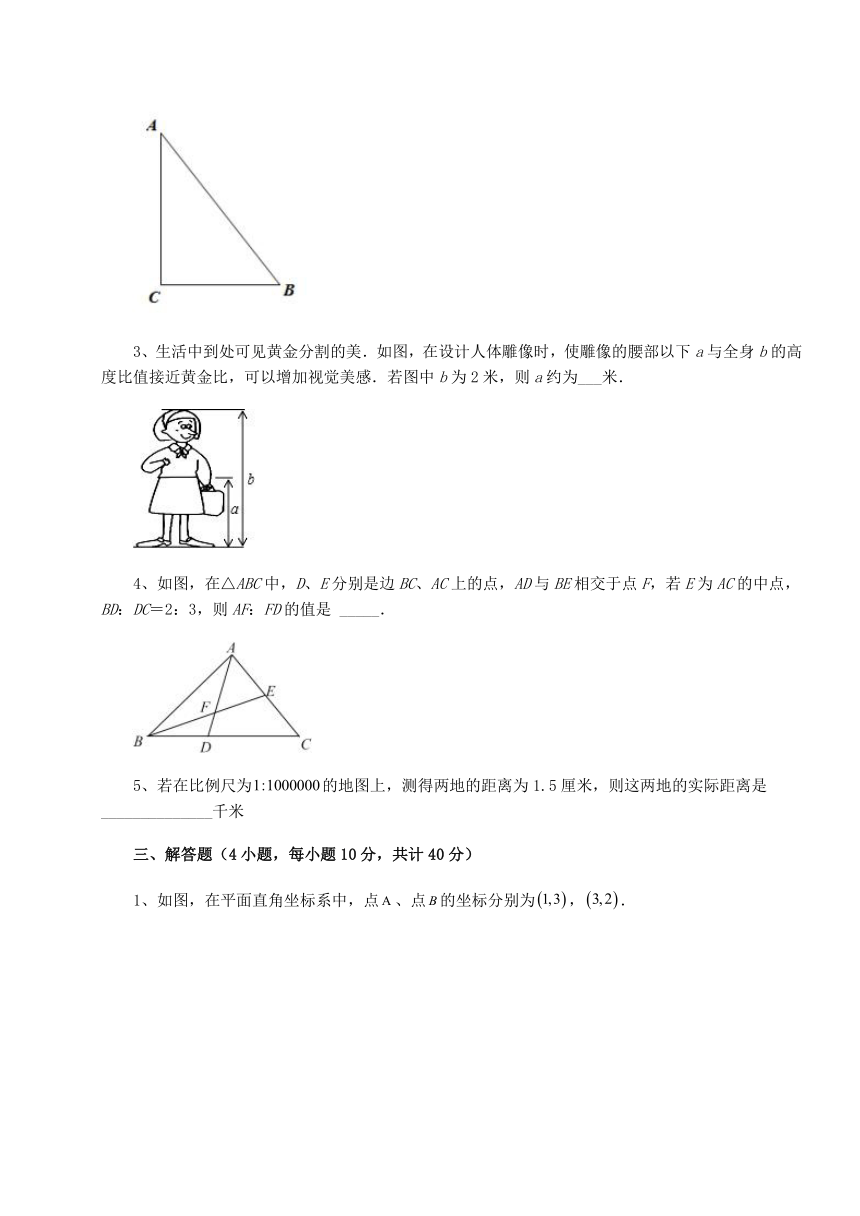
3、生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近黄金比,可以增加视觉美感.若图中b为2米,则a约为___米.
4、如图,在△ABC中,D、E分别是边BC、AC上的点,AD与BE相交于点F,若E为AC的中点,BD:DC=2:3,则AF:FD的值是 _____.
5、若在比例尺为的地图上,测得两地的距离为1.5厘米,则这两地的实际距离是______________千米
三、解答题(4小题,每小题10分,共计40分)
1、如图,在平面直角坐标系中,点、点的坐标分别为,.
(1)画出绕点顺时针旋转后的;
(2)以点为位似中心,相似比为,在轴的上方画出放大后的;
2、图①、图②均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.的顶点均在格点上,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹,不要求写出画法.
(1)在图①中的线段上找一点,连结,使.
(2)在图②中的线段上找一点,连结,使.
3、如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.
(1)作出关于x轴对称的;
(2)以坐标原点为位似中心在图中的网格中作出的位似图形,使与的位似比为1:2;
(3)若的面积为3.5平方单位,求出的面积.
4、如图,过矩形ABCD(AD>AB)的对角线AC的中点O作AC的垂直平分线EF,分别交AD、BC于点E、F,分别连接AF和CE.
(1)判断四边形AFCE是什么特殊四边形,并证明;
(2)过点E作AD的垂线交AC于点P,求证:2AE2=AC AP.
-参考答案-
一、单选题
1、B
【解析】
【分析】
如图作PQ⊥AB于Q,PR⊥BC于R.由△QPE∽△RPF,推出,可得PQ=2PR=2BQ,由PQ//BC,可得AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,可得2x+3x=6,求出x即可解决问题.
【详解】
解:如图作PQ⊥AB于Q,PR⊥BC于R.
∵∠PQB=∠QBR=∠BRP=90°,
∴四边形PQBR是矩形,
∴∠QPR=90°=∠MPN,
∴∠QPE=∠RPF,
∴△QPE∽△RPF,
∴,
∴PQ=2PR=2BQ,
∵PQ//BC,
∴△AQP∽△ABC,
∴AQ:QP:AP=AB:BC:AC=3:4:5,
设PQ=4x,则AQ=3x,AP=5x,BQ=2x,
∴2x+3x=6,
∴x=,
∴AP=5x=6.
故选:B.
【点睛】
本题考查相似三角形的判定和性质、勾股定理、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题.
2、C
【解析】
【分析】
根据菱形的性质可得,进而可得,进而可得
【详解】
解:点E,D,F在△ABC的三边上,四边形AEDF是菱形,
,
,
故选C
【点睛】
本题考查了菱形的性质,平行线分线段成比例,掌握平行线分线段成比例是解题的关键.
3、B
【解析】
【分析】
设,则,证明,得出,根据,再证明,得出,可以得出,得出等式,求解即可得到.
【详解】
解:设,则,
由题意知:,
在和中,
,
,
,
,
,
,
在中由勾股定理得:
,
,
,
在和中,
,
,
,
,
,
,
解得:,
,
故选:B.
【点睛】
本题考查正方形的性质、三角形相似、三角形全等、勾股定理,解题的关键是掌握相应的判定定理,通过转化的思想及等量代换的思想进行求解.
4、B
【解析】
【分析】
先求解,再利用平行四边形的性质证明,得到,再利用相似三角形面积比等于相似比的平方得出两个三角形的面积关系可得答案.
【详解】
解:∵AE=2ED,AD=AE+DE=3DE,
∴ ,
∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD,
∴∠DEF=∠BCF,∠EDF=∠CBF,
,
,
∴,
,
.
故选:B.
【点睛】
本题主要考查了相似三角形的判定与性质,平行四边形的性质,相似两个三角形的面积之间的关系,掌握以上知识是解题的关键.
5、B
【解析】
【分析】
由矩形可证得,则,设AB=AF=CD=x ,AE=AD=y,即可求得的值.
【详解】
∵四边形ABCD是矩形
∴∠DCE=∠AEC,∠CDA=∠EAD
∴
∴
设AB=AF=CD=x ,AE=AD=y,
则有
给方程两边同时除以,
令为t则有
解得,(舍去)
则t==
则=.
故答案选:B.
【点睛】
本题考查了相似三角形性质及判定,将表示为是解题的关键.
6、B
【解析】
【分析】
直接利用三角形中位线定理得出DE∥BC,DE=BC,再利用相似三角形的判定与性质得出即可.
【详解】
解:∵在△ABC中,点D、E分别是AB、AC的中点,
∴DE∥BC,DE=BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∵=,
∴,
∵S△ABC=16,
∴,
∴S四边形BCED= S△ABC-S△ADE=16-4=12.
故选B.
【点睛】
考查了三角形的中位线以及相似三角形的判定与性质,正确得出△ADE∽△ABC是解题关键.
7、C
【解析】
【分析】
根据AH=DH求出AH:AD即AH:BC的值是1:3,再根据相似三角形对应边成比例求出AK:KC的值.
【详解】
解:∵AH=DH,
∴AH:AD=,
∵四边形ABCD是平行四边形,
∴AD=BC,ADBC,
∴AH:BC=
∴△AHK∽△CBK,
∴
故选:C.
【点睛】
本题考查了相似三角形的判定和性质,平行四边形的性质,比例式的变形是解题的关键.
8、C
【解析】
【分析】
利用相似三角形对应边的比等于对应高的比,过作于,交于,先证四边形是矩形,再明,得出,从而求出.
【详解】
解:过作于,交于,
根据题意 ,
∵,
∴,
∴四边形是矩形,
,
又,
∴∠CMN=∠A,∠CNM=∠CBA,
,
,
,
.
故选择C.
【点睛】
本题考查相似三角形的应用,矩形的判定与性质,三角形相似判定与性质,掌握相似三角形的应用于测量的方法,矩形的判定与性质,三角形相似判定与性质是解题关键.
9、D
【解析】
【分析】
根据平行线间的距离处处相等,得到,根据EF是△PBC的中位线,得到△PEF∽△PBC,EF=,得到计算即可.
【详解】
∵点P是 ABCD边AD上的一点,且 ABCD面积为16,
∴;
∵E,F分别是BP,CP的中点,
∴EF∥BC,EF=,
∴△PEF∽△PBC,
∴,
∴,
故选D.
【点睛】
本题考查了平行四边形的性质,三角形中位线定理,三角形相似的判定和性质,熟练掌握中位线定理,灵活运用三角形相似的性质是解题的关键.
10、A
【解析】
【分析】
根据是的重心可得,过O作MN∥BC交AN于N,交AC于M,过M作ME∥AB交GH于E,易证OM=ON,设,分别表示出四边形和的面积即可
【详解】
过O作MN∥BC交AN于N,交AC于M,过M作ME∥AB交GH于E
∵是的重心,
∴,D是BC中点
∴BD=CD,
∵MN∥BC
∴
∴,
∴
∵ME∥AB
∴
∴
∴
设
∴
∴
∴
∵x为定值
∴当y越小时值越大
∴当时最大,此时GH∥BC
故选:A
【点睛】
题是几何综合题,以三角形的重心为背景,考查了重心的概念、性质以及应用,考查了相似三角形的性质知识点.解题的关键是表示出
.
二、填空题
1、##
【解析】
【分析】
根据黄金分割的定义得到,把AC=6代入计算即可解题.
【详解】
解:B是线段AC的黄金分割点,
AC=6
2、2
【解析】
【分析】
根据勾股定理求出,由等面积法求出,根据相似三角形判定证明,由性质建立等式求出即可.
【详解】
解:根据题意作图如下:
由勾股定理得:,
根据折叠的性质得:,
,
,
,
,
,
,
,
解得:,
,
,
,
,
即,
解得:,
故答案是:2.
【点睛】
本题考查了折叠问题,三角形相似、勾股定理,解题的关键是添加辅助线,构造相似三角形.
3、﹣1
【解析】
【分析】
由题意得=,以此进行分析计算即可得出答案.
【详解】
解:∵雕像的腰部以下a与全身b的高度比值接近黄金比,
∴=,
∴a=b=×2=(﹣1)米.
故答案为:(﹣1).
【点睛】
本题考查的是黄金分割的概念,注意掌握把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,其中AC=AB.
4、##2.5
【解析】
【分析】
过D作DH∥AC交BE于H,根据相似三角形的性质即可得到结论.
【详解】
解:过D作DH∥AC交BE于H,
∴△DHF∽△AEF,△BDH∽△BCE,
∴,,
∵若E为AC的中点,
∴CE=AE,
∴,
∵BD:DC=2:3,
∴BD:BC=2:5,
∴DF:AF=2:5,
∴AF:FD=.
故答案为:.
【点睛】
本题考查了三角形相似的判定和性质,合理添加辅助线,正确选择比例式是解题的关键.
5、15
【解析】
【分析】
设两地间的实际距离是xcm,由在比例尺为1:1000 000的地图上,量得两地间的距离为1.5厘米,即可得方程 ,解方程即可求得x的值,然后换算单位即可求得答案.
【详解】
解:设两地间的实际距离是xcm,
∵比例尺为1:1000 000,量得两地间的距离为1.5cm,
∴,
解得:x=1500000,
∵1500000cm=15km,
∴两地间的实际距离是15千米,
故答案为:15.
【点睛】
本题考查了比例的性质——比例尺的性质,解题的关键是根据题意列方程,要注意统一单位.
三、解答题
1、(1)见解析;(2)见解析
【解析】
【分析】
(1)找到绕点顺时针旋转后的对应点,顺次连接,则即为所求;
(2)延长至,至,使得,连接,则即为所求
【详解】
(1)如图,找到绕点顺时针旋转后的对应点,顺次连接,则即为所求;
(2)如图,延长至,至,使得,连接,则
【点睛】
本题考查了画旋转图形,在平面直角坐标系中画位似图形,掌握旋转的性质和位似图形的性质是解题的关键.
2、(1)见解析;(2)见解析
【解析】
【分析】
(1)找出所在的矩形ACBE,然后连接CE,交AB于点D,根据矩形的对角线相等且互相平分即可证明,即点D即为所求;
(2)取格点D、F,连接DF,交AB于点E,连接CE,根据相似三角形的判定及性质可得:,根据勾股定理求出,由线段比例可得:,得出,由等边对等角即可得出两个角相等,即点即为所求.
【详解】
解:(1)如图1,找出所在的矩形ACBE,然后连接CE,交AB于点D,即为所求;
∵四边形ACBE为矩形,
∴,
∴,
∴点D符合题意;
(2)如图2,取格点D、F,连接DF,交AB于点E,连接CE,点即为所求,
∵,
∴,
∴,
在中,,,
∴,
∴,
∴,
∴,
∴点E符合题意.
【点睛】
本题考查作图-应用与设计作图,包括矩形的性质,相似三角形的判定和性质,等腰三角形的性质等,理解题意,熟练掌握运用这些知识点作出相应图形是解题关键.
3、(1)见解析;(2)见解析;(3)14平方单位.
【解析】
【分析】
(1)根据轴对称性质即可画出△ABC关于x轴对称的;
(2)根据位似图形的性质即可画出以点O为位似中心的位似图形,与的位似比为1:2;
(3)利用相似三角形的性质计算即可.
【详解】
解:(1)如图,,即为所求作;
(2)如图,,即为所求作;
(3)∵与的位似比为1:2,
∴∽,,
∴,
∵的面积为3.5平方单位,即的面积为3.5平方单位,
∴的面积为:2=4×3.5=14平方单位.
【点睛】
本题考查了作图-轴对称变换,位似变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4、(1)四边形AFCE是菱形,见解析;(2)见解析
【解析】
【分析】
(1)由过矩形ABCD(AD>AB)的对角线AC的中点O作AC的垂直平分线EF,易证得△AOE≌△COF,即可得EO=FO,则可证得四边形AFCE是平行四边形,又由EF⊥AC,可得四边形AFCE是菱形;
(2)由∠AEP=∠AOE=90°,∠EAP=∠OAE,可证得△AOE∽△AEP,又由相似三角形的对应边成比例,即可证得2AE2=AC AP.
【详解】
证明:(1)四边形AFCE是菱形.
理由:由已知可知:AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴EO=FO,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵∠AEP=∠AOE=90°,∠EAP=∠OAE,
∴△AOE∽△AEP,
∴=,
∴AE2=AO AP,
又AC=2AO,
∴2AE2=AC AP.
【点睛】
本题考查了相似三角形的判定与性质、平行四边形的判定与性质、矩形的性质、菱形的判定与性质以及全等三角形的判定与性质.注意掌握数形结合思想的应用.
考试时间:90分钟;命题人:数学教研组
考生注意:
1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟
2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)
一、单选题(10小题,每小题3分,共计30分)
1、如图,在Rt中,,,,在Rt中,,点在上,交于点,交于点,当时,的长为( )
A.4 B.6 C. D.
2、如图,点E,D,F在△ABC的三边上,四边形AEDF是菱形,若,则的值为( )
A. B. C. D.
3、如图,Rt△ABC中,∠ACB=90°,分别以AB,BC,AC为边在△ABC外部作正方形ADEB,CBFG,ACHI.将正方形ABED沿直线AB翻折,得到正方形ABE'D',AD'与CH交于点N,点E'在边FG上,D'E'与CG交于点M,记△ANC的面积为S1,四边形的面积为S2,若CN=2NH,S1+S2=14,则正方形ABED的面积为( )
A.25 B.26 C.27 D.28
4、如图,在平行四边形ABCD中,点E是边AD上的一点,且AE=2ED,EC交对角线BD于点F,,则( )
A.6 B.18 C.4 D.9
5、如图,已知四边形ABCD是矩形,点E在BA的延长线上,,EC分别交AD,BD于点F,G,若,则的值为( ).
A. B. C.2 D.
6、如图,在△ABC中,点D、E分别是AB、AC的中点,若△ABC的面积为16,则四边形BCED的面积为( )
A.8 B.12 C.14 D.16
7、如图,H是平行四边形ABCD的边AD上一点,且,BH与AC相交于点K,那么AK:KC等于( )
A.1:1 B.1:2 C.1:3 D.1:4
8、如图,小明到操场测量旗杆AB的高度,他手拿一支铅笔MN,边观察边移动(铅笔MN始终与地面垂直).当小明移动到D点时,眼睛C与铅笔,旗杆的顶端M,A共线,同时眼睛C与它们的底端N,B也恰好共线.此时测得DB=50m,小明的眼睛C到铅笔的距离为0.6m,铅笔MN的长为0.16m,则旗杆AB的高度为( )
A.15m B.m C.m D.14m
9、如图,点P是 ABCD边AD上的一点,E,F分别是BP,CP的中点,已知 ABCD面积为16,那么△PEF的面积为( )
A.8 B.6 C.4 D.2
10、如图,是的重心,过的一条直线分别与AB、AC相交于G、H(均不与的顶点重合),,分别表示四边形和的面积,则的最大值是( )
A. B.1 C. D.
第Ⅱ卷(非选择题 70分)
二、填空题(5小题,每小题6分,共计30分)
1、已知B是线段AC的黄金分割点,AB>BC,若AC=6,则AB的长为______.(结果保留根号)
2、如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,F为AB上的点,联结CF.将△ACF沿直线CF翻折,点A的对称点为E,若EF∥CB,则FE=_______________
3、生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近黄金比,可以增加视觉美感.若图中b为2米,则a约为___米.
4、如图,在△ABC中,D、E分别是边BC、AC上的点,AD与BE相交于点F,若E为AC的中点,BD:DC=2:3,则AF:FD的值是 _____.
5、若在比例尺为的地图上,测得两地的距离为1.5厘米,则这两地的实际距离是______________千米
三、解答题(4小题,每小题10分,共计40分)
1、如图,在平面直角坐标系中,点、点的坐标分别为,.
(1)画出绕点顺时针旋转后的;
(2)以点为位似中心,相似比为,在轴的上方画出放大后的;
2、图①、图②均是的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.的顶点均在格点上,只用无刻度的直尺,在给定的网格中,分别按下列要求画图,保留适当的作图痕迹,不要求写出画法.
(1)在图①中的线段上找一点,连结,使.
(2)在图②中的线段上找一点,连结,使.
3、如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.
(1)作出关于x轴对称的;
(2)以坐标原点为位似中心在图中的网格中作出的位似图形,使与的位似比为1:2;
(3)若的面积为3.5平方单位,求出的面积.
4、如图,过矩形ABCD(AD>AB)的对角线AC的中点O作AC的垂直平分线EF,分别交AD、BC于点E、F,分别连接AF和CE.
(1)判断四边形AFCE是什么特殊四边形,并证明;
(2)过点E作AD的垂线交AC于点P,求证:2AE2=AC AP.
-参考答案-
一、单选题
1、B
【解析】
【分析】
如图作PQ⊥AB于Q,PR⊥BC于R.由△QPE∽△RPF,推出,可得PQ=2PR=2BQ,由PQ//BC,可得AQ:QP:AP=AB:BC:AC=3:4:5,设PQ=4x,则AQ=3x,AP=5x,BQ=2x,可得2x+3x=6,求出x即可解决问题.
【详解】
解:如图作PQ⊥AB于Q,PR⊥BC于R.
∵∠PQB=∠QBR=∠BRP=90°,
∴四边形PQBR是矩形,
∴∠QPR=90°=∠MPN,
∴∠QPE=∠RPF,
∴△QPE∽△RPF,
∴,
∴PQ=2PR=2BQ,
∵PQ//BC,
∴△AQP∽△ABC,
∴AQ:QP:AP=AB:BC:AC=3:4:5,
设PQ=4x,则AQ=3x,AP=5x,BQ=2x,
∴2x+3x=6,
∴x=,
∴AP=5x=6.
故选:B.
【点睛】
本题考查相似三角形的判定和性质、勾股定理、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题.
2、C
【解析】
【分析】
根据菱形的性质可得,进而可得,进而可得
【详解】
解:点E,D,F在△ABC的三边上,四边形AEDF是菱形,
,
,
故选C
【点睛】
本题考查了菱形的性质,平行线分线段成比例,掌握平行线分线段成比例是解题的关键.
3、B
【解析】
【分析】
设,则,证明,得出,根据,再证明,得出,可以得出,得出等式,求解即可得到.
【详解】
解:设,则,
由题意知:,
在和中,
,
,
,
,
,
,
在中由勾股定理得:
,
,
,
在和中,
,
,
,
,
,
,
解得:,
,
故选:B.
【点睛】
本题考查正方形的性质、三角形相似、三角形全等、勾股定理,解题的关键是掌握相应的判定定理,通过转化的思想及等量代换的思想进行求解.
4、B
【解析】
【分析】
先求解,再利用平行四边形的性质证明,得到,再利用相似三角形面积比等于相似比的平方得出两个三角形的面积关系可得答案.
【详解】
解:∵AE=2ED,AD=AE+DE=3DE,
∴ ,
∵四边形ABCD为平行四边形,
∴AD∥BC,BC=AD,
∴∠DEF=∠BCF,∠EDF=∠CBF,
,
,
∴,
,
.
故选:B.
【点睛】
本题主要考查了相似三角形的判定与性质,平行四边形的性质,相似两个三角形的面积之间的关系,掌握以上知识是解题的关键.
5、B
【解析】
【分析】
由矩形可证得,则,设AB=AF=CD=x ,AE=AD=y,即可求得的值.
【详解】
∵四边形ABCD是矩形
∴∠DCE=∠AEC,∠CDA=∠EAD
∴
∴
设AB=AF=CD=x ,AE=AD=y,
则有
给方程两边同时除以,
令为t则有
解得,(舍去)
则t==
则=.
故答案选:B.
【点睛】
本题考查了相似三角形性质及判定,将表示为是解题的关键.
6、B
【解析】
【分析】
直接利用三角形中位线定理得出DE∥BC,DE=BC,再利用相似三角形的判定与性质得出即可.
【详解】
解:∵在△ABC中,点D、E分别是AB、AC的中点,
∴DE∥BC,DE=BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∵=,
∴,
∵S△ABC=16,
∴,
∴S四边形BCED= S△ABC-S△ADE=16-4=12.
故选B.
【点睛】
考查了三角形的中位线以及相似三角形的判定与性质,正确得出△ADE∽△ABC是解题关键.
7、C
【解析】
【分析】
根据AH=DH求出AH:AD即AH:BC的值是1:3,再根据相似三角形对应边成比例求出AK:KC的值.
【详解】
解:∵AH=DH,
∴AH:AD=,
∵四边形ABCD是平行四边形,
∴AD=BC,ADBC,
∴AH:BC=
∴△AHK∽△CBK,
∴
故选:C.
【点睛】
本题考查了相似三角形的判定和性质,平行四边形的性质,比例式的变形是解题的关键.
8、C
【解析】
【分析】
利用相似三角形对应边的比等于对应高的比,过作于,交于,先证四边形是矩形,再明,得出,从而求出.
【详解】
解:过作于,交于,
根据题意 ,
∵,
∴,
∴四边形是矩形,
,
又,
∴∠CMN=∠A,∠CNM=∠CBA,
,
,
,
.
故选择C.
【点睛】
本题考查相似三角形的应用,矩形的判定与性质,三角形相似判定与性质,掌握相似三角形的应用于测量的方法,矩形的判定与性质,三角形相似判定与性质是解题关键.
9、D
【解析】
【分析】
根据平行线间的距离处处相等,得到,根据EF是△PBC的中位线,得到△PEF∽△PBC,EF=,得到计算即可.
【详解】
∵点P是 ABCD边AD上的一点,且 ABCD面积为16,
∴;
∵E,F分别是BP,CP的中点,
∴EF∥BC,EF=,
∴△PEF∽△PBC,
∴,
∴,
故选D.
【点睛】
本题考查了平行四边形的性质,三角形中位线定理,三角形相似的判定和性质,熟练掌握中位线定理,灵活运用三角形相似的性质是解题的关键.
10、A
【解析】
【分析】
根据是的重心可得,过O作MN∥BC交AN于N,交AC于M,过M作ME∥AB交GH于E,易证OM=ON,设,分别表示出四边形和的面积即可
【详解】
过O作MN∥BC交AN于N,交AC于M,过M作ME∥AB交GH于E
∵是的重心,
∴,D是BC中点
∴BD=CD,
∵MN∥BC
∴
∴,
∴
∵ME∥AB
∴
∴
∴
设
∴
∴
∴
∵x为定值
∴当y越小时值越大
∴当时最大,此时GH∥BC
故选:A
【点睛】
题是几何综合题,以三角形的重心为背景,考查了重心的概念、性质以及应用,考查了相似三角形的性质知识点.解题的关键是表示出
.
二、填空题
1、##
【解析】
【分析】
根据黄金分割的定义得到,把AC=6代入计算即可解题.
【详解】
解:B是线段AC的黄金分割点,
AC=6
2、2
【解析】
【分析】
根据勾股定理求出,由等面积法求出,根据相似三角形判定证明,由性质建立等式求出即可.
【详解】
解:根据题意作图如下:
由勾股定理得:,
根据折叠的性质得:,
,
,
,
,
,
,
,
解得:,
,
,
,
,
即,
解得:,
故答案是:2.
【点睛】
本题考查了折叠问题,三角形相似、勾股定理,解题的关键是添加辅助线,构造相似三角形.
3、﹣1
【解析】
【分析】
由题意得=,以此进行分析计算即可得出答案.
【详解】
解:∵雕像的腰部以下a与全身b的高度比值接近黄金比,
∴=,
∴a=b=×2=(﹣1)米.
故答案为:(﹣1).
【点睛】
本题考查的是黄金分割的概念,注意掌握把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,其中AC=AB.
4、##2.5
【解析】
【分析】
过D作DH∥AC交BE于H,根据相似三角形的性质即可得到结论.
【详解】
解:过D作DH∥AC交BE于H,
∴△DHF∽△AEF,△BDH∽△BCE,
∴,,
∵若E为AC的中点,
∴CE=AE,
∴,
∵BD:DC=2:3,
∴BD:BC=2:5,
∴DF:AF=2:5,
∴AF:FD=.
故答案为:.
【点睛】
本题考查了三角形相似的判定和性质,合理添加辅助线,正确选择比例式是解题的关键.
5、15
【解析】
【分析】
设两地间的实际距离是xcm,由在比例尺为1:1000 000的地图上,量得两地间的距离为1.5厘米,即可得方程 ,解方程即可求得x的值,然后换算单位即可求得答案.
【详解】
解:设两地间的实际距离是xcm,
∵比例尺为1:1000 000,量得两地间的距离为1.5cm,
∴,
解得:x=1500000,
∵1500000cm=15km,
∴两地间的实际距离是15千米,
故答案为:15.
【点睛】
本题考查了比例的性质——比例尺的性质,解题的关键是根据题意列方程,要注意统一单位.
三、解答题
1、(1)见解析;(2)见解析
【解析】
【分析】
(1)找到绕点顺时针旋转后的对应点,顺次连接,则即为所求;
(2)延长至,至,使得,连接,则即为所求
【详解】
(1)如图,找到绕点顺时针旋转后的对应点,顺次连接,则即为所求;
(2)如图,延长至,至,使得,连接,则
【点睛】
本题考查了画旋转图形,在平面直角坐标系中画位似图形,掌握旋转的性质和位似图形的性质是解题的关键.
2、(1)见解析;(2)见解析
【解析】
【分析】
(1)找出所在的矩形ACBE,然后连接CE,交AB于点D,根据矩形的对角线相等且互相平分即可证明,即点D即为所求;
(2)取格点D、F,连接DF,交AB于点E,连接CE,根据相似三角形的判定及性质可得:,根据勾股定理求出,由线段比例可得:,得出,由等边对等角即可得出两个角相等,即点即为所求.
【详解】
解:(1)如图1,找出所在的矩形ACBE,然后连接CE,交AB于点D,即为所求;
∵四边形ACBE为矩形,
∴,
∴,
∴点D符合题意;
(2)如图2,取格点D、F,连接DF,交AB于点E,连接CE,点即为所求,
∵,
∴,
∴,
在中,,,
∴,
∴,
∴,
∴,
∴点E符合题意.
【点睛】
本题考查作图-应用与设计作图,包括矩形的性质,相似三角形的判定和性质,等腰三角形的性质等,理解题意,熟练掌握运用这些知识点作出相应图形是解题关键.
3、(1)见解析;(2)见解析;(3)14平方单位.
【解析】
【分析】
(1)根据轴对称性质即可画出△ABC关于x轴对称的;
(2)根据位似图形的性质即可画出以点O为位似中心的位似图形,与的位似比为1:2;
(3)利用相似三角形的性质计算即可.
【详解】
解:(1)如图,,即为所求作;
(2)如图,,即为所求作;
(3)∵与的位似比为1:2,
∴∽,,
∴,
∵的面积为3.5平方单位,即的面积为3.5平方单位,
∴的面积为:2=4×3.5=14平方单位.
【点睛】
本题考查了作图-轴对称变换,位似变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4、(1)四边形AFCE是菱形,见解析;(2)见解析
【解析】
【分析】
(1)由过矩形ABCD(AD>AB)的对角线AC的中点O作AC的垂直平分线EF,易证得△AOE≌△COF,即可得EO=FO,则可证得四边形AFCE是平行四边形,又由EF⊥AC,可得四边形AFCE是菱形;
(2)由∠AEP=∠AOE=90°,∠EAP=∠OAE,可证得△AOE∽△AEP,又由相似三角形的对应边成比例,即可证得2AE2=AC AP.
【详解】
证明:(1)四边形AFCE是菱形.
理由:由已知可知:AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE和△COF中,
,
∴△AOE≌△COF(AAS),
∴EO=FO,
∴四边形AFCE是平行四边形,
∵AC⊥EF,
∴四边形AFCE是菱形;
(2)∵∠AEP=∠AOE=90°,∠EAP=∠OAE,
∴△AOE∽△AEP,
∴=,
∴AE2=AO AP,
又AC=2AO,
∴2AE2=AC AP.
【点睛】
本题考查了相似三角形的判定与性质、平行四边形的判定与性质、矩形的性质、菱形的判定与性质以及全等三角形的判定与性质.注意掌握数形结合思想的应用.
