数学高中北师大版必修四第二章《平面向量》课件
文档属性
| 名称 | 数学高中北师大版必修四第二章《平面向量》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 306.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-10 00:00:00 | ||
图片预览







文档简介
课件70张PPT。平面向量的实际背景及基本概念思考:下列哪些是向量?哪些不是向量?(1)时间;(2)路程;(3)速度;(4)功;(5)加速度;(6)速率;(7)重力;(8)浮力。知识点一 向量的有关概念1.向量:既有大小又有方向的量,向量包括两个要素:
大小、方向。
2.数量:只有大小、没有方向的量
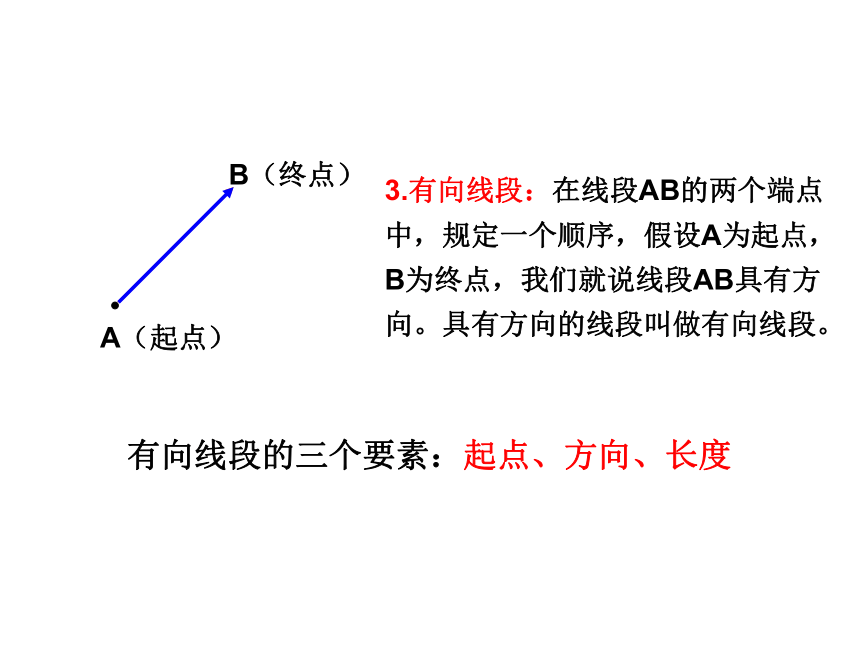
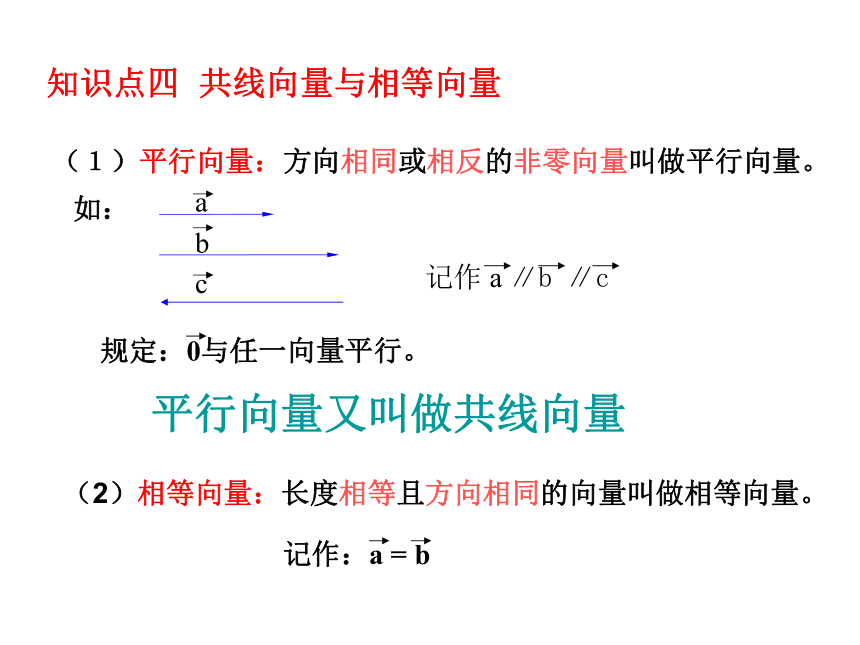
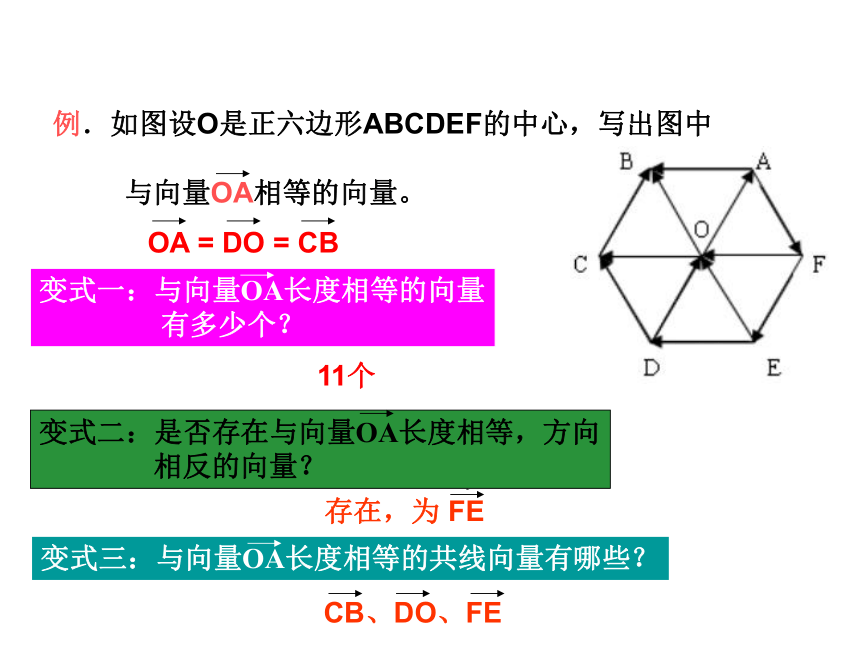
3.有向线段:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向。具有方向的线段叫做有向线段。有向线段的三个要素:起点、方向、长度A(起点)B(终点)1、向量的几何表示:用有向线段表示。知识点二 向量的表示知识点三 向量的长(或模)1.温度含零上和零下温度,所以温度是向量( ) 2.向量的模是一个正实数。( )注:向量不能比较大小 平行向量又叫做共线向量知识点四 共线向量与相等向量11个习题讲解 1.判断下列命题是否正确,若不正确,请简述理由.
?
①向量 与 是共线向量,则A、B、C、D 四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量(长度相同,方向相反的向量)不相等;
?
④共线的向量,若起点不同,则终点一定不同。2.下面几个命题: C A.0 B. 1 C. 2 D. 3 其中正确的个数是( )
习题讲解
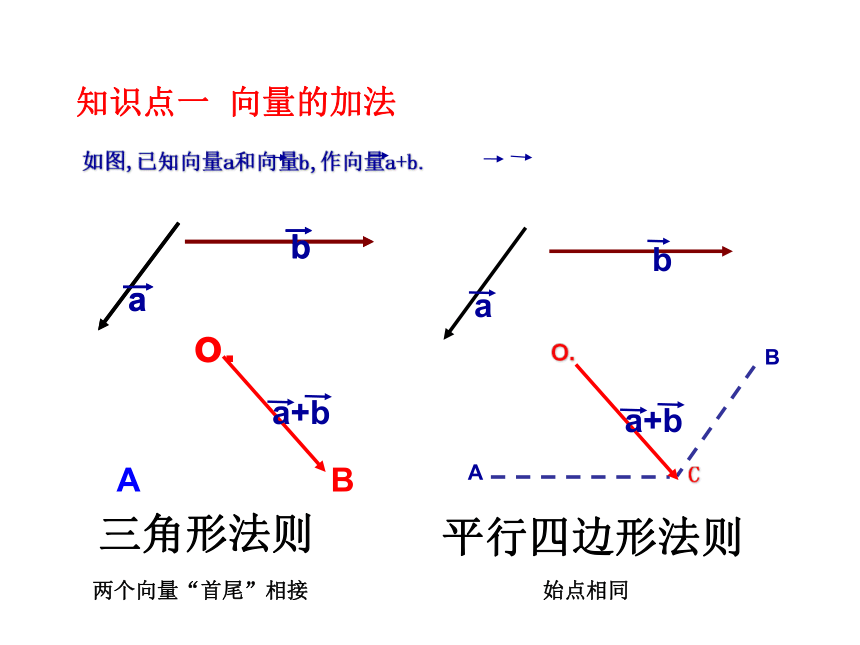
平面向量的线性运算知识点一 向量的加法BAo.O.AB
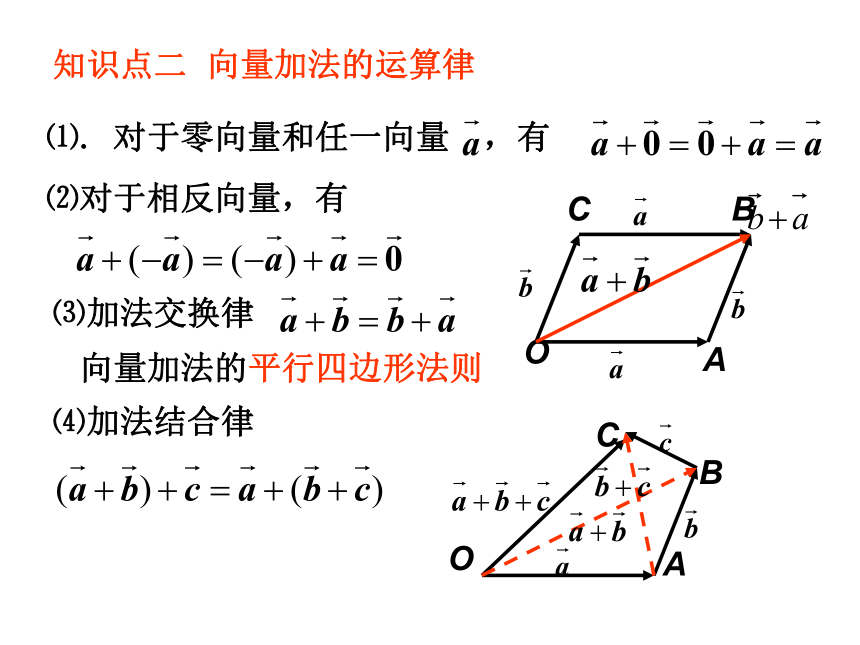
三角形法则平行四边形法则两个向量“首尾”相接始点相同知识点二 向量加法的运算律⑴. 对于零向量和任一向量 ,有⑵对于相反向量,有⑶加法交换律⑷加法结合律OABC向量加法的平行四边形法则 OABC知识点三 相反向量1.定义
与向量 方向相反长度相等的向量叫做a的相反向量,记作 。
2.性质
(1)
(2)若 互为相反向量,则
(3)零向量的相反向量仍是零向量。知识点四 向量的减法o.BAo.BA ,即减去一个向量相当于加上这个向量的相反向量。知识点五 向量加减法的三角形性质知识点六 向量的数乘实数 与向量 的积是个向量,这种运算叫做向量的数乘,记作 。当 >0时, 与 的方向相同;
当 <0时, 与 的方向相反;
当 =0时, =0知识点七 向量数乘的运算律结合律第一分配律第二分配律a∥ba=λb (λ∈R且b≠0)向量表示:知识点八 向量共线定理向量b与非零向量a共线的充分必要条件是有且只有一个实数λ,使得b=λa .1、填空题:90°2、判断题:
(1)相反向量就是方向相反的向量
(2)
(3)
(4) 在△ABC中,必有
(5)若 ,
则A、B、C三点必是一个三角形的三个顶点。( 错 )(对 )(错)(错)(对 ) 例1:根据条件判断下列四边形的形状平行四边形ABCD梯形ABCD 例2、 如图,在 中,延长BA到C,使AC=BA,在OB上取
点D,使BD= OB.DC与OA交于E,设 请用
. 分析: 解题的关键是建立
的联系,为此需要利用向量的加、减法数乘运算。 解:因为A是BC的中点,所以 例3、如图,设?ABCD一边AB的四等分点中最靠近B的一点为E,对角线BD的五等分点中靠近B的一点为F,求证:E、F、C三点在一条直线上.图1跟踪训练:1、有一边长为1的正方形ABCD,设 求: 2、已知A、B、C是不共线的三点,O是
△ABC内的一点,若 = 0,
则O 是△ABC的——————
(填内心、重心、垂心、外心等).1.外心:三角形三条垂直平分线的交点2.内心:三角形三条角平分线的交点3.垂心:三角形三条高线的交点4. 重心:三角形三条中线的交点课下作业:C.A.B.2.设 是非零向量, 是非零实数,下列结论正确的是( ).D.1.下列四个说法正确的个数有( ).B.2个A.1个C.3个D.4个????BC5D4.已知 表示向东走5 km, 表示向北走 5km,则 表示______________________ 向北偏东60?方向走10km5.在矩形ABCD中, , 。则向量 的长度等于 ( )A7.如图D、E、F分别为△ABC的边AB、BC、CA的中点,则下列等式正确的是 ( )A.B.C.D. DABCDEF8. , , 为非零向量,且 平分 与 的夹角,则……………………( )B 平面向量的基本定理及坐标表示 定理:如果e1,e2是同一平面内的两个 向量,那么对于这一平面内的任意向量a, 一对实数λ1,λ2,使a=__________.
其中,不共线的向量e1,e2叫做表示这一平面内所有向量的一组______.
一个平面向量用一组基底e1,e2表示成a=λ1e1+λ2e2的形式,称为向量的分解。不共线有且只有基底λ1e1+λ2e2知识点一 平面向量基本定理知识点二 两向量的夹角把一个向量分解为两个互相垂直的向量,叫做把
向量正交分解。在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i,j作为基底,对于平面内的一个向量a,有且只有一对实数x,y,使a=xi+yj,把有序数对 叫做向量a的坐标,记作a= ,其中 叫做a在x轴上的坐标, 叫做a在y轴上的坐标.(x,y)(x,y)xy知识点三 平面向量的坐标表示(2)两向量相等的充要条件是它们的坐标相等,即(3)以坐标原点O为起点的向量坐标就是该向量的终点坐标,
如设 ,则向量 的坐标就是点A的坐标 ,
反之亦然。(x1+x2,y1+y2) (x1-x2,y1-y2) (x2-x1,y2-y1) x1y2-x2y1=0 答案: D 答案: B 答案: A
答案: ①答案: 2n-m 答案: -1 答案: C答案: D 平面向量的数量积知识点一 平面向量的数量积
已知两个非零向量a和b,它们的夹角为θ,则数量
叫做a与b的数量积(或内积),记作 .
规定:零向量与任一向量的数量积为 .
两个非零向量a与b垂直的充要条件是 ,两非零向量a与b平行的充要条件是 .|a|·|b|cos θa·b=|a||b|·cos θ0a·b=0a·b=±|a||b|知识点二 平面向量数量积的几何意义
数量积a·b等于a的长度|a|与b在a方向上的投影
的乘积.
知识点三 平面向量数量积的性质
(1)e·a=a·e= ;
(2)非零向量a,b,a⊥b? ;
(3)当a与b同向时,a·b= ;
当a与b反向时,a·b= ,
a·a= =______,|a|= ;
(4)cos θ= ;
(5)|a·b| |a||b|. |b|cosθ|a|cos θa·b=0|a||b|-|a||b|a2≤ (1)a·b= (交换律);
(2)( a)·b= = ( 为实数);
(3)(a±b)·c= =__________.
(4)(a+b)·(a-b)=a2-b2;(a±b)2=a2±2a·b+b2
=b·a(a·b)a· ba·c±b·c知识点四 平面向量数量积的运算律c·(a±b)知识点五 平面向量数量积的坐标表示
设向量a=(x1,y1),b=(x2,y2),则 a·b= ,由此得到
(1)若a=(x,y),则|a|2= 或|a| .
(2)设A(x1,y1),B(x2,y2),则A、B两点间的距离|AB|=|AB|= .
(3)设a=(x1,y1),b=(x2,y2),
则a⊥b? .
a∥b _____________________.x1x2+y1y2x2+y2x1x2+y1y2=0x1y2-x2y1=0知识点六 两向量夹角的余弦公式设a、b是非零向量,a=(x1,y1),b=(x2,y2),θ是a与b的夹角,则有2.若|a|=2cos 15°,|b|=4sin 15°,a,b的夹角为30°,则a·b等于 ( )
A. B. C. D.
练习1
1.已知a=(2,3),b=(-4,7),则a在b上的投影为( )
A. B. C. D.
4.如图,在边长为 1 的正六边形 ABCDEF 中,下列向量的数量积中最大的是( )
例1、已知向量a=(cos x,sin x),
b=(cos ,-sin ),且x∈[ ].
(1)求a·b及|a+b|;
(2)若f(x)=a·b-|a+b|,求f(x)的最大值和最小值.
题型一 平面向量的数量积(1)已知O是△ABC内部一点, =0,
且∠BAC=30°,则△AOB的面积为
A.2 B.1 C. D.
(2)已知|a|=1,|b|=6,a·(b-a)=2,则向量a与b的夹角是
A. B. C. D.题型二 利用平面向量的数量积解决垂直问题
例2、已知向量a=(cos(-θ),sin(-θ)),b=
(1)求证:a⊥b;
(2)若存在不等于0的实数k和t,使x=a+(t2+3)b,
y=-ka+tb,满足x⊥y,试求此时 的最小值.
已知平面向量a=(- , ),b=(- , -1).
(1)证明:a⊥b;
(2)若存在不同时为零的实数k、t,使x=a+(t2- 2)b,
y=-ka+t2b,且x⊥y,试把k表示为t的函数.
题型三 向量的夹角及向量模的问题
例3、已知|a|=1,a·b= ,(a-b)·(a+b)= ,
求:(1)a与b的夹角;
(2)a-b与a+b的夹角的余弦值.
2、已知|a|=4,|b|=8,a与b的夹角是120°.
(1)计算:①|a+b|;②|4a-2b|;
(2)当k为何值时,(a+2b)⊥(ka-b)?
1.已知点A(1,0),B(0,1),C(2sinθ,cosθ).
(1)若| |=| |,求tanθ的值;
(2)若( )· =1,其中O为坐标原点,求sin 2θ的值.
2.在三角形ABC中,角A、B、C所对的边分别为a、
b、c,且2sin2 +cos 2C=1.
(1)求角C的大小;
(2)若向量m=(3a,-b),向量n=(a,- ),m⊥n,(m+n)·(-m+n)=-16.求a、b、c的值.
大小、方向。
2.数量:只有大小、没有方向的量
3.有向线段:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向。具有方向的线段叫做有向线段。有向线段的三个要素:起点、方向、长度A(起点)B(终点)1、向量的几何表示:用有向线段表示。知识点二 向量的表示知识点三 向量的长(或模)1.温度含零上和零下温度,所以温度是向量( ) 2.向量的模是一个正实数。( )注:向量不能比较大小 平行向量又叫做共线向量知识点四 共线向量与相等向量11个习题讲解 1.判断下列命题是否正确,若不正确,请简述理由.
?
①向量 与 是共线向量,则A、B、C、D 四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量(长度相同,方向相反的向量)不相等;
?
④共线的向量,若起点不同,则终点一定不同。2.下面几个命题: C A.0 B. 1 C. 2 D. 3 其中正确的个数是( )
习题讲解
平面向量的线性运算知识点一 向量的加法BAo.O.AB
三角形法则平行四边形法则两个向量“首尾”相接始点相同知识点二 向量加法的运算律⑴. 对于零向量和任一向量 ,有⑵对于相反向量,有⑶加法交换律⑷加法结合律OABC向量加法的平行四边形法则 OABC知识点三 相反向量1.定义
与向量 方向相反长度相等的向量叫做a的相反向量,记作 。
2.性质
(1)
(2)若 互为相反向量,则
(3)零向量的相反向量仍是零向量。知识点四 向量的减法o.BAo.BA ,即减去一个向量相当于加上这个向量的相反向量。知识点五 向量加减法的三角形性质知识点六 向量的数乘实数 与向量 的积是个向量,这种运算叫做向量的数乘,记作 。当 >0时, 与 的方向相同;
当 <0时, 与 的方向相反;
当 =0时, =0知识点七 向量数乘的运算律结合律第一分配律第二分配律a∥ba=λb (λ∈R且b≠0)向量表示:知识点八 向量共线定理向量b与非零向量a共线的充分必要条件是有且只有一个实数λ,使得b=λa .1、填空题:90°2、判断题:
(1)相反向量就是方向相反的向量
(2)
(3)
(4) 在△ABC中,必有
(5)若 ,
则A、B、C三点必是一个三角形的三个顶点。( 错 )(对 )(错)(错)(对 ) 例1:根据条件判断下列四边形的形状平行四边形ABCD梯形ABCD 例2、 如图,在 中,延长BA到C,使AC=BA,在OB上取
点D,使BD= OB.DC与OA交于E,设 请用
. 分析: 解题的关键是建立
的联系,为此需要利用向量的加、减法数乘运算。 解:因为A是BC的中点,所以 例3、如图,设?ABCD一边AB的四等分点中最靠近B的一点为E,对角线BD的五等分点中靠近B的一点为F,求证:E、F、C三点在一条直线上.图1跟踪训练:1、有一边长为1的正方形ABCD,设 求: 2、已知A、B、C是不共线的三点,O是
△ABC内的一点,若 = 0,
则O 是△ABC的——————
(填内心、重心、垂心、外心等).1.外心:三角形三条垂直平分线的交点2.内心:三角形三条角平分线的交点3.垂心:三角形三条高线的交点4. 重心:三角形三条中线的交点课下作业:C.A.B.2.设 是非零向量, 是非零实数,下列结论正确的是( ).D.1.下列四个说法正确的个数有( ).B.2个A.1个C.3个D.4个????BC5D4.已知 表示向东走5 km, 表示向北走 5km,则 表示______________________ 向北偏东60?方向走10km5.在矩形ABCD中, , 。则向量 的长度等于 ( )A7.如图D、E、F分别为△ABC的边AB、BC、CA的中点,则下列等式正确的是 ( )A.B.C.D. DABCDEF8. , , 为非零向量,且 平分 与 的夹角,则……………………( )B 平面向量的基本定理及坐标表示 定理:如果e1,e2是同一平面内的两个 向量,那么对于这一平面内的任意向量a, 一对实数λ1,λ2,使a=__________.
其中,不共线的向量e1,e2叫做表示这一平面内所有向量的一组______.
一个平面向量用一组基底e1,e2表示成a=λ1e1+λ2e2的形式,称为向量的分解。不共线有且只有基底λ1e1+λ2e2知识点一 平面向量基本定理知识点二 两向量的夹角把一个向量分解为两个互相垂直的向量,叫做把
向量正交分解。在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i,j作为基底,对于平面内的一个向量a,有且只有一对实数x,y,使a=xi+yj,把有序数对 叫做向量a的坐标,记作a= ,其中 叫做a在x轴上的坐标, 叫做a在y轴上的坐标.(x,y)(x,y)xy知识点三 平面向量的坐标表示(2)两向量相等的充要条件是它们的坐标相等,即(3)以坐标原点O为起点的向量坐标就是该向量的终点坐标,
如设 ,则向量 的坐标就是点A的坐标 ,
反之亦然。(x1+x2,y1+y2) (x1-x2,y1-y2) (x2-x1,y2-y1) x1y2-x2y1=0 答案: D 答案: B 答案: A
答案: ①答案: 2n-m 答案: -1 答案: C答案: D 平面向量的数量积知识点一 平面向量的数量积
已知两个非零向量a和b,它们的夹角为θ,则数量
叫做a与b的数量积(或内积),记作 .
规定:零向量与任一向量的数量积为 .
两个非零向量a与b垂直的充要条件是 ,两非零向量a与b平行的充要条件是 .|a|·|b|cos θa·b=|a||b|·cos θ0a·b=0a·b=±|a||b|知识点二 平面向量数量积的几何意义
数量积a·b等于a的长度|a|与b在a方向上的投影
的乘积.
知识点三 平面向量数量积的性质
(1)e·a=a·e= ;
(2)非零向量a,b,a⊥b? ;
(3)当a与b同向时,a·b= ;
当a与b反向时,a·b= ,
a·a= =______,|a|= ;
(4)cos θ= ;
(5)|a·b| |a||b|. |b|cosθ|a|cos θa·b=0|a||b|-|a||b|a2≤ (1)a·b= (交换律);
(2)( a)·b= = ( 为实数);
(3)(a±b)·c= =__________.
(4)(a+b)·(a-b)=a2-b2;(a±b)2=a2±2a·b+b2
=b·a(a·b)a· ba·c±b·c知识点四 平面向量数量积的运算律c·(a±b)知识点五 平面向量数量积的坐标表示
设向量a=(x1,y1),b=(x2,y2),则 a·b= ,由此得到
(1)若a=(x,y),则|a|2= 或|a| .
(2)设A(x1,y1),B(x2,y2),则A、B两点间的距离|AB|=|AB|= .
(3)设a=(x1,y1),b=(x2,y2),
则a⊥b? .
a∥b _____________________.x1x2+y1y2x2+y2x1x2+y1y2=0x1y2-x2y1=0知识点六 两向量夹角的余弦公式设a、b是非零向量,a=(x1,y1),b=(x2,y2),θ是a与b的夹角,则有2.若|a|=2cos 15°,|b|=4sin 15°,a,b的夹角为30°,则a·b等于 ( )
A. B. C. D.
练习1
1.已知a=(2,3),b=(-4,7),则a在b上的投影为( )
A. B. C. D.
4.如图,在边长为 1 的正六边形 ABCDEF 中,下列向量的数量积中最大的是( )
例1、已知向量a=(cos x,sin x),
b=(cos ,-sin ),且x∈[ ].
(1)求a·b及|a+b|;
(2)若f(x)=a·b-|a+b|,求f(x)的最大值和最小值.
题型一 平面向量的数量积(1)已知O是△ABC内部一点, =0,
且∠BAC=30°,则△AOB的面积为
A.2 B.1 C. D.
(2)已知|a|=1,|b|=6,a·(b-a)=2,则向量a与b的夹角是
A. B. C. D.题型二 利用平面向量的数量积解决垂直问题
例2、已知向量a=(cos(-θ),sin(-θ)),b=
(1)求证:a⊥b;
(2)若存在不等于0的实数k和t,使x=a+(t2+3)b,
y=-ka+tb,满足x⊥y,试求此时 的最小值.
已知平面向量a=(- , ),b=(- , -1).
(1)证明:a⊥b;
(2)若存在不同时为零的实数k、t,使x=a+(t2- 2)b,
y=-ka+t2b,且x⊥y,试把k表示为t的函数.
题型三 向量的夹角及向量模的问题
例3、已知|a|=1,a·b= ,(a-b)·(a+b)= ,
求:(1)a与b的夹角;
(2)a-b与a+b的夹角的余弦值.
2、已知|a|=4,|b|=8,a与b的夹角是120°.
(1)计算:①|a+b|;②|4a-2b|;
(2)当k为何值时,(a+2b)⊥(ka-b)?
1.已知点A(1,0),B(0,1),C(2sinθ,cosθ).
(1)若| |=| |,求tanθ的值;
(2)若( )· =1,其中O为坐标原点,求sin 2θ的值.
2.在三角形ABC中,角A、B、C所对的边分别为a、
b、c,且2sin2 +cos 2C=1.
(1)求角C的大小;
(2)若向量m=(3a,-b),向量n=(a,- ),m⊥n,(m+n)·(-m+n)=-16.求a、b、c的值.
