旋转对称图形
图片预览





文档简介
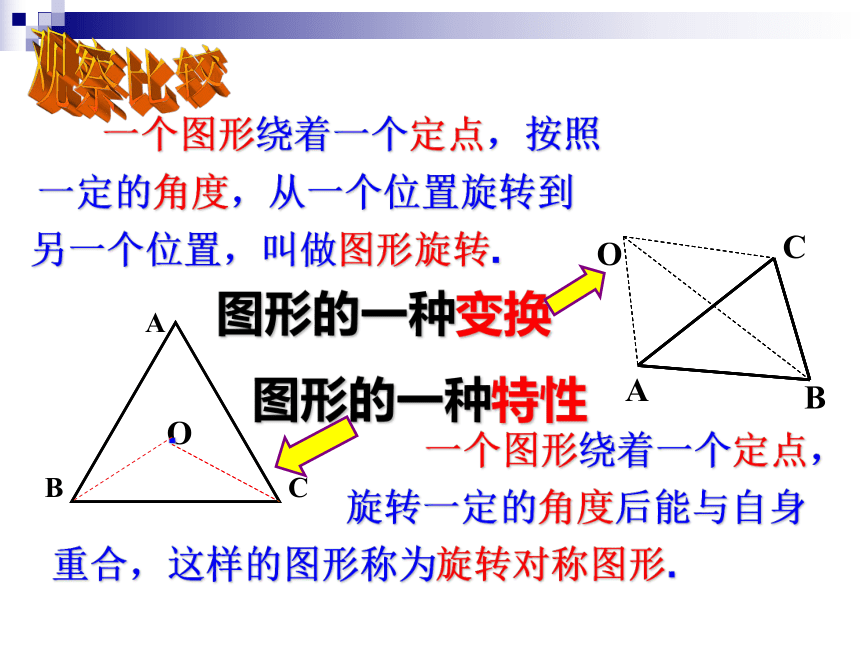
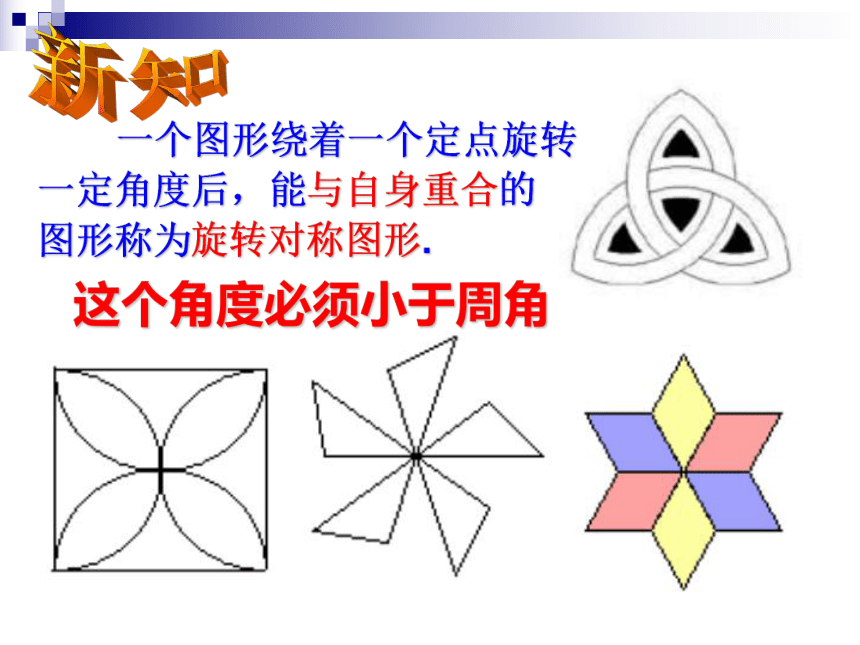
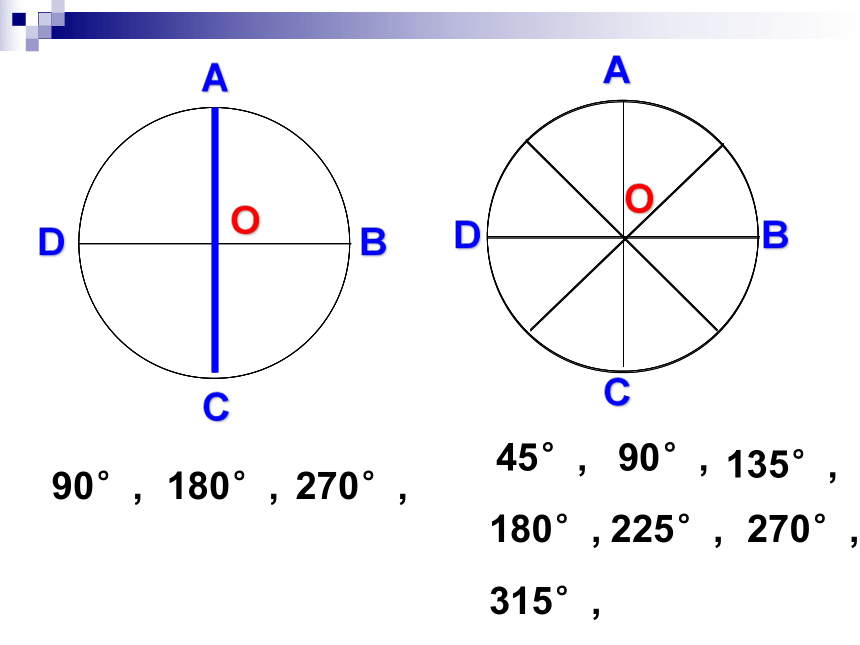
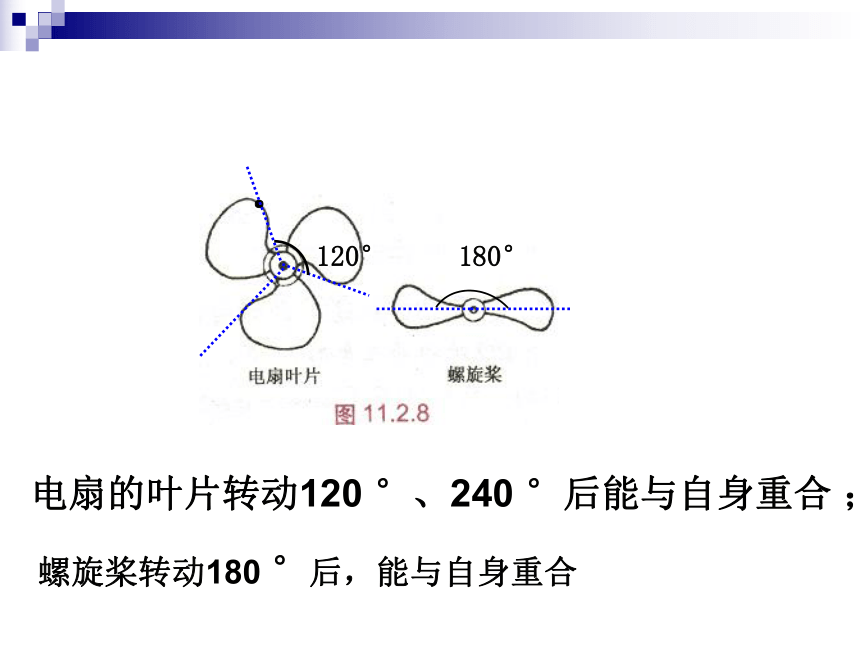
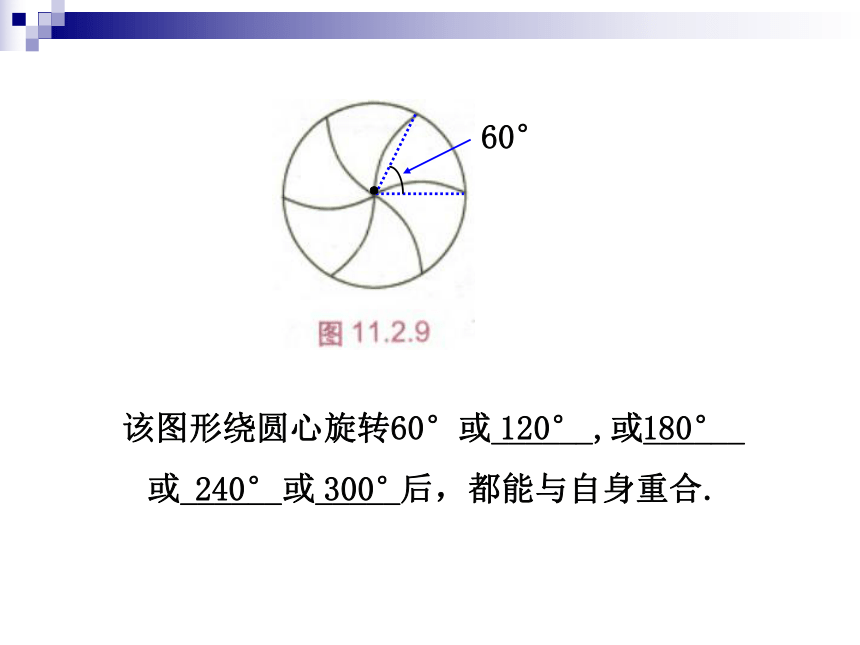
课件33张PPT。旋转对称图形南侨中学 洪丽影轴对称图形旋转对称图形知识回顾⑴旋转的概念:在平面内,将一个图形绕着一个定点沿某个方向转动一个角度的运动叫做旋转.⑵旋转的特征:①旋转不改变图形大小和形状;②旋转图形的对应线段相等, 对应角相等;③对应点到旋转中心的距离相等;④每一点都绕旋转中心按同一方向旋转同样大小的角度, 即对应点的连线的角相等.BACO一个图形绕着一个定点,按照一定的角度,从一个位置旋转到另一个位置,叫做图形旋转.ABC一个图形绕着一个定点,旋转一定的角度后能与自身重合,这样的图形称为旋转对称图形.观察比较图形的一种变换图形的一种特性O·一个图形绕着一个定点旋转新知一定角度后,能与自身重合的图形称为旋转对称图形.这个角度必须小于周角ABCDO90°,180°,270°,ADCBO45°,90°,135°,180°,225°,270°,315°,螺旋桨转动180 °后,能与自身重合 ·180°120°旋转对称图形电扇的叶片转动120 °、240 °后能与自身重合 ;60°旋转对称图形该图形绕圆心旋转60°或______,或______
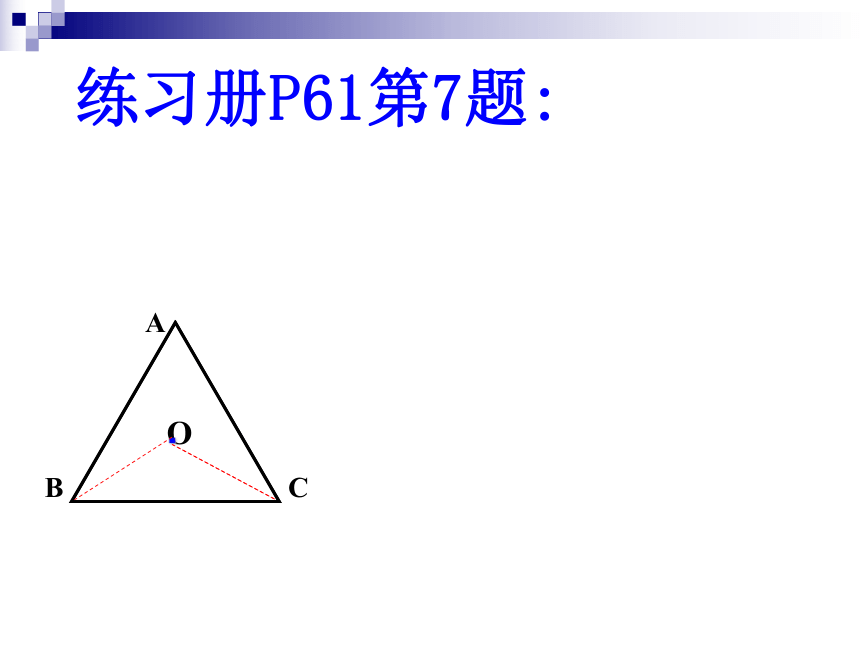
或______或_____后,都能与自身重合.120°180°240°300°·旋转对称图形图形绕着某一定点旋转一定的角度后能与自身重合旋转对称图形____例如:线段、等边三角形、平行四边形、圆都是旋转对称图形.ABCO·练习册P61第7题:如图,(1)它是不是旋转对称图形?
(2)旋转中心在何处?
(3)该图形需要旋转多少度后,
能与自身重合?
(4)该图形是轴对称图形吗?(1)这个图形是旋转对称图形;
(2)如图所示,点O为旋转中心;
(3)该图形需要旋转90度后,能与自身重合;
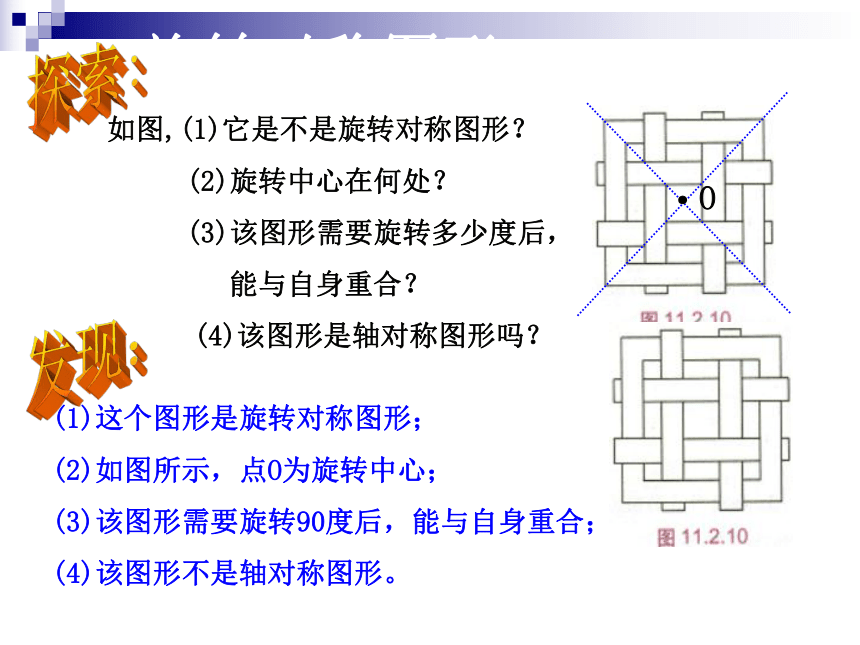
(4)该图形不是轴对称图形。旋转对称图形·O发现:探索:如图,(1)它是不是旋转对称图形?
(2)旋转中心在何处?
(3)该图形需要旋转多少度后,
能与自身重合?
(4)该图形是轴对称图形吗?(1)这个图形是旋转对称图形;
(2)如图所示,点O为旋转中心;
(3)该图形需要旋转180度后,能与自身重合;
(4)该图形是轴对称图形,有两条对称轴.(如图)旋转对称图形·发现:探索:·O旋转对称图形P69(做一做)A″A′C′B′C″B″△ABC 旋转后得到△A″B″C″.A平移与轴对称BCl1┗A′B′C′甲乙图形甲与图形乙称之为关于直线l1轴对称l2A′′′B′C′′关于两条平行直线连续2次轴对称可以看作是一次平移.例4:如图,在纸上画出△ABC和两条不平行的对称轴m、n,画出△ABC关于直线m对称的△A’B’C’,再画出△A’B’C’关于直线n对称的△A”B”C”,再观察△ABC与△A”B”C”这两
个图形的位置关系发生了什么变化?解:如图,△A’B’C’是△ABC关于直线m的对称图形,△A”B”C”是△A’B’C’关于直线n对称的图形。△ABC与△A”B”C”相当于作了一次旋转变换,其旋转中心是直线m、n的交点。A’B’C’ACBA”B”C”mn2.答:图形中有4匹马.绕矩形两条对角线的交点旋转180°,两匹马能够分别与另两匹马重合,这个图形是中心对称图形.旋转对称图形·练习:课本70页第2题3.答(1)将图形绕圆心旋转60°、 120°、180°、 240°、 300°后都能与自身重合.(2)将图形绕中心旋转90°、 180°、270°后都能与自身重合.旋转对称图形练习:课本70页第3题1.答:将如图所示的五角星绕中心旋转72°、 144°、216°、 288°后都能与自身重合.旋转对称图形72°练习:课本70页第2题4.答:旋转120°、 240°后都能与自身重合.旋转对称图形练习:课本71页第4题5.答:将如图所示图形绕中心旋转40°、 80°、120°、 160° 、200°、 240°、 280°、 320°后都能与自身重合.40°旋转对称图形练习:课本71页第5题选择题 ☆正三角形、正方形、等腰三角形、线段中,不是旋转对称图形的是( )
(A)正三角形.
(B)正方形.
(C)等腰三角形.
(D)线段.C旋转对称图形 3.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它可以由其中一瓣经过4次旋转而得到. 它是旋转对称图形吗? 若是,其旋转角是多少度?例练1. 试确定下列旋转图形的旋转中心和旋转角度.例练2.OA例练3. 下列各图形是不是旋转对称图形?如果是,
请找出旋转中心在何处。旋转角度至少是多少
度?这些图形是轴对称图形吗? 120° ┍ 90° 60° 正三角形是旋转对
称图形, 它的旋转中
心是两条高线的交
点, 旋转角度是120°
它也是轴对称图形.正方形是旋转对称
图形, 它的旋转中心
是两条对角线的交
点, 旋转角度是90°
它也是轴对称图形.正六边形是旋转对称
图形, 它的旋转中心
是两条对角线的交
点, 旋转角度是60°
它也是轴对称图形. 观察下图,判断它是不是旋转对称图形?如果是,请找出旋转中心在何处,旋转角度是多少?另外该图形是轴对称图形吗? 例练4.解:这个图形是旋转对称图形,旋转中心是外框正方形对角线的交点(如图中的点O),旋转角度是90°,但它不是轴对称图形.例练5. 试确定图形的旋转中心,并指出这一图形是由哪个基本图形旋转多少度、旋转几次生成的? 解:旋转中心是十字形的交点O,基本图形O · 如图所示,分别旋转了90°、180°、270°三次生成的。 例练6. 请利用如图所示的图案,通过旋转变换,设计出美丽的图案。 课堂小结⑴绕着某一点转动一定角度后,能与自身重合的图形称为旋转对称图形, 其中这一点就是旋转中心,这个角度的最小值就是旋转角. ⑵如果一个图形既是旋转对称图形,又是轴对称图形,那么它的旋转中心就是对称轴的交点. ⑶正n边形既是旋转对称图形,又是轴对称图形,所以它的旋转中心就是对称轴的交点,并且旋转角度就等于360°除于n所得的商. 探索 ⑴△ABC是△DEF旋转得到的,你能找到它的旋转中心吗?若能请画出来. O·ABCDEF ⑵如图所示两个圆,其中圆O2是由圆O1旋转得到的,请问你能否找到它的旋转中心?有多少个? 探索 ⑶如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF,请找出经过△ABC旋转能够得到的三角形 . 探索 ⑷如图,画△ABC关于直线a,b 连续两次对称的图形, 并观察与原图形的关系. abOABC再 见
或______或_____后,都能与自身重合.120°180°240°300°·旋转对称图形图形绕着某一定点旋转一定的角度后能与自身重合旋转对称图形____例如:线段、等边三角形、平行四边形、圆都是旋转对称图形.ABCO·练习册P61第7题:如图,(1)它是不是旋转对称图形?
(2)旋转中心在何处?
(3)该图形需要旋转多少度后,
能与自身重合?
(4)该图形是轴对称图形吗?(1)这个图形是旋转对称图形;
(2)如图所示,点O为旋转中心;
(3)该图形需要旋转90度后,能与自身重合;
(4)该图形不是轴对称图形。旋转对称图形·O发现:探索:如图,(1)它是不是旋转对称图形?
(2)旋转中心在何处?
(3)该图形需要旋转多少度后,
能与自身重合?
(4)该图形是轴对称图形吗?(1)这个图形是旋转对称图形;
(2)如图所示,点O为旋转中心;
(3)该图形需要旋转180度后,能与自身重合;
(4)该图形是轴对称图形,有两条对称轴.(如图)旋转对称图形·发现:探索:·O旋转对称图形P69(做一做)A″A′C′B′C″B″△ABC 旋转后得到△A″B″C″.A平移与轴对称BCl1┗A′B′C′甲乙图形甲与图形乙称之为关于直线l1轴对称l2A′′′B′C′′关于两条平行直线连续2次轴对称可以看作是一次平移.例4:如图,在纸上画出△ABC和两条不平行的对称轴m、n,画出△ABC关于直线m对称的△A’B’C’,再画出△A’B’C’关于直线n对称的△A”B”C”,再观察△ABC与△A”B”C”这两
个图形的位置关系发生了什么变化?解:如图,△A’B’C’是△ABC关于直线m的对称图形,△A”B”C”是△A’B’C’关于直线n对称的图形。△ABC与△A”B”C”相当于作了一次旋转变换,其旋转中心是直线m、n的交点。A’B’C’ACBA”B”C”mn2.答:图形中有4匹马.绕矩形两条对角线的交点旋转180°,两匹马能够分别与另两匹马重合,这个图形是中心对称图形.旋转对称图形·练习:课本70页第2题3.答(1)将图形绕圆心旋转60°、 120°、180°、 240°、 300°后都能与自身重合.(2)将图形绕中心旋转90°、 180°、270°后都能与自身重合.旋转对称图形练习:课本70页第3题1.答:将如图所示的五角星绕中心旋转72°、 144°、216°、 288°后都能与自身重合.旋转对称图形72°练习:课本70页第2题4.答:旋转120°、 240°后都能与自身重合.旋转对称图形练习:课本71页第4题5.答:将如图所示图形绕中心旋转40°、 80°、120°、 160° 、200°、 240°、 280°、 320°后都能与自身重合.40°旋转对称图形练习:课本71页第5题选择题 ☆正三角形、正方形、等腰三角形、线段中,不是旋转对称图形的是( )
(A)正三角形.
(B)正方形.
(C)等腰三角形.
(D)线段.C旋转对称图形 3.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它可以由其中一瓣经过4次旋转而得到. 它是旋转对称图形吗? 若是,其旋转角是多少度?例练1. 试确定下列旋转图形的旋转中心和旋转角度.例练2.OA例练3. 下列各图形是不是旋转对称图形?如果是,
请找出旋转中心在何处。旋转角度至少是多少
度?这些图形是轴对称图形吗? 120° ┍ 90° 60° 正三角形是旋转对
称图形, 它的旋转中
心是两条高线的交
点, 旋转角度是120°
它也是轴对称图形.正方形是旋转对称
图形, 它的旋转中心
是两条对角线的交
点, 旋转角度是90°
它也是轴对称图形.正六边形是旋转对称
图形, 它的旋转中心
是两条对角线的交
点, 旋转角度是60°
它也是轴对称图形. 观察下图,判断它是不是旋转对称图形?如果是,请找出旋转中心在何处,旋转角度是多少?另外该图形是轴对称图形吗? 例练4.解:这个图形是旋转对称图形,旋转中心是外框正方形对角线的交点(如图中的点O),旋转角度是90°,但它不是轴对称图形.例练5. 试确定图形的旋转中心,并指出这一图形是由哪个基本图形旋转多少度、旋转几次生成的? 解:旋转中心是十字形的交点O,基本图形O · 如图所示,分别旋转了90°、180°、270°三次生成的。 例练6. 请利用如图所示的图案,通过旋转变换,设计出美丽的图案。 课堂小结⑴绕着某一点转动一定角度后,能与自身重合的图形称为旋转对称图形, 其中这一点就是旋转中心,这个角度的最小值就是旋转角. ⑵如果一个图形既是旋转对称图形,又是轴对称图形,那么它的旋转中心就是对称轴的交点. ⑶正n边形既是旋转对称图形,又是轴对称图形,所以它的旋转中心就是对称轴的交点,并且旋转角度就等于360°除于n所得的商. 探索 ⑴△ABC是△DEF旋转得到的,你能找到它的旋转中心吗?若能请画出来. O·ABCDEF ⑵如图所示两个圆,其中圆O2是由圆O1旋转得到的,请问你能否找到它的旋转中心?有多少个? 探索 ⑶如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形即△ABD、△BCE、△ACF,请找出经过△ABC旋转能够得到的三角形 . 探索 ⑷如图,画△ABC关于直线a,b 连续两次对称的图形, 并观察与原图形的关系. abOABC再 见
