19-1-1变量与函数课件-人教版数学八年级下册(15张ppt)
文档属性
| 名称 | 19-1-1变量与函数课件-人教版数学八年级下册(15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
WS
19.1.1变量与函数
第一课时 变量与常量
学习目标:
1.了解变量与常量的意义;
2.体会运动变化过程中的数量变化.
学习重点:
了解变量与常量的意义,充分体会运动变化过程中量的变化.
学习难点:
掌握常量,变量的概念及它们之间的关系。
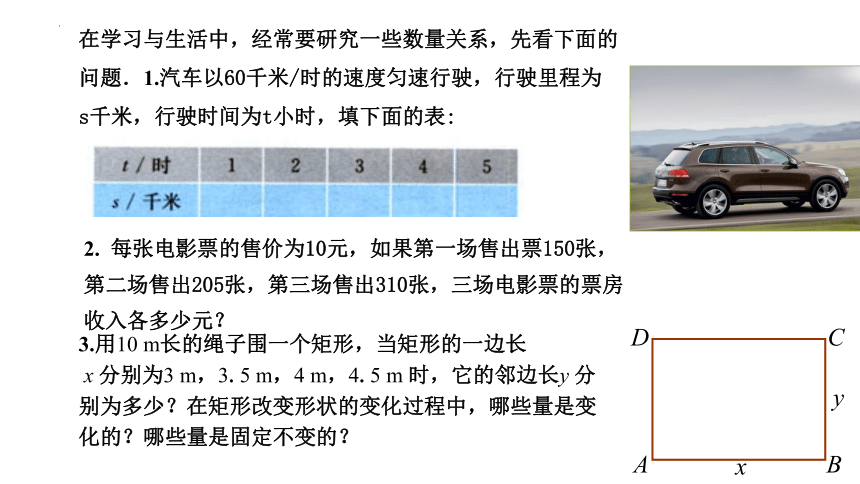
在学习与生活中,经常要研究一些数量关系,先看下面的问题.1.汽车以60千米/时的速度匀速行驶,行驶里程为
s千米,行驶时间为t小时,填下面的表:
2. 每张电影票的售价为10元,如果第一场售出票150张,
第二场售出205张,第三场售出310张,三场电影票的票房
收入各多少元?
3.用10 m长的绳子围一个矩形,当矩形的一边长
x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分
别为多少?在矩形改变形状的变化过程中,哪些量是变
化的?哪些量是固定不变的?
x
y
A
B
C
D
汽车以60千米/时的速度匀速行驶,行驶里程为
s千米,行驶时间为t小时,填下面的表:
请说明你的道理。
路程 = 速度×时间
试用含t的式子表示s。
s = 60t
60
120
180
240
300
小结:行驶路程随 时间 的变化而变化,关系式
s= 60t ,即s随 t 的变化而变化;
问题一
每张电影票的售价为10元,如果第一场售出票150张,
第二场售出205张,第三场售出310张,三场电影票的票房
收入各多少元?
第一场票房收入 = 10×150 = 1500 (元)
第二场票房收入 = 10×205 = 2050 (元)
第三场票房收入 = 10×310 = 3100 (元)
若设一场电影售出票x张,票房收入为y元,怎样用含x的式子表示y?
y = 10x
请说明道理:
票房收入= 售价×售票张数
小结:票房收入随售出的电影票数变化而
变化,即 y随 X 的变化而变化;
问题二
x
y
A
B
C
D
下面问题中变化的量和不变的量:
(4)用10 m长的绳子围一个矩形,当矩形的一边长
x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分
别为多少?在矩形改变形状的变化过程中,哪些量是变
化的?哪些量是固定不变的?
问题三
y=5-x
小结:矩形的邻边长度随矩形的一边长的变化而变化,即 y随 x 的变化而变化;
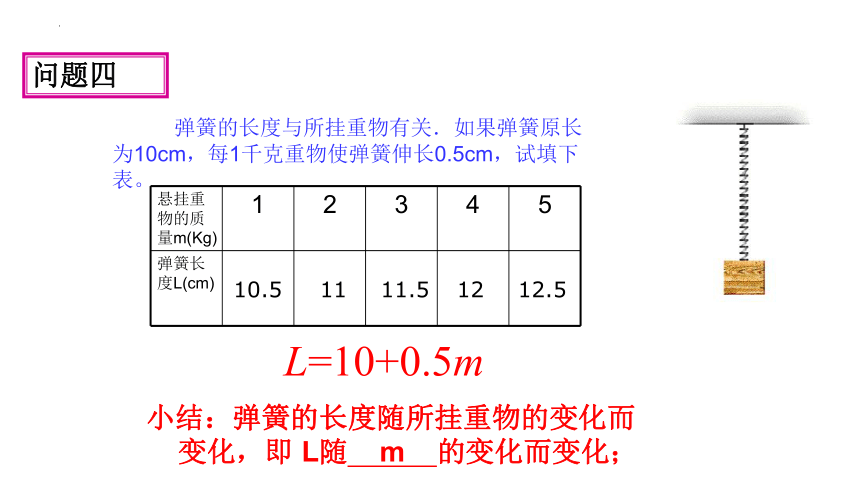
弹簧的长度与所挂重物有关.如果弹簧原长
为10cm,每1千克重物使弹簧伸长0.5cm,试填下
表。
L=10+0.5m
悬挂重物的质量m(Kg) 1 2 3 4 5
弹簧长度L(cm)
10.5
11
11.5
12
12.5
小结:弹簧的长度随所挂重物的变化而
变化,即 L随 m 的变化而变化;
问题四
(4)y=5-x
(3)L=10+0.5m
(2)y=10x
在一个变化过程中,数值发生变化的量为变量.
变量:
在一个变化过程中,数值始终不变的量为常量.
常量:
共同特征:
1.都有两个互相联系的变量.
2.当其中的一个变量取定一个值,另一个变量有唯一确定的值与其对应.
归纳
(1)S=60t
圆形水波慢慢地扩大,在这一过程中,当圆的半径r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别为多少?在这个过程中,哪些量是变化的?
巩固练习
指出下列变化过程中的变量和常量:
(1)汽油的价格是7.4元/升,加油 x L,车主加油
付油费 y 元;
(2)小明看一本200 页的小说,看完这本小说需要
t 天,平均每天所看的页数为 n;
(3)用长为40 cm 的绳子围矩形,围成的矩形一边
长为 x cm,其面积为 S cm2.
1.某位教师为学生购买数学辅导书,书的单价是4元,则
总金额y(元)与学生数n(个)的关系式是 .
其中的变量是 .常量是 .
2.计划购买50元的乒乓球,所能购买的总数n(个)与单价 a(元)的关系式为 .其中的变量是 _ ,
常量是 .
3.圆的周长公式 ,这里的变量是 ,常量是 .
y=4n
n和y
4
n=50/a
a和n
50
r和C
2π
收获乐园
1.本节课你学到了哪些知识?
2.本节课你存在哪些困惑?
数值不断
变化的量
变量
数值固定
不变的量
常量
课堂小结
教科书第71~72页.
课后作业
Thank you!
谢谢同学们的努力!
WS
19.1.1变量与函数
第一课时 变量与常量
学习目标:
1.了解变量与常量的意义;
2.体会运动变化过程中的数量变化.
学习重点:
了解变量与常量的意义,充分体会运动变化过程中量的变化.
学习难点:
掌握常量,变量的概念及它们之间的关系。
在学习与生活中,经常要研究一些数量关系,先看下面的问题.1.汽车以60千米/时的速度匀速行驶,行驶里程为
s千米,行驶时间为t小时,填下面的表:
2. 每张电影票的售价为10元,如果第一场售出票150张,
第二场售出205张,第三场售出310张,三场电影票的票房
收入各多少元?
3.用10 m长的绳子围一个矩形,当矩形的一边长
x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分
别为多少?在矩形改变形状的变化过程中,哪些量是变
化的?哪些量是固定不变的?
x
y
A
B
C
D
汽车以60千米/时的速度匀速行驶,行驶里程为
s千米,行驶时间为t小时,填下面的表:
请说明你的道理。
路程 = 速度×时间
试用含t的式子表示s。
s = 60t
60
120
180
240
300
小结:行驶路程随 时间 的变化而变化,关系式
s= 60t ,即s随 t 的变化而变化;
问题一
每张电影票的售价为10元,如果第一场售出票150张,
第二场售出205张,第三场售出310张,三场电影票的票房
收入各多少元?
第一场票房收入 = 10×150 = 1500 (元)
第二场票房收入 = 10×205 = 2050 (元)
第三场票房收入 = 10×310 = 3100 (元)
若设一场电影售出票x张,票房收入为y元,怎样用含x的式子表示y?
y = 10x
请说明道理:
票房收入= 售价×售票张数
小结:票房收入随售出的电影票数变化而
变化,即 y随 X 的变化而变化;
问题二
x
y
A
B
C
D
下面问题中变化的量和不变的量:
(4)用10 m长的绳子围一个矩形,当矩形的一边长
x 分别为3 m,3.5 m,4 m,4.5 m 时,它的邻边长y 分
别为多少?在矩形改变形状的变化过程中,哪些量是变
化的?哪些量是固定不变的?
问题三
y=5-x
小结:矩形的邻边长度随矩形的一边长的变化而变化,即 y随 x 的变化而变化;
弹簧的长度与所挂重物有关.如果弹簧原长
为10cm,每1千克重物使弹簧伸长0.5cm,试填下
表。
L=10+0.5m
悬挂重物的质量m(Kg) 1 2 3 4 5
弹簧长度L(cm)
10.5
11
11.5
12
12.5
小结:弹簧的长度随所挂重物的变化而
变化,即 L随 m 的变化而变化;
问题四
(4)y=5-x
(3)L=10+0.5m
(2)y=10x
在一个变化过程中,数值发生变化的量为变量.
变量:
在一个变化过程中,数值始终不变的量为常量.
常量:
共同特征:
1.都有两个互相联系的变量.
2.当其中的一个变量取定一个值,另一个变量有唯一确定的值与其对应.
归纳
(1)S=60t
圆形水波慢慢地扩大,在这一过程中,当圆的半径r 分别为10 cm,20 cm,30 cm 时,圆的面积S 分别为多少?在这个过程中,哪些量是变化的?
巩固练习
指出下列变化过程中的变量和常量:
(1)汽油的价格是7.4元/升,加油 x L,车主加油
付油费 y 元;
(2)小明看一本200 页的小说,看完这本小说需要
t 天,平均每天所看的页数为 n;
(3)用长为40 cm 的绳子围矩形,围成的矩形一边
长为 x cm,其面积为 S cm2.
1.某位教师为学生购买数学辅导书,书的单价是4元,则
总金额y(元)与学生数n(个)的关系式是 .
其中的变量是 .常量是 .
2.计划购买50元的乒乓球,所能购买的总数n(个)与单价 a(元)的关系式为 .其中的变量是 _ ,
常量是 .
3.圆的周长公式 ,这里的变量是 ,常量是 .
y=4n
n和y
4
n=50/a
a和n
50
r和C
2π
收获乐园
1.本节课你学到了哪些知识?
2.本节课你存在哪些困惑?
数值不断
变化的量
变量
数值固定
不变的量
常量
课堂小结
教科书第71~72页.
课后作业
Thank you!
谢谢同学们的努力!
