11.1同底数幂的乘法

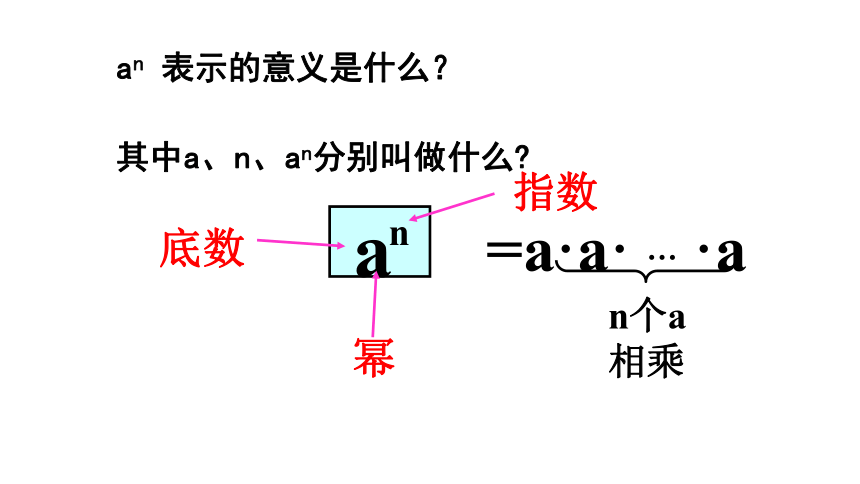
课件20张PPT。 11.1同底数幂的乘法 （1课时）广平中学 王远勇指数幂底数an 表示的意义是什么？
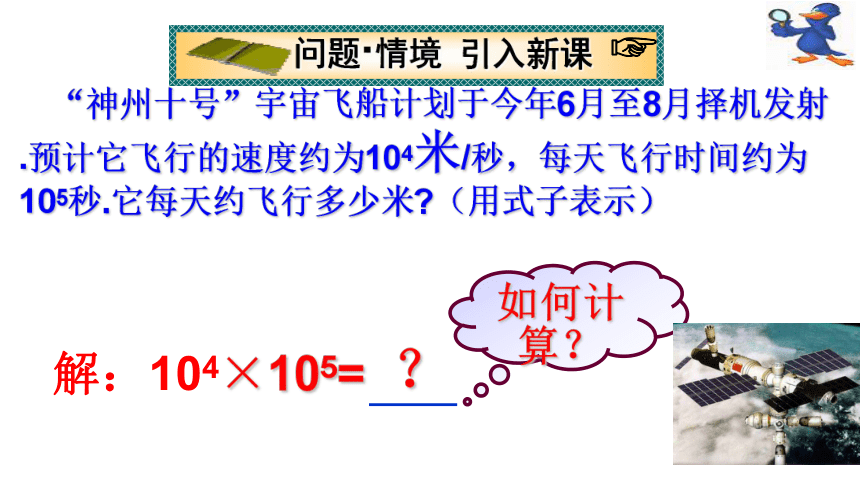
其中a、n、an分别叫做什么? 例题解析　“神州十号”宇宙飞船计划于今年6月至8月择机发射.预计它飞行的速度约为104米/秒，每天飞行时间约为 105秒.它每天约飞行多少米?（用式子表示）
问题·情境 引入新课 ?解：104×105= ？ 探究（一）根据乘方的意义试着解决下列问题
1、 = .
= = .
2、 = .
= = .
3、 = .
= .
= .
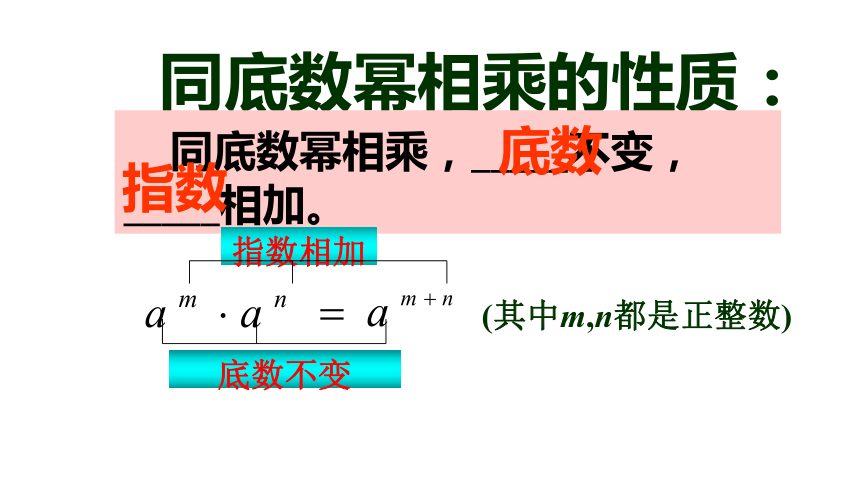
(10×10) ×(10×10×10）10×10×10×10×10(-2)(-2)(-2)(-2)(-2)(-2)(a·a·a)(a·a·a·a)a·a·a·a·a·a·a先试着自己解决，然后小组讨论。===探究（二）思考：观察上面3个等式，等式中各因数(式）的底数、指数与积中的底数、指数各有什么关系？底数相同，积的指数等于各个因数(式）指数的和。你能猜测并推导一下 am · an (m、n都是正整数)的结果吗？并试着用语言概括这一性质。 am · an =（aa…a）m个a（aa…a）n个a= aa…a= am+nam · an = (m、n都是正整数)探究（三）同底数幂相乘，底数不变，指数相加。(m+n)个a猜测：推导：am+n同底数幂相乘的性质： 同底数幂相乘，_____不变，_____相加。底数指数 (其中m,n都是正整数)（1）32×35 （2）(-5)3×(-5)5解：（1） 32×35
=32+5
=37（2）(-5)3×(-5)5
=(-5)3+5
=(-5)8
=58例1、计算： 练习一
1.???计算：( 710 )( a15 )（ x8 ）（ b6 ）（2） a7 ·a8（3） (-x)5 ·(-x)3 （4） b5 · b （1） 76×74（2） a7 ·a8（3） (-x)5 ·(-x)3 （4） b5 · b （1） 76×74例题讲解例2、计算 解：
你能根据这个特例总结出三个同底数幂相乘的法则吗？(m,n,p都是正整数)法2： am+n+p（1）22×24×25 （2）a6.a3.a2 解：（1）22×24×25=211
（2）a6.a3.a2 =a11计算：例2、计算：am · an = am+n (当m、n都是正整数)
底数可以是一个 也可是一个 或是一个 。数单项式多项式
下列算式是否正确，为什么？
1、(x-y)3· (x-y)5=(x-y)8 ( )
2、(x-y)2·(y-x)2=(x-y)4 ( )√√练一练能力提高： 计算下列各式,结果用幂的形式表示： 本节课你学到了什么？分层作业：必做题：
课本78页 习题11.1 第1题。选做题：
课本78页 习题11.1
第4题（3）（4）
多项式。
谢谢大家！填一填：(1) x4? = x9
(2) (-y)4 ? =(-y)11
(3) a2m ? =a3m
(4) (x-y)2 ? =(x-y)5x5(-y)7am(x-y)3 1、问题 am+n 可以写成哪两个因式的积？
2、如果 xm =3, xn =2, 6能力提升那么 xm+n =____，x2m = ， x2n = 。94 3、如果 8=2x,那么x= ,
如果8×4=2x,那么x= 。 35