湘教版数学七年级下册 4.3平行线的性质 教案
文档属性
| 名称 | 湘教版数学七年级下册 4.3平行线的性质 教案 | 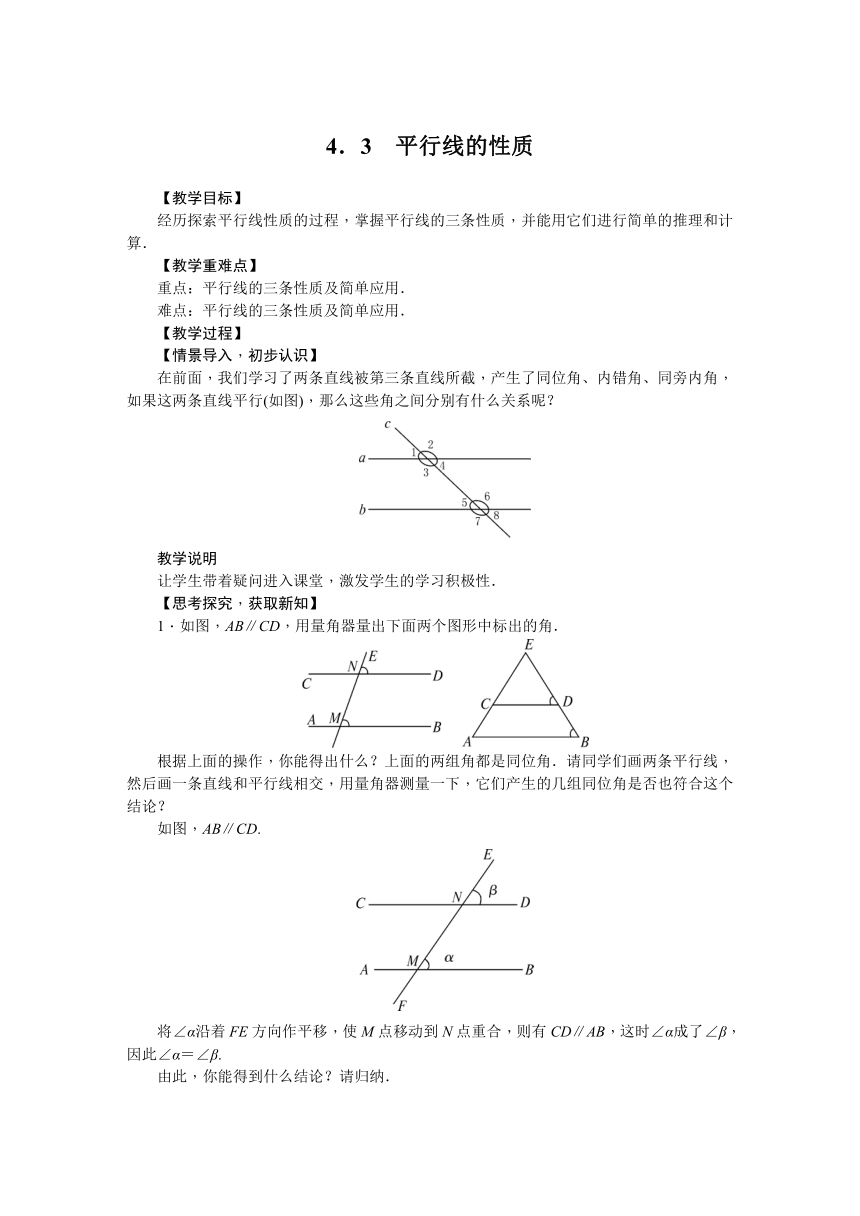 | |
| 格式 | docx | ||
| 文件大小 | 86.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 23:05:22 | ||
图片预览


文档简介
4.3 平行线的性质
【教学目标】
经历探索平行线性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算.
【教学重难点】
重点:平行线的三条性质及简单应用.
难点:平行线的三条性质及简单应用.
【教学过程】
【情景导入,初步认识】
在前面,我们学习了两条直线被第三条直线所截,产生了同位角、内错角、同旁内角,如果这两条直线平行(如图),那么这些角之间分别有什么关系呢?
教学说明
让学生带着疑问进入课堂,激发学生的学习积极性.
【思考探究,获取新知】
1.如图,AB∥CD,用量角器量出下面两个图形中标出的角.
根据上面的操作,你能得出什么?上面的两组角都是同位角.请同学们画两条平行线,然后画一条直线和平行线相交,用量角器测量一下,它们产生的几组同位角是否也符合这个结论?
如图,AB∥CD.
将∠α沿着FE方向作平移,使M点移动到N点重合,则有CD∥AB,这时∠α成了∠β,因此∠α=∠β.
由此,你能得到什么结论?请归纳.
归纳结论
两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.
2.如图,CD∥AB,那么∠1和∠2有什么关系呢?
∵CD∥AB,
∴∠1=∠4(两直线平行,同位角相等).
∵∠2=∠4(对顶角相等),
∴∠1=∠2(等量代换).
由此,你能得到什么结论?请归纳.
归纳结论
两条平行线被第三条直线所截,内错角相等.简单地说成:两直线平行,内错角相等.
3.如图,CD∥AB,那么∠1和∠3有什么关系呢?
∵CD∥AB,
∴∠1=∠2(两直线平行,内错角相等).
∵∠2+∠3=180°,
∴∠1+∠3=180°(等量代换).
由此,你能得到什么结论?请归纳.
归纳结论
两条平行线被第三条直线所截,同旁内角互补.简单地说成:两直线平行,同旁内角互补.
教学说明
通过测量、猜想、验证,让学生在动手探索的过程中感知平行线的性质.
【运用新知,深化理解】
1.见教材P87例1、例2.
2.如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°,则∠DBC的度数为( A )
A.55° B.65° C.75° D.125°
第2题图第3题图
3.如图,直线c与直线a、b相交,且a//b,则下列结论:(1)∠1=∠2;(2)∠1=∠3;(3)∠3=∠2中正确的个数为( D )
A.0 B.1 C.2 D.3
4.如果两条直线被第三条直线所截,那么一组内错角的平分线( D )
A.互相垂直 B.互相平行
C.互相重合 D.以上均不正确
5.如图已知∠1=∠2,∠BAD=∠BCD,则下列结论(1)AB∥CD,(2)AD∥BC,(3)∠B=∠D,(4)∠D=∠ACB,正确的有( C )
A.1个 B.2个 C.3个 D.4个
第5题图第6题图
6.如图,如果∠1=∠2,那么∠2+∠3=180°吗?为什么?
解:∵∠1=∠2,∴l1∥l2.
∴∠2+∠3=180°(两条直线平行,同旁内角互补).
7.如图,AB∥CD,BF∥CE,则∠B与∠C有什么关系?请说明理由.
解:∵AB∥CD,
∴∠B=∠1.
∵BF∥CE,
∴∠C=∠2.
∵∠1+∠2=180°,
∴∠B+∠C=180°.
即∠B与∠C互补.
8.如图,已知:DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.
解:∵CD是∠ACB的平分线,
∴∠ACD=∠BCD.
∵∠ACB=50°,
∴∠BCD=25°.
∵DE∥BC,
∴∠EDC=∠BCD=25°.
∵DE∥BC,∴∠BDE+∠B=180°.
∴∠BDE=180°-∠B=110°.
∴∠BDC=85°.
9.如图,已知AB∥CD,∠1=∠2,试探索∠BEF与∠EFC之间的关系,并说明理由.
解:∠BEF=∠EFC.理由如下:
分别延长BE、DC相交于点G.
∵AB∥CD,
∴∠1=∠G(两直线平行,内错角相等).
∵∠1=∠2,∴∠2=∠G,
∴BE∥FC.
∴∠BEF=∠EFC(两直线平行,内错角相等).
【师生互动,课堂小结】
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
【课后作业】
1.布置作业:教材“习题4.3”中第3、4、6题.
2.完成同步练习册中本课时的练习.
【教学目标】
经历探索平行线性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算.
【教学重难点】
重点:平行线的三条性质及简单应用.
难点:平行线的三条性质及简单应用.
【教学过程】
【情景导入,初步认识】
在前面,我们学习了两条直线被第三条直线所截,产生了同位角、内错角、同旁内角,如果这两条直线平行(如图),那么这些角之间分别有什么关系呢?
教学说明
让学生带着疑问进入课堂,激发学生的学习积极性.
【思考探究,获取新知】
1.如图,AB∥CD,用量角器量出下面两个图形中标出的角.
根据上面的操作,你能得出什么?上面的两组角都是同位角.请同学们画两条平行线,然后画一条直线和平行线相交,用量角器测量一下,它们产生的几组同位角是否也符合这个结论?
如图,AB∥CD.
将∠α沿着FE方向作平移,使M点移动到N点重合,则有CD∥AB,这时∠α成了∠β,因此∠α=∠β.
由此,你能得到什么结论?请归纳.
归纳结论
两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.
2.如图,CD∥AB,那么∠1和∠2有什么关系呢?
∵CD∥AB,
∴∠1=∠4(两直线平行,同位角相等).
∵∠2=∠4(对顶角相等),
∴∠1=∠2(等量代换).
由此,你能得到什么结论?请归纳.
归纳结论
两条平行线被第三条直线所截,内错角相等.简单地说成:两直线平行,内错角相等.
3.如图,CD∥AB,那么∠1和∠3有什么关系呢?
∵CD∥AB,
∴∠1=∠2(两直线平行,内错角相等).
∵∠2+∠3=180°,
∴∠1+∠3=180°(等量代换).
由此,你能得到什么结论?请归纳.
归纳结论
两条平行线被第三条直线所截,同旁内角互补.简单地说成:两直线平行,同旁内角互补.
教学说明
通过测量、猜想、验证,让学生在动手探索的过程中感知平行线的性质.
【运用新知,深化理解】
1.见教材P87例1、例2.
2.如图,一把长方形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°,则∠DBC的度数为( A )
A.55° B.65° C.75° D.125°
第2题图第3题图
3.如图,直线c与直线a、b相交,且a//b,则下列结论:(1)∠1=∠2;(2)∠1=∠3;(3)∠3=∠2中正确的个数为( D )
A.0 B.1 C.2 D.3
4.如果两条直线被第三条直线所截,那么一组内错角的平分线( D )
A.互相垂直 B.互相平行
C.互相重合 D.以上均不正确
5.如图已知∠1=∠2,∠BAD=∠BCD,则下列结论(1)AB∥CD,(2)AD∥BC,(3)∠B=∠D,(4)∠D=∠ACB,正确的有( C )
A.1个 B.2个 C.3个 D.4个
第5题图第6题图
6.如图,如果∠1=∠2,那么∠2+∠3=180°吗?为什么?
解:∵∠1=∠2,∴l1∥l2.
∴∠2+∠3=180°(两条直线平行,同旁内角互补).
7.如图,AB∥CD,BF∥CE,则∠B与∠C有什么关系?请说明理由.
解:∵AB∥CD,
∴∠B=∠1.
∵BF∥CE,
∴∠C=∠2.
∵∠1+∠2=180°,
∴∠B+∠C=180°.
即∠B与∠C互补.
8.如图,已知:DE∥BC,CD是∠ACB的平分线,∠B=70°,∠ACB=50°,求∠EDC和∠BDC的度数.
解:∵CD是∠ACB的平分线,
∴∠ACD=∠BCD.
∵∠ACB=50°,
∴∠BCD=25°.
∵DE∥BC,
∴∠EDC=∠BCD=25°.
∵DE∥BC,∴∠BDE+∠B=180°.
∴∠BDE=180°-∠B=110°.
∴∠BDC=85°.
9.如图,已知AB∥CD,∠1=∠2,试探索∠BEF与∠EFC之间的关系,并说明理由.
解:∠BEF=∠EFC.理由如下:
分别延长BE、DC相交于点G.
∵AB∥CD,
∴∠1=∠G(两直线平行,内错角相等).
∵∠1=∠2,∴∠2=∠G,
∴BE∥FC.
∴∠BEF=∠EFC(两直线平行,内错角相等).
【师生互动,课堂小结】
先小组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
【课后作业】
1.布置作业:教材“习题4.3”中第3、4、6题.
2.完成同步练习册中本课时的练习.
