8.2.1两角和与差的余弦 学案(Word版无答案)
文档属性
| 名称 | 8.2.1两角和与差的余弦 学案(Word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 164.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 16:02:07 | ||
图片预览


文档简介
两角和与差的余弦
【学习目标】
1.探索、猜想、发现并推导公式;熟悉公式的结构、加深公式的理解。
2.能用余弦的和差角公式进行简单的三角函数式的化简、求值及恒等式证明
【学习重难点】
两角和与差的余弦公式的理解与灵活运用。
【学习过程】
一、预习内容
(1)向量的数量积
则
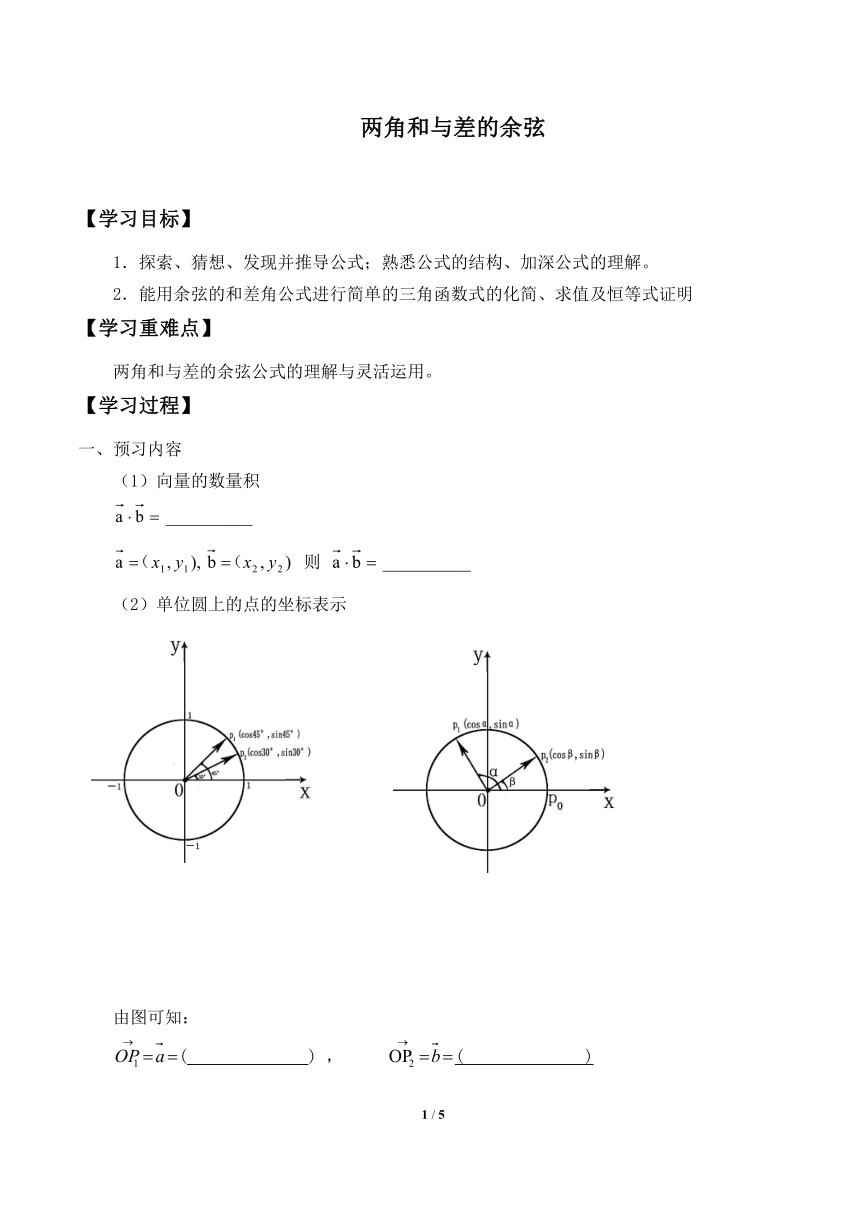
(2)单位圆上的点的坐标表示
由图可知:
( ) , ( )
则
二、新知学习
(小组交流)
问题1:
问题2 :由出发,你能推广到对任意的两个角都成立吗?
问题3: 两角和的余弦公式:
两角差的余弦公式:
三、新知深化
1.公式中两边的符号正好相反(一正一负);
2.式子右边同名三角函数相乘再加减,且余弦在前正弦在后;
3.式子中α、β是任意的。
4.式子的逆用,变形用
四、互相交流 小组活动 公式应用闯关
1.请用特殊角分别代替公式中α、β,你能求哪些非特殊角的余弦值呢?(选择的特殊角可以是30°60°45°等)
(1)
(2)
(3)
……
2.若β固定,分别用 代替α,你将会发现什么结论呢?[
3.倘若让你对C(α±β)公式中的α、β自由赋值,你又将发现什么结论呢?
(1)
(2)
(3)
(4)
五、新知应用
例1:求下列各式的值。
(1)
(2)
(3)
例2:已知,求的值。
变题:
六、新知回顾
1.牢记公式的结构特点,学会逆用公式。不符合公式结构特点的,常通过诱导公式变形使之符合。
2.强调公式中α、β的任意性,是本节内容的主线,它赋予了公式的强大生命力。
注:逆用公式是学生认识和掌握公式的重要标志。通过步步加深的练习,加强学生对公式的理解和应用,引导学生积极参与思维,培养学生观察,比较等思维能力,同时渗透了一种化归思想。
【达标检测】
1.利用两角和与差的余弦公式证明:
(1); (2)
2.利用两角和与差的余弦公式化简与求值
(1)
(2)=
(3)
3.已知,,求的值
4.(1)cos130°cos5°-sin130°sin5°=
(2)设,若,则
5. (1)已知,求的值。
(2)已知且它们都是第二象限角,求的值。
6. 已知的值
PAGE
1 / 5
【学习目标】
1.探索、猜想、发现并推导公式;熟悉公式的结构、加深公式的理解。
2.能用余弦的和差角公式进行简单的三角函数式的化简、求值及恒等式证明
【学习重难点】
两角和与差的余弦公式的理解与灵活运用。
【学习过程】
一、预习内容
(1)向量的数量积
则
(2)单位圆上的点的坐标表示
由图可知:
( ) , ( )
则
二、新知学习
(小组交流)
问题1:
问题2 :由出发,你能推广到对任意的两个角都成立吗?
问题3: 两角和的余弦公式:
两角差的余弦公式:
三、新知深化
1.公式中两边的符号正好相反(一正一负);
2.式子右边同名三角函数相乘再加减,且余弦在前正弦在后;
3.式子中α、β是任意的。
4.式子的逆用,变形用
四、互相交流 小组活动 公式应用闯关
1.请用特殊角分别代替公式中α、β,你能求哪些非特殊角的余弦值呢?(选择的特殊角可以是30°60°45°等)
(1)
(2)
(3)
……
2.若β固定,分别用 代替α,你将会发现什么结论呢?[
3.倘若让你对C(α±β)公式中的α、β自由赋值,你又将发现什么结论呢?
(1)
(2)
(3)
(4)
五、新知应用
例1:求下列各式的值。
(1)
(2)
(3)
例2:已知,求的值。
变题:
六、新知回顾
1.牢记公式的结构特点,学会逆用公式。不符合公式结构特点的,常通过诱导公式变形使之符合。
2.强调公式中α、β的任意性,是本节内容的主线,它赋予了公式的强大生命力。
注:逆用公式是学生认识和掌握公式的重要标志。通过步步加深的练习,加强学生对公式的理解和应用,引导学生积极参与思维,培养学生观察,比较等思维能力,同时渗透了一种化归思想。
【达标检测】
1.利用两角和与差的余弦公式证明:
(1); (2)
2.利用两角和与差的余弦公式化简与求值
(1)
(2)=
(3)
3.已知,,求的值
4.(1)cos130°cos5°-sin130°sin5°=
(2)设,若,则
5. (1)已知,求的值。
(2)已知且它们都是第二象限角,求的值。
6. 已知的值
PAGE
1 / 5
