人教版六年级下学期数学3.1.2圆柱的表面积课件(共20张PPT)
文档属性
| 名称 | 人教版六年级下学期数学3.1.2圆柱的表面积课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
圆柱的表面积
根据具体情境,灵活运用圆柱表面积的计算方法解决生活中一些简单的问题,使学生感受到数学与生活的密切联系
通过想象、操作等活动,知道圆柱侧面展开后可以是一个长方形,加深对圆柱特征的认识,发展空间观念。
3. 结合具体情境和动手操作,探索圆柱侧面积的计算方法,掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
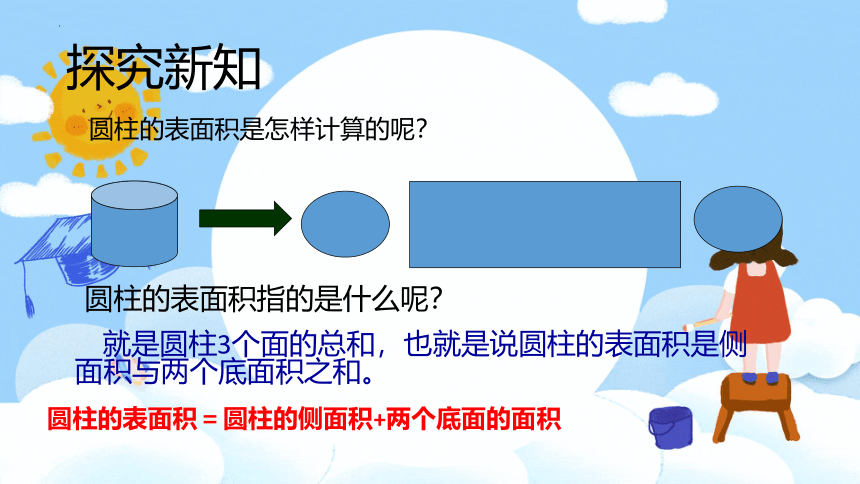
探究新知
圆柱的表面积是怎样计算的呢?
圆柱的表面积指的是什么呢?
就是圆柱3个面的总和,也就是说圆柱的表面积是侧面积与两个底面积之和。
圆柱的表面积=圆柱的侧面积+两个底面的面积
提出问题
一顶圆柱形的厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
30cm
20cm
课程引入
同学们去商场是否看到很多广告柱子?这些柱子=就是一个圆柱。生活中有很多物体都是圆柱状态,同学们可以举例子吗?
这节课将要用圆柱表面积知识解决实际问题。
这些物体的形状有什么共同特点?
随堂演练
1.下面图形哪些是圆柱?请对应在( )里画“√”
√
√
√
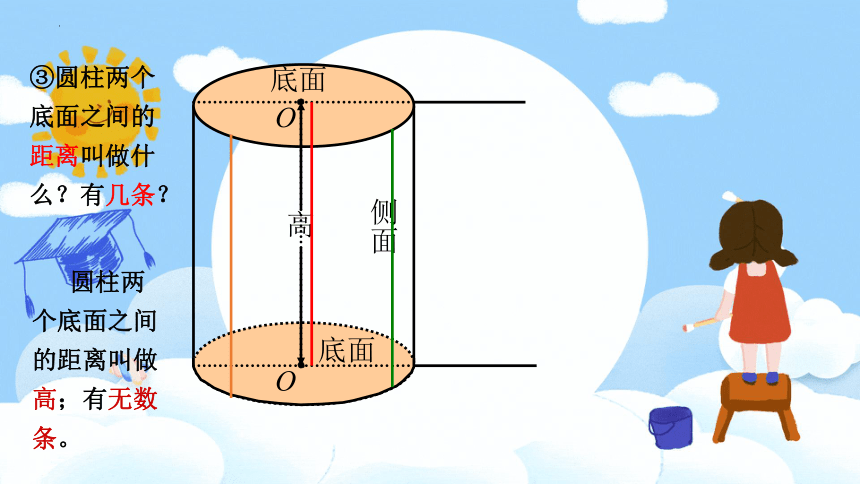
底面
底面
侧面
高
O
O
③圆柱两个底面之间的距离叫做什么?有几条?
圆柱两个底面之间的距离叫做高;有无数条。
S= d+2 r2
=2 r+2 r2
探究新知
圆柱的表面积
=侧面积 + 2 ×底面积
=底面周长×高 + 2 ×3.14 ×(底面半径)
=底面直径×3.14 ×高 + 2 ×3.14 × (底面半径)
=底面半径×2 ×3.14 ×高+ 2 ×3.14 × (底面半径)
2
2
2
易错举例
圆柱的侧面展开图不可能是一个( )。
A.长方形 B.正方形
C.梯形 D.平行四边形
我选D
×
C
正确答案应该选D。
(1).如果圆柱的底面周长与高相等,把圆柱的侧面展开:①沿高线剪开:圆柱的侧面展开图是一个正方形;②不沿高线剪:斜着剪开将会得到一个平行四边形。
(2).如果圆柱的底面周长与高不相等,把圆柱的侧面展开:①沿高线剪开:圆柱的侧面展开图是一个长方形;②不沿高线剪:斜着剪开将会得到一个平行四边形或菱形。
综上:圆柱的侧面展开图不能是梯形。
(1)为生日蛋糕选择一个合适的蛋糕盒。
(2)做这个生日蛋糕需要多少硬纸板?
例1:小李家里有一个无盖圆柱形铁水桶,高是45厘米,底面直径是40厘米。这个水桶需要多少铁皮?
(1)水桶的侧面积:
S侧=πdh= 40×3.14×45=5652(平方厘米)
(2)水桶的底面积:
S底=πr2=3.14×(40÷2)2=1256(平方厘米)
(3)至少需要多少铁皮:
5652+1256=6908(平方厘米)
答:至少需要6908平方厘米的铁皮。
一个圆柱形水池,水池内壁和底部都镶上磁砖,
水池内部底面周长25.12m,池深1.2m,镶磁砖的
面积是多少平方米?
求圆柱侧面积和一个底面积
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
侧面积:25.12×1.2=30.144(m2)
表面积:30.144+50.24=80.384(m2)
课堂练习
计算下面圆柱的表面积(图中单位:cm)
(1)圆柱的侧面积:
3.14×5×20=314(cm2)
(2)圆柱的底面积:
3.14×(5÷2)2×2=39.25(cm2) (3)圆柱的表面积:
314+39.25=353.25(cm2)
20
5
下一张
上一张
首页
底面
底面
侧面展开后的长方形的长和宽与圆柱的什么有关。
课堂小结
实际使用的面料要比计算的结果多一些,因此这类题不能用四舍五入法取整,只能使用“进一法”。这样得到的近似值为过剩近似值。
用进一法凑整时,凑整到哪一位,只要后面的数字不全是0,都向这一位进一,然后再把这一位后面的数都改写成0。
课后作业
完成课后对应内容。
谢谢大家!!
圆柱的表面积
根据具体情境,灵活运用圆柱表面积的计算方法解决生活中一些简单的问题,使学生感受到数学与生活的密切联系
通过想象、操作等活动,知道圆柱侧面展开后可以是一个长方形,加深对圆柱特征的认识,发展空间观念。
3. 结合具体情境和动手操作,探索圆柱侧面积的计算方法,掌握圆柱侧面积和表面积的计算方法,能正确计算圆柱的侧面积和表面积。
探究新知
圆柱的表面积是怎样计算的呢?
圆柱的表面积指的是什么呢?
就是圆柱3个面的总和,也就是说圆柱的表面积是侧面积与两个底面积之和。
圆柱的表面积=圆柱的侧面积+两个底面的面积
提出问题
一顶圆柱形的厨师帽,高30cm,帽顶直径20cm。做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数)
30cm
20cm
课程引入
同学们去商场是否看到很多广告柱子?这些柱子=就是一个圆柱。生活中有很多物体都是圆柱状态,同学们可以举例子吗?
这节课将要用圆柱表面积知识解决实际问题。
这些物体的形状有什么共同特点?
随堂演练
1.下面图形哪些是圆柱?请对应在( )里画“√”
√
√
√
底面
底面
侧面
高
O
O
③圆柱两个底面之间的距离叫做什么?有几条?
圆柱两个底面之间的距离叫做高;有无数条。
S= d+2 r2
=2 r+2 r2
探究新知
圆柱的表面积
=侧面积 + 2 ×底面积
=底面周长×高 + 2 ×3.14 ×(底面半径)
=底面直径×3.14 ×高 + 2 ×3.14 × (底面半径)
=底面半径×2 ×3.14 ×高+ 2 ×3.14 × (底面半径)
2
2
2
易错举例
圆柱的侧面展开图不可能是一个( )。
A.长方形 B.正方形
C.梯形 D.平行四边形
我选D
×
C
正确答案应该选D。
(1).如果圆柱的底面周长与高相等,把圆柱的侧面展开:①沿高线剪开:圆柱的侧面展开图是一个正方形;②不沿高线剪:斜着剪开将会得到一个平行四边形。
(2).如果圆柱的底面周长与高不相等,把圆柱的侧面展开:①沿高线剪开:圆柱的侧面展开图是一个长方形;②不沿高线剪:斜着剪开将会得到一个平行四边形或菱形。
综上:圆柱的侧面展开图不能是梯形。
(1)为生日蛋糕选择一个合适的蛋糕盒。
(2)做这个生日蛋糕需要多少硬纸板?
例1:小李家里有一个无盖圆柱形铁水桶,高是45厘米,底面直径是40厘米。这个水桶需要多少铁皮?
(1)水桶的侧面积:
S侧=πdh= 40×3.14×45=5652(平方厘米)
(2)水桶的底面积:
S底=πr2=3.14×(40÷2)2=1256(平方厘米)
(3)至少需要多少铁皮:
5652+1256=6908(平方厘米)
答:至少需要6908平方厘米的铁皮。
一个圆柱形水池,水池内壁和底部都镶上磁砖,
水池内部底面周长25.12m,池深1.2m,镶磁砖的
面积是多少平方米?
求圆柱侧面积和一个底面积
底面积:3.14×(25.12÷3.14÷2)2=50.24(m2)
侧面积:25.12×1.2=30.144(m2)
表面积:30.144+50.24=80.384(m2)
课堂练习
计算下面圆柱的表面积(图中单位:cm)
(1)圆柱的侧面积:
3.14×5×20=314(cm2)
(2)圆柱的底面积:
3.14×(5÷2)2×2=39.25(cm2) (3)圆柱的表面积:
314+39.25=353.25(cm2)
20
5
下一张
上一张
首页
底面
底面
侧面展开后的长方形的长和宽与圆柱的什么有关。
课堂小结
实际使用的面料要比计算的结果多一些,因此这类题不能用四舍五入法取整,只能使用“进一法”。这样得到的近似值为过剩近似值。
用进一法凑整时,凑整到哪一位,只要后面的数字不全是0,都向这一位进一,然后再把这一位后面的数都改写成0。
课后作业
完成课后对应内容。
谢谢大家!!
