人教版 六年级下学期数学6.4数学思考(课件)(共21张PPT)
文档属性
| 名称 | 人教版 六年级下学期数学6.4数学思考(课件)(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
数学思考
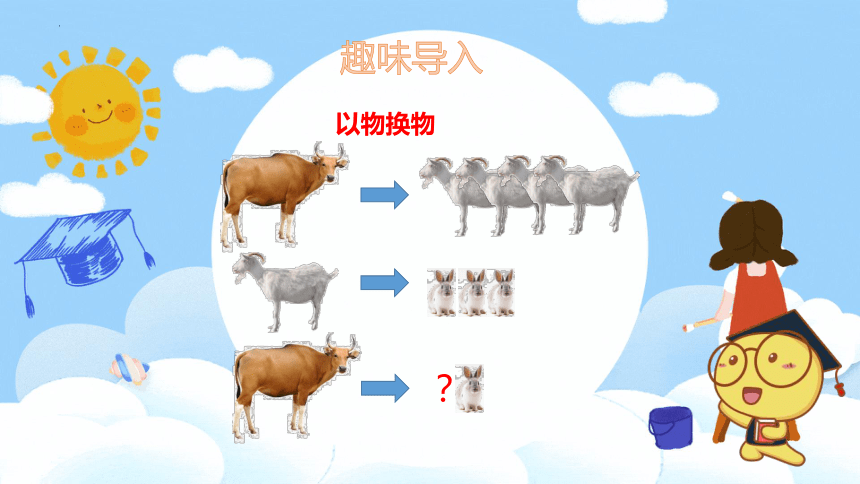
趣味导入
以物换物
?
复习导入
教材第100页
你能举例说一说你知道哪些数学思想和方法吗?
数形结合思想
转化思想
假设法
符号化思想
方程思想
分类思想
类比思想
对应思想
……
数学思想和方法可以帮助我们有条理地思考,简捷地解决问题。
5
1
6
3
10
从第一次到会的情况可以看出,A只可能和D、E、F同班;
A B C D E F
第一次
第二次
第三次
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
从第二次到会的情况可以判断,A只可能和D、E同班;
从第三次到会的情况可以确定,A只可能和D同班。
归纳整理
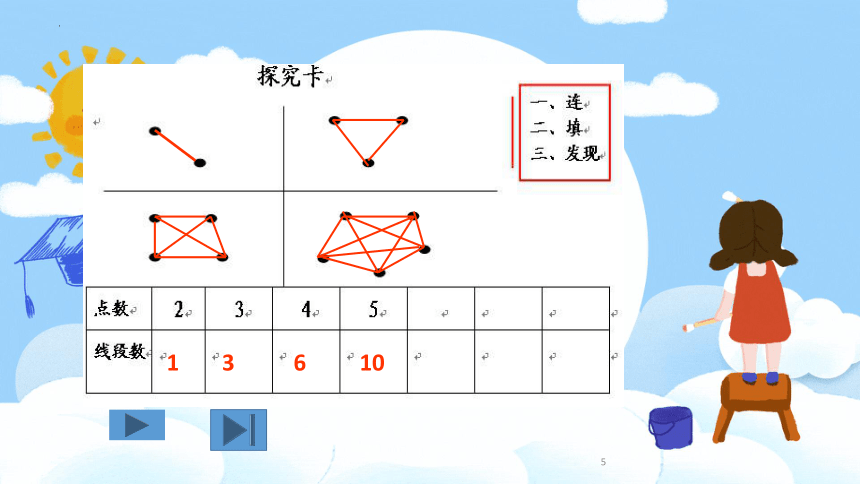
n个点:1+2+3+…+(n-1)
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和。
n个点可以连多少条线段呢?
=n(n-1)÷2(条)(n≥2)
等差数列的和=(首项+尾项)×项数÷2
=[1+(n-1)]×(n-1)÷2
……
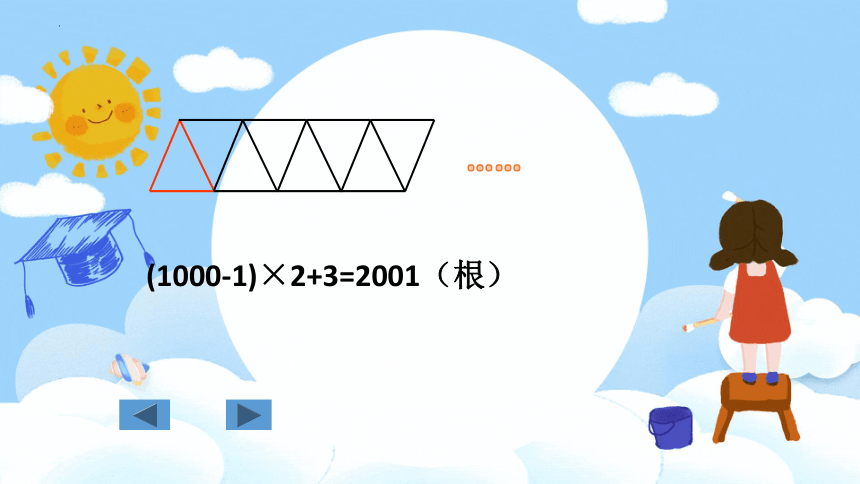
(1000-1)×2+3=2001(根)
新知讲解
小王、小张和小李三人中,一位是工人,一位是农民,一位是军人。已知小李比军人年龄大,小王和农民不同岁,农民比小张年龄小。那么他们中( )是工人,( )是农民,( )是军人。
小王 小张 小李
工人
农民
军人
×
√
√
×
√
列表,是就打“√”,不是打“×”。
小李
×
农民比小张年龄小
小李比小张年龄小
小李比军人年龄大
×
小张
小王
总条数
增加条数
点数
2
3
4
5
6
1
2
3
3
6
10
4
5
15
思考:每次增加的条数和点数间有什么规律?
每次增加的条数比点数少1。
数学思考数学思考
A
B
总条数
增加条数
点数
2
1
3
4
5
6
按规律填数。
(1)8、11、14、17、( )、23、……
+3
+3
+3
+3
20
+3
(2)一列数1、2、2、3、3、3、4、4、4、4、……中的第35个数是( )
1个1
2个2
3个3
4个4
+ + + + 5 + 6 + 7 + 8 =36
8
第36个数是第8个8,第35个数是第7个8。
新知讲解
将两种图形转化成一种图形
将▲换成█
明明、强强和亮亮三个男生各有一个妹妹,六个人在一起举行羽毛球混合双打比赛,赛前规定兄妹二人不可以搭档。第一轮,明明和小花对阵亮亮和小红;第二轮,亮亮和小林对阵明明和强强的妹妹。请判断小花、小红和小林分别是谁的妹妹?
明明 强强 亮亮
小花
小红
小林
×
√
√
×
√
×
×
“兄妹二人不可以搭档”则搭档的两人一定不是兄妹。
…
(2)第( )个图形中,白三角形比黄三角形多2021个。
2020
第1个
第2个
第3个
多2个
多3个
多4个
2021-1=2020(个)
如图所示的三个图形都是用同样大小的三角形按一定规律拼成的一组图形。
新知讲解
想一想
(2)○+☆=160,◎+☆=160。
○是否等于◎?
请你用自己喜欢的方法解决问题。
13个城市,每两个城市之间交流一次,共交流多少次?
新知讲解
因为○+☆=160,◎+☆=160
所以○=160-☆,◎=160-☆
因为160-☆=160-☆
所以○=◎
一个加数=和-另一个加数
新知讲解
应用等式性质将题目中☆抵消
21
谢谢大家!!
数学思考
趣味导入
以物换物
?
复习导入
教材第100页
你能举例说一说你知道哪些数学思想和方法吗?
数形结合思想
转化思想
假设法
符号化思想
方程思想
分类思想
类比思想
对应思想
……
数学思想和方法可以帮助我们有条理地思考,简捷地解决问题。
5
1
6
3
10
从第一次到会的情况可以看出,A只可能和D、E、F同班;
A B C D E F
第一次
第二次
第三次
1
1
1
0
0
0
0
1
0
1
1
0
1
0
0
0
1
1
从第二次到会的情况可以判断,A只可能和D、E同班;
从第三次到会的情况可以确定,A只可能和D同班。
归纳整理
n个点:1+2+3+…+(n-1)
计算有几条线段,就是从1+2+3+…一直加到比点数少1的数再求和。
n个点可以连多少条线段呢?
=n(n-1)÷2(条)(n≥2)
等差数列的和=(首项+尾项)×项数÷2
=[1+(n-1)]×(n-1)÷2
……
(1000-1)×2+3=2001(根)
新知讲解
小王、小张和小李三人中,一位是工人,一位是农民,一位是军人。已知小李比军人年龄大,小王和农民不同岁,农民比小张年龄小。那么他们中( )是工人,( )是农民,( )是军人。
小王 小张 小李
工人
农民
军人
×
√
√
×
√
列表,是就打“√”,不是打“×”。
小李
×
农民比小张年龄小
小李比小张年龄小
小李比军人年龄大
×
小张
小王
总条数
增加条数
点数
2
3
4
5
6
1
2
3
3
6
10
4
5
15
思考:每次增加的条数和点数间有什么规律?
每次增加的条数比点数少1。
数学思考数学思考
A
B
总条数
增加条数
点数
2
1
3
4
5
6
按规律填数。
(1)8、11、14、17、( )、23、……
+3
+3
+3
+3
20
+3
(2)一列数1、2、2、3、3、3、4、4、4、4、……中的第35个数是( )
1个1
2个2
3个3
4个4
+ + + + 5 + 6 + 7 + 8 =36
8
第36个数是第8个8,第35个数是第7个8。
新知讲解
将两种图形转化成一种图形
将▲换成█
明明、强强和亮亮三个男生各有一个妹妹,六个人在一起举行羽毛球混合双打比赛,赛前规定兄妹二人不可以搭档。第一轮,明明和小花对阵亮亮和小红;第二轮,亮亮和小林对阵明明和强强的妹妹。请判断小花、小红和小林分别是谁的妹妹?
明明 强强 亮亮
小花
小红
小林
×
√
√
×
√
×
×
“兄妹二人不可以搭档”则搭档的两人一定不是兄妹。
…
(2)第( )个图形中,白三角形比黄三角形多2021个。
2020
第1个
第2个
第3个
多2个
多3个
多4个
2021-1=2020(个)
如图所示的三个图形都是用同样大小的三角形按一定规律拼成的一组图形。
新知讲解
想一想
(2)○+☆=160,◎+☆=160。
○是否等于◎?
请你用自己喜欢的方法解决问题。
13个城市,每两个城市之间交流一次,共交流多少次?
新知讲解
因为○+☆=160,◎+☆=160
所以○=160-☆,◎=160-☆
因为160-☆=160-☆
所以○=◎
一个加数=和-另一个加数
新知讲解
应用等式性质将题目中☆抵消
21
谢谢大家!!
