四年级下学期数学第九单元9数学广角-鸡兔同笼课件(共18张PPT)
文档属性
| 名称 | 四年级下学期数学第九单元9数学广角-鸡兔同笼课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 32.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 14:57:17 | ||
图片预览






文档简介
(共18张PPT)
数学广角-鸡兔同笼
上卷叙述算筹计数的制度和乘除法则
中卷举例说明筹算分数法和开平方法
下卷收集了一些算术趣题
你有方法吗?
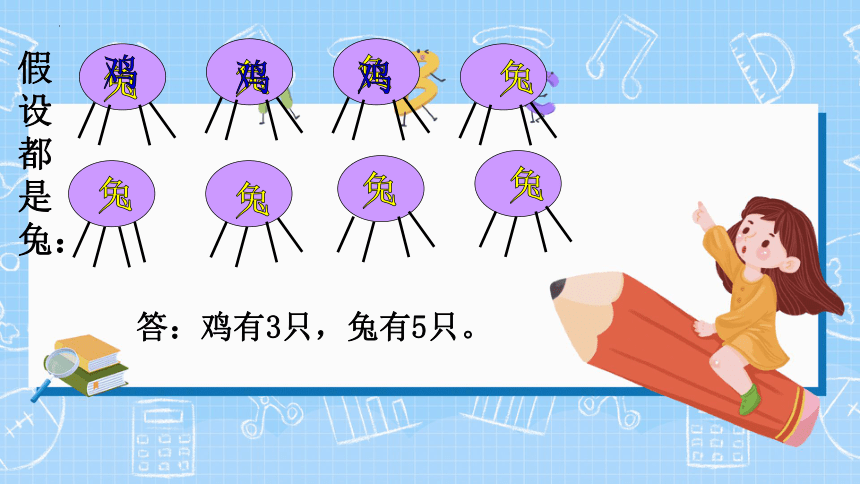
兔
兔
兔
兔
兔
兔
兔
鸡
鸡
鸡
兔
答:鸡有3只,兔有5只。
假设都是兔:
假设法(三):都是兔子
如果设想88只都是兔子,那么就有4×88只脚,比244只脚多了:
88×4-244=108(只)。
每只鸡比兔子少(4-2)只脚,所以共有鸡
(88×4-244)÷(4-2)= 54(只)。
说明我们设想的88只“兔子”中,有54只不是兔子。而是鸡。因此可以列出公式:
鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)
经典例题1
26÷2=13(条)
13-8 = 5(只)
8-5=3(只)
兔子
鸡
有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?
日本的“龟鹤算”
问题就是从我国的
“鸡兔同笼”问题
演变来的。
40×2=80 (条)
112-80=32 (条)
32÷2=16 (只)--- (龟)
40-16=24 (只)--- (鹤)
答:龟有16只,鹤有24只
专题总结
1、灵活运用假设法和“抬脚法”解决鸡兔同笼问题。
分组法
例:100个和尚吃100个馒头,1个大和尚吃3个馒头,3个小和尚吃1个馒头,几个大和尚几个小和尚?
作业:
第105页做一做第2题.
第106页练习二十四第2、3题。
同学们再见
数学广角-鸡兔同笼
上卷叙述算筹计数的制度和乘除法则
中卷举例说明筹算分数法和开平方法
下卷收集了一些算术趣题
你有方法吗?
兔
兔
兔
兔
兔
兔
兔
鸡
鸡
鸡
兔
答:鸡有3只,兔有5只。
假设都是兔:
假设法(三):都是兔子
如果设想88只都是兔子,那么就有4×88只脚,比244只脚多了:
88×4-244=108(只)。
每只鸡比兔子少(4-2)只脚,所以共有鸡
(88×4-244)÷(4-2)= 54(只)。
说明我们设想的88只“兔子”中,有54只不是兔子。而是鸡。因此可以列出公式:
鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)
经典例题1
26÷2=13(条)
13-8 = 5(只)
8-5=3(只)
兔子
鸡
有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?
日本的“龟鹤算”
问题就是从我国的
“鸡兔同笼”问题
演变来的。
40×2=80 (条)
112-80=32 (条)
32÷2=16 (只)--- (龟)
40-16=24 (只)--- (鹤)
答:龟有16只,鹤有24只
专题总结
1、灵活运用假设法和“抬脚法”解决鸡兔同笼问题。
分组法
例:100个和尚吃100个馒头,1个大和尚吃3个馒头,3个小和尚吃1个馒头,几个大和尚几个小和尚?
作业:
第105页做一做第2题.
第106页练习二十四第2、3题。
同学们再见
