24.2.2 圆的切线教学 课件(共21张PPT)
文档属性
| 名称 | 24.2.2 圆的切线教学 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 942.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-19 19:42:47 | ||
图片预览







文档简介
(共21张PPT)
圆的切线
人教版九年级上册
教学目标
(1)知识与技能:1.能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.
2.理解圆的切线的性质,并能解决简单的实际问题.
(2)过程与方法:1.通过观察得出“圆心到直线的距离d和半径r的数量关系”与“直线和圆的位置关系”的对应
与等价,从而实现位置关系与数量关系的相互转化.
2.通过对圆的切线的判定定理的逆向思想,经历探究圆的切线的性质的过程,体会几何学习的
一种方法与途径.
3.经历圆的切线的判定、性质的探索过程,培养学生的探索能力.
(3)情感态度价值观:通过经历圆的切线的判定、性质的探索过程,体验数学活动充满着探索与创造,
感受数学的严谨性以及数学结论的确定性.
新知导入
问题1:
什么叫做点到直线的距离?如图,请作出点A到直l线的距离.
问题2:直线与圆与几种位置关系?怎样去判断?
今天我们重点研究直线和圆相切的情况.
一、导(忆一忆)
新知讲解
二、学(阅读教材)
问题:阅读教材97-98页.
然后完成下列活动
新知讲解
三、探(自主探究)
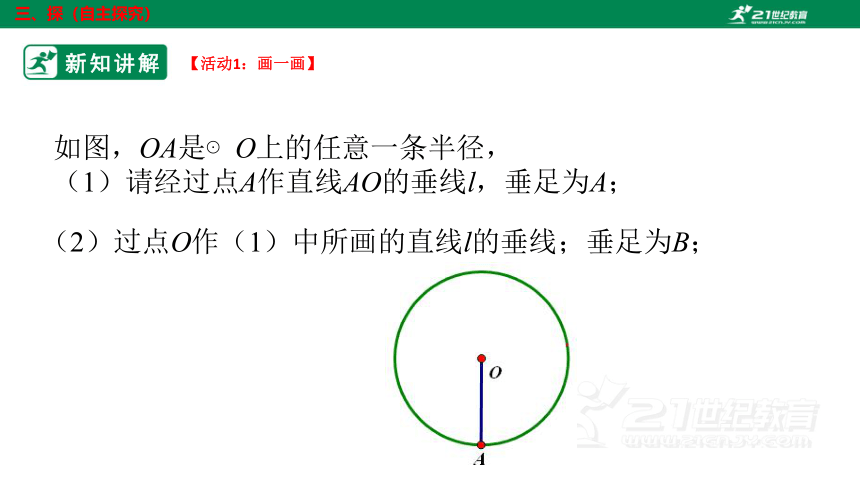
【活动1:画一画】
如图,OA是⊙O上的任意一条半径,
(1)请经过点A作直线AO的垂线l,垂足为A;
(2)过点O作(1)中所画的直线l的垂线;垂足为B;
新知讲解
三、探(自主探究)
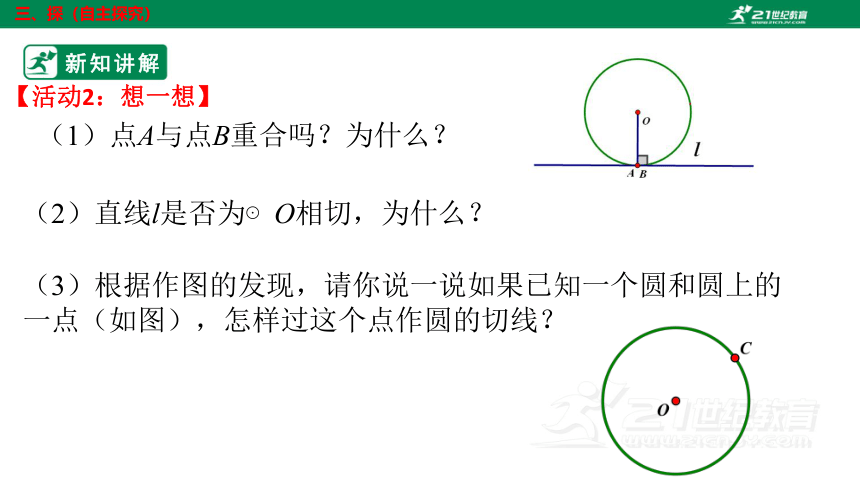
【活动2:想一想】
(1)点A与点B重合吗?为什么?
(2)直线l是否为⊙O相切,为什么?
(3)根据作图的发现,请你说一说如果已知一个圆和圆上的一点(如图),怎样过这个点作圆的切线?
新知讲解
三、探(合作探究)
请同学说说一说这个命题的条件、结论;
【活动3:理一理】
猜想:如果一条直线经过半径的外端点,并且垂直于这条半径,那么这条直线就是圆的切线。
新知讲解
三、探(自主探究)
【活动3:理一理】
切线的判定定理:如果一条直线经过半径的外端点,并且垂直于这条半径,那么这条直线就是圆的切线。
简称:经过半径的外端并且垂直于这条半径的
直线是圆的切线。
新知讲解
三、探(自主探究)
由此,我们发现: 切线的判定定理成立有两个前提条件:
①: ;②: ;
【活动4:判一判】
(1)经过一条半径外端的直线是圆的切线;( )
(2)垂直与一条半径的直线是圆的切线;( )
(3)经过一条半径的端点并且垂直于这条半径
的直线是圆的切线;( )
切线的判定定理的作用是: ;
新知讲解
三、探(自主探究)
这个命题是否正确?请说出你的理由。
交换切线的判定定理的题设和结论,得到命题:
【活动5:换一换】
如果一条直线是圆的切线,那么这条直线
垂直于过切点的半径;
新知讲解
三、探(自主探究)
【活动6:连一连】
如图,直线l是⊙O的切线,切点是A,
(1)请完成作图:连接OA;
(2)请根据你的作图,判断半径OA与切线l是否垂直?
新知讲解
三、探(合作探究)
【活动7:证一证】
切线l与半径OA垂直,你能证明吗?
圆的切线性质:
如果一条直线是圆的切线,那么这条直线垂直于过切点的半径;
简单说成:圆的切线垂直于过切点的半径
新知讲解
三、探(自主探究)
【活动8:判一判】
(1)圆的切线垂直于圆的半径;( );
(2)任意一条直线垂直于过切点的半径( )(3)圆的割线垂直于过切点的半径( );
(4)圆的切线垂直于过过切点的半径( )
由此,我们发现:
切线的性质定理的前提条件: ;
得出的结论: ;
切线的性质定理的作用是: ;
新知讲解
三、探(自主探究)
【例1】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
新知讲解
三、探(自主探究)
【例2】如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为8cm,
AB=10cm,求OA的长;
课堂练习
四、测
1、[2018·湘潭]如图,AB是⊙O的切线,点B为切点,若∠A=30°,则∠AOB= ;
2、[2018·长沙]如图,点A,B,D在⊙O上,∠A=20°,BC是圆的切线,B为切点,OD的延长线交BC于点C,则∠OCB= 度.
课堂总结
本课时重点:
切线的性质定理:圆的切线垂直于过切点的半径
切线的判定定理:经过半径的外端并且垂直于
这条半径的直线是圆的切线;
板书设计
作业布置
必做题:教材P98页练习1,2
选做题:教材P101 第4题
教材P102 第12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
圆的切线
人教版九年级上册
教学目标
(1)知识与技能:1.能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.
2.理解圆的切线的性质,并能解决简单的实际问题.
(2)过程与方法:1.通过观察得出“圆心到直线的距离d和半径r的数量关系”与“直线和圆的位置关系”的对应
与等价,从而实现位置关系与数量关系的相互转化.
2.通过对圆的切线的判定定理的逆向思想,经历探究圆的切线的性质的过程,体会几何学习的
一种方法与途径.
3.经历圆的切线的判定、性质的探索过程,培养学生的探索能力.
(3)情感态度价值观:通过经历圆的切线的判定、性质的探索过程,体验数学活动充满着探索与创造,
感受数学的严谨性以及数学结论的确定性.
新知导入
问题1:
什么叫做点到直线的距离?如图,请作出点A到直l线的距离.
问题2:直线与圆与几种位置关系?怎样去判断?
今天我们重点研究直线和圆相切的情况.
一、导(忆一忆)
新知讲解
二、学(阅读教材)
问题:阅读教材97-98页.
然后完成下列活动
新知讲解
三、探(自主探究)
【活动1:画一画】
如图,OA是⊙O上的任意一条半径,
(1)请经过点A作直线AO的垂线l,垂足为A;
(2)过点O作(1)中所画的直线l的垂线;垂足为B;
新知讲解
三、探(自主探究)
【活动2:想一想】
(1)点A与点B重合吗?为什么?
(2)直线l是否为⊙O相切,为什么?
(3)根据作图的发现,请你说一说如果已知一个圆和圆上的一点(如图),怎样过这个点作圆的切线?
新知讲解
三、探(合作探究)
请同学说说一说这个命题的条件、结论;
【活动3:理一理】
猜想:如果一条直线经过半径的外端点,并且垂直于这条半径,那么这条直线就是圆的切线。
新知讲解
三、探(自主探究)
【活动3:理一理】
切线的判定定理:如果一条直线经过半径的外端点,并且垂直于这条半径,那么这条直线就是圆的切线。
简称:经过半径的外端并且垂直于这条半径的
直线是圆的切线。
新知讲解
三、探(自主探究)
由此,我们发现: 切线的判定定理成立有两个前提条件:
①: ;②: ;
【活动4:判一判】
(1)经过一条半径外端的直线是圆的切线;( )
(2)垂直与一条半径的直线是圆的切线;( )
(3)经过一条半径的端点并且垂直于这条半径
的直线是圆的切线;( )
切线的判定定理的作用是: ;
新知讲解
三、探(自主探究)
这个命题是否正确?请说出你的理由。
交换切线的判定定理的题设和结论,得到命题:
【活动5:换一换】
如果一条直线是圆的切线,那么这条直线
垂直于过切点的半径;
新知讲解
三、探(自主探究)
【活动6:连一连】
如图,直线l是⊙O的切线,切点是A,
(1)请完成作图:连接OA;
(2)请根据你的作图,判断半径OA与切线l是否垂直?
新知讲解
三、探(合作探究)
【活动7:证一证】
切线l与半径OA垂直,你能证明吗?
圆的切线性质:
如果一条直线是圆的切线,那么这条直线垂直于过切点的半径;
简单说成:圆的切线垂直于过切点的半径
新知讲解
三、探(自主探究)
【活动8:判一判】
(1)圆的切线垂直于圆的半径;( );
(2)任意一条直线垂直于过切点的半径( )(3)圆的割线垂直于过切点的半径( );
(4)圆的切线垂直于过过切点的半径( )
由此,我们发现:
切线的性质定理的前提条件: ;
得出的结论: ;
切线的性质定理的作用是: ;
新知讲解
三、探(自主探究)
【例1】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
新知讲解
三、探(自主探究)
【例2】如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为8cm,
AB=10cm,求OA的长;
课堂练习
四、测
1、[2018·湘潭]如图,AB是⊙O的切线,点B为切点,若∠A=30°,则∠AOB= ;
2、[2018·长沙]如图,点A,B,D在⊙O上,∠A=20°,BC是圆的切线,B为切点,OD的延长线交BC于点C,则∠OCB= 度.
课堂总结
本课时重点:
切线的性质定理:圆的切线垂直于过切点的半径
切线的判定定理:经过半径的外端并且垂直于
这条半径的直线是圆的切线;
板书设计
作业布置
必做题:教材P98页练习1,2
选做题:教材P101 第4题
教材P102 第12题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
