【中考专题复习-几何图形与函数专题】第1课时 圆与等积(比例)线段(含答案)
文档属性
| 名称 | 【中考专题复习-几何图形与函数专题】第1课时 圆与等积(比例)线段(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 260.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第2章 几何图形与函数专题
第 1课时 等腰三角形存在性模型
【一、模型构建】
请在直线l上找一点P,使△PAB为等腰三角形:
【二、典型例题】
【例1】如图,抛物线与轴交于A、B两点,与轴交于点C,抛物线的对称轴交轴于点D,已知A(,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是等腰三角形?如果存在,请出P点的坐标;如果不存在,请说明理由;
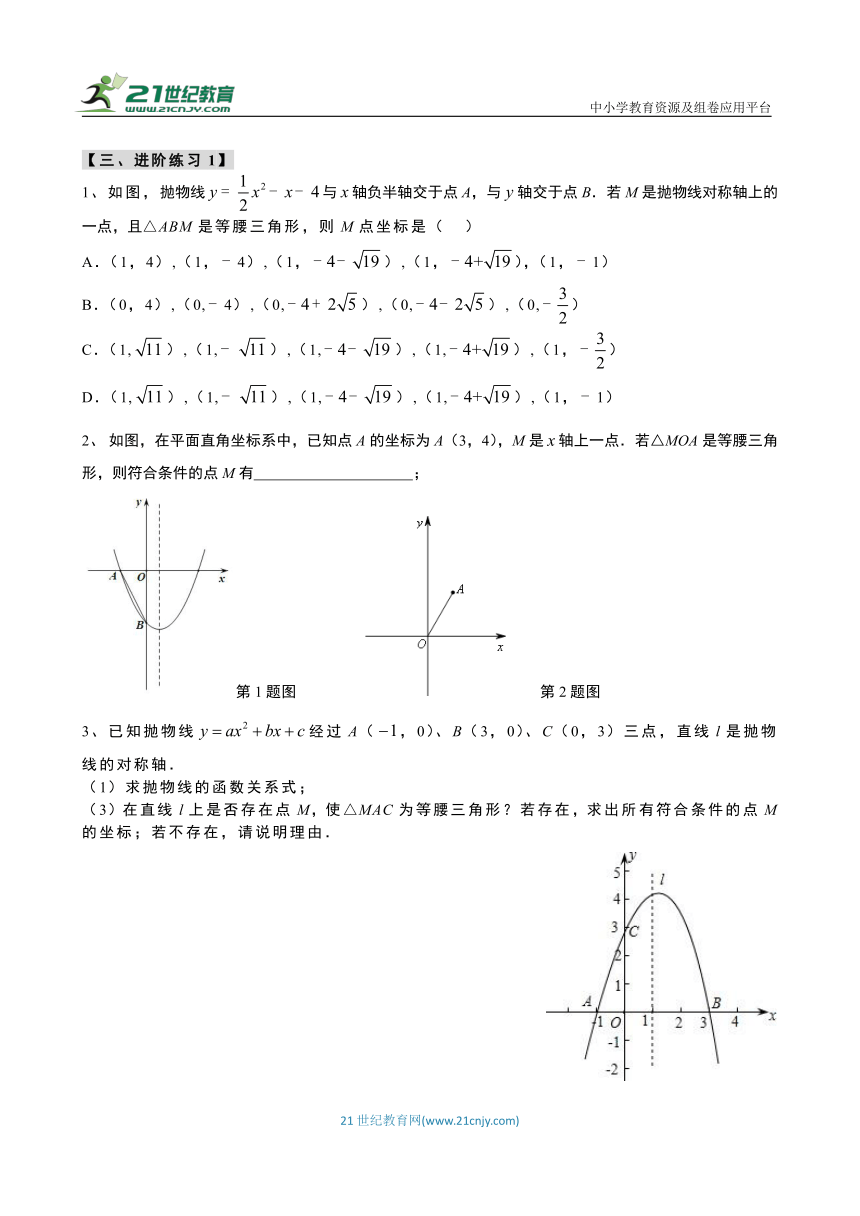
【三、进阶练习1】
1、如图,抛物线与轴负半轴交于点A,与轴交于点B.若M是抛物线对称轴上的一点,且△ABM是等腰三角形,则M点坐标是( )
A.(1,4),(1,4),(1,),(1,),(1,1)
B.(0,4),(0,4),(0,),(0,),(0,)
C.(1,),(1,),(1,),(1,),(1,)
D.(1,),(1,),(1,),(1,),(1,1)
2、 如图,在平面直角坐标系中,已知点A的坐标为A(3,4),M是轴上一点.若△MOA是等腰三角形,则符合条件的点M有 ;
第1题图 第2题图
3、已知抛物线经过A(,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
【三、进阶练习2】
1、如图,抛物线与轴负半轴交于点A,与轴交于点B.若M是抛物线对称轴上的一点,且△ABM为等腰三角形,则M点坐标为( )
A.(1,),(1,),(1,0),(1,),(1,1)
B.(1,),(1,),(1,0),(1,1),(0,)
C.(1,),(1,),(1,0),(1,),(1,)
D.(1,),(1,),(1,0),(1,1) 第1题图
2、如图,抛物线与轴的交于点C,点D(0,1),点P是抛物线上的一个动点.若△PCD是以CD为底的等腰三角形,则P点的坐标是 ;
第2题图
3、已知二次函数经过点A(,0)、C(0,3),与轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
【参考答案】
第2章《几何图形与函数专题》
第1课时 《等腰三角形存在性问题》
【例1】(1);(2),,,;
【进阶练习1】1、D; 2、,,,;
3、(1);(2),,,;
【进阶练习2】1、D; 2、,;
(1);
(2)当DC=DP时,; 当PC=PD时,; 当CD=CP时,不存在;
21世纪教育网(www.21cnjy.com)
第2章 几何图形与函数专题
第 1课时 等腰三角形存在性模型
【一、模型构建】
请在直线l上找一点P,使△PAB为等腰三角形:
【二、典型例题】
【例1】如图,抛物线与轴交于A、B两点,与轴交于点C,抛物线的对称轴交轴于点D,已知A(,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是等腰三角形?如果存在,请出P点的坐标;如果不存在,请说明理由;
【三、进阶练习1】
1、如图,抛物线与轴负半轴交于点A,与轴交于点B.若M是抛物线对称轴上的一点,且△ABM是等腰三角形,则M点坐标是( )
A.(1,4),(1,4),(1,),(1,),(1,1)
B.(0,4),(0,4),(0,),(0,),(0,)
C.(1,),(1,),(1,),(1,),(1,)
D.(1,),(1,),(1,),(1,),(1,1)
2、 如图,在平面直角坐标系中,已知点A的坐标为A(3,4),M是轴上一点.若△MOA是等腰三角形,则符合条件的点M有 ;
第1题图 第2题图
3、已知抛物线经过A(,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
【三、进阶练习2】
1、如图,抛物线与轴负半轴交于点A,与轴交于点B.若M是抛物线对称轴上的一点,且△ABM为等腰三角形,则M点坐标为( )
A.(1,),(1,),(1,0),(1,),(1,1)
B.(1,),(1,),(1,0),(1,1),(0,)
C.(1,),(1,),(1,0),(1,),(1,)
D.(1,),(1,),(1,0),(1,1) 第1题图
2、如图,抛物线与轴的交于点C,点D(0,1),点P是抛物线上的一个动点.若△PCD是以CD为底的等腰三角形,则P点的坐标是 ;
第2题图
3、已知二次函数经过点A(,0)、C(0,3),与轴交于另一点B,抛物线的顶点为D.
(1)求此二次函数解析式;
(2)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
【参考答案】
第2章《几何图形与函数专题》
第1课时 《等腰三角形存在性问题》
【例1】(1);(2),,,;
【进阶练习1】1、D; 2、,,,;
3、(1);(2),,,;
【进阶练习2】1、D; 2、,;
(1);
(2)当DC=DP时,; 当PC=PD时,; 当CD=CP时,不存在;
21世纪教育网(www.21cnjy.com)
同课章节目录
