人教版六年级下学期数学6.1.4比和比例课件(共15张PPT)
文档属性
| 名称 | 人教版六年级下学期数学6.1.4比和比例课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 22.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
比和比例
一、引入情境,回顾旧知
提问2:黑板上写了这么多的比,谁能再说一个比和黑板上的比,
组成比例?
监控:比值相等。
教师板书
监控问题:
①说的对吗?
②你是怎么判断的?
③判断的依据是什么?
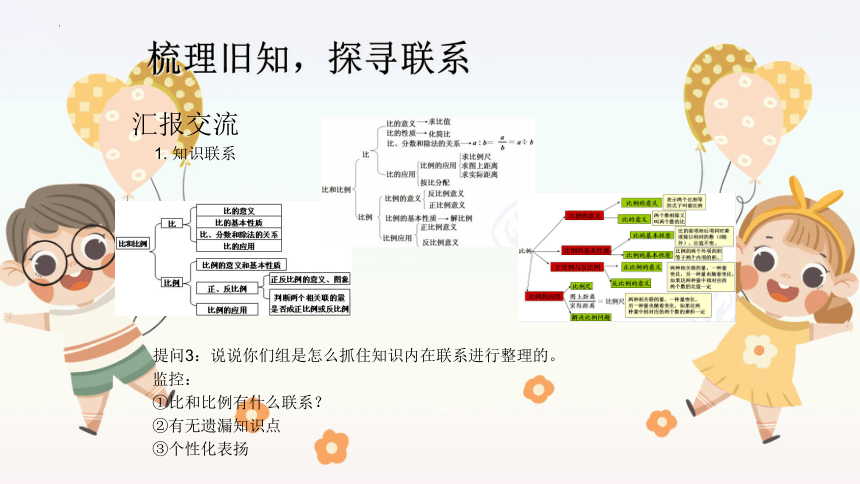
1. 知识联系
汇报交流
梳理旧知,探寻联系
监控:
①比和比例有什么联系?
②有无遗漏知识点
③个性化表扬
提问3:说说你们组是怎么抓住知识内在联系进行整理的。
正比例 反比例
相同点 不 同 点
都有一个不变量;两个变量,一种量随着另一种量变化。
xy=k(一定)
积一定
比值(商)一定
(一定)
正比例和反比例的相同点和不同点:
正比例图像是一条直线。
反比例图像是一条曲线。
找一找下面这题化简比对吗?该怎么改?
20m:50km
=(20÷10):(50÷10)
= 2:5
= 20m:50000m
= 1:2500
比的前项和后项是不同单位名数时,首先要把它们转化成相同单位名数,再利用比的基本性质转化成最简整数比。
×
20m:50km
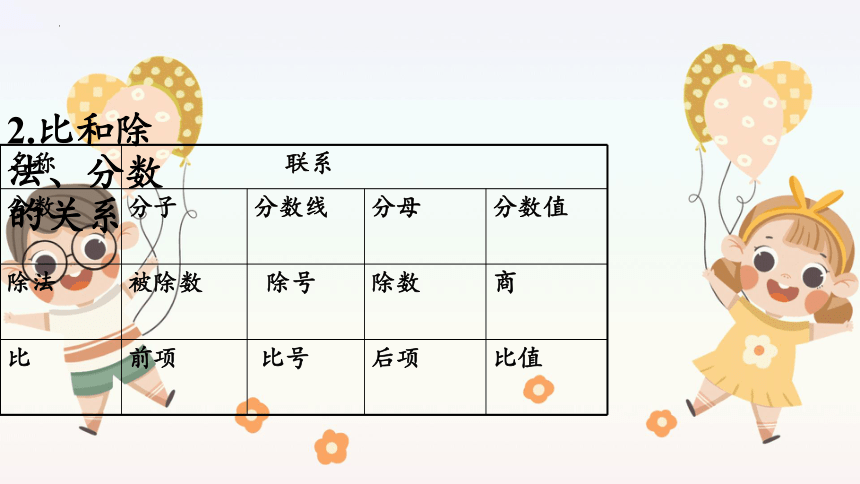
2.比和除法、分数的关系
名称 联系 分数 分子 分数线 分母 分数值
除法 被除数 除号 除数 商
比 前项 比号 后项 比值
我会填
1.把1g药放入100g水中,药和药水的比是( )。
2. :6的比值是( )。
如果前项乘3,要使比值不变,后项应该( )。
3.如果a×3=b×5,那么a:b=( ):( )
如果甲:乙=4:3,乙:丙=4:9,
则甲:乙:丙=( )
2
3
1:101
乘3或者 增加12
1
9
5
3
16:12:27
判断正反比例方法
一找二看三判断
(1)找变量:分析数量关系,确定两种量是否是相关联的量。
(2)看定量:分析这两种相关联的量,它们之间的关系是比值一定,
还是乘积一定。
(3)判断:如果比值一定,就成正比例关系;如果乘积一定,就成
反比例关系; 如果比值和乘积都不是定量,就不成比例
关系。
(1)甲车4小时行驶280km,乙车3小时行驶300km。
①甲车行驶的路程与时间的比是( )。
②乙车行驶的路程与时间的比是( )。
③乙车与甲车行驶的路程比是( )。
④甲车与乙车行驶的时间比是( )。
(2)如果n×4=m×7,那么n:m=( ):( )。
二、梳理旧知,探寻联系
出示练习:
拓展练习
观察下面各图,根据长方形的长与宽,探索长方形面积的关系,并解答。
(1)
甲
乙
a
b
左图中长方形甲与乙的( )相等,( )和( )成正比例关系。甲、乙的长之比是( ),面积比是( )。
(2)
甲
丙
c
d
左图中长方形甲与丙的( )相等。甲、丙的宽之比是( ),甲与丙的面积的比是( )。
(3)
甲
丙
c
d
乙
丁
a
b
若用S表示长方形的面积。S甲:S乙=( ), S丙:S丁=( ),S甲:S丙=( ), S乙:S丁=( )。
甲
丙
乙
丁
(4)
若S甲=18, S乙=8,S丙=12, 求S丁。
宽
面积
长
a:b
a:b
长
c:d
c:d
a:b
a:b
c:d
c:d
S甲:S乙=18:8=9:4
S丙:S丁=12:S丁=9:4
S丁=
1
3
5
面积÷长=宽(一定)
面积÷宽=长(一定)
1. 正比例和反比例的意义 用字母如何表示?
2.判断成正比例和反比例的方法
关于正比例和反比例你想说什么?
四.探索与交流
同一时间,同一地点测得树高和影长如下图:
(1)看图填写下表:
(2)树高和影长成比例吗?成什么比例?为什么?
(3)根据图象,估计8米高的树,这时的影长是多少米?
谢谢,请提出宝贵意见!
再见
比和比例
一、引入情境,回顾旧知
提问2:黑板上写了这么多的比,谁能再说一个比和黑板上的比,
组成比例?
监控:比值相等。
教师板书
监控问题:
①说的对吗?
②你是怎么判断的?
③判断的依据是什么?
1. 知识联系
汇报交流
梳理旧知,探寻联系
监控:
①比和比例有什么联系?
②有无遗漏知识点
③个性化表扬
提问3:说说你们组是怎么抓住知识内在联系进行整理的。
正比例 反比例
相同点 不 同 点
都有一个不变量;两个变量,一种量随着另一种量变化。
xy=k(一定)
积一定
比值(商)一定
(一定)
正比例和反比例的相同点和不同点:
正比例图像是一条直线。
反比例图像是一条曲线。
找一找下面这题化简比对吗?该怎么改?
20m:50km
=(20÷10):(50÷10)
= 2:5
= 20m:50000m
= 1:2500
比的前项和后项是不同单位名数时,首先要把它们转化成相同单位名数,再利用比的基本性质转化成最简整数比。
×
20m:50km
2.比和除法、分数的关系
名称 联系 分数 分子 分数线 分母 分数值
除法 被除数 除号 除数 商
比 前项 比号 后项 比值
我会填
1.把1g药放入100g水中,药和药水的比是( )。
2. :6的比值是( )。
如果前项乘3,要使比值不变,后项应该( )。
3.如果a×3=b×5,那么a:b=( ):( )
如果甲:乙=4:3,乙:丙=4:9,
则甲:乙:丙=( )
2
3
1:101
乘3或者 增加12
1
9
5
3
16:12:27
判断正反比例方法
一找二看三判断
(1)找变量:分析数量关系,确定两种量是否是相关联的量。
(2)看定量:分析这两种相关联的量,它们之间的关系是比值一定,
还是乘积一定。
(3)判断:如果比值一定,就成正比例关系;如果乘积一定,就成
反比例关系; 如果比值和乘积都不是定量,就不成比例
关系。
(1)甲车4小时行驶280km,乙车3小时行驶300km。
①甲车行驶的路程与时间的比是( )。
②乙车行驶的路程与时间的比是( )。
③乙车与甲车行驶的路程比是( )。
④甲车与乙车行驶的时间比是( )。
(2)如果n×4=m×7,那么n:m=( ):( )。
二、梳理旧知,探寻联系
出示练习:
拓展练习
观察下面各图,根据长方形的长与宽,探索长方形面积的关系,并解答。
(1)
甲
乙
a
b
左图中长方形甲与乙的( )相等,( )和( )成正比例关系。甲、乙的长之比是( ),面积比是( )。
(2)
甲
丙
c
d
左图中长方形甲与丙的( )相等。甲、丙的宽之比是( ),甲与丙的面积的比是( )。
(3)
甲
丙
c
d
乙
丁
a
b
若用S表示长方形的面积。S甲:S乙=( ), S丙:S丁=( ),S甲:S丙=( ), S乙:S丁=( )。
甲
丙
乙
丁
(4)
若S甲=18, S乙=8,S丙=12, 求S丁。
宽
面积
长
a:b
a:b
长
c:d
c:d
a:b
a:b
c:d
c:d
S甲:S乙=18:8=9:4
S丙:S丁=12:S丁=9:4
S丁=
1
3
5
面积÷长=宽(一定)
面积÷宽=长(一定)
1. 正比例和反比例的意义 用字母如何表示?
2.判断成正比例和反比例的方法
关于正比例和反比例你想说什么?
四.探索与交流
同一时间,同一地点测得树高和影长如下图:
(1)看图填写下表:
(2)树高和影长成比例吗?成什么比例?为什么?
(3)根据图象,估计8米高的树,这时的影长是多少米?
谢谢,请提出宝贵意见!
再见
