数学高中北师大版必修四2.4《平面向量的坐标》课件
文档属性
| 名称 | 数学高中北师大版必修四2.4《平面向量的坐标》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 348.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-11 20:35:59 | ||
图片预览


文档简介
课件17张PPT。4.1~4.2平面向量的坐标平面向量的坐标课题引入:1.在平面直角坐标系中,每个点都有一坐标与之对应
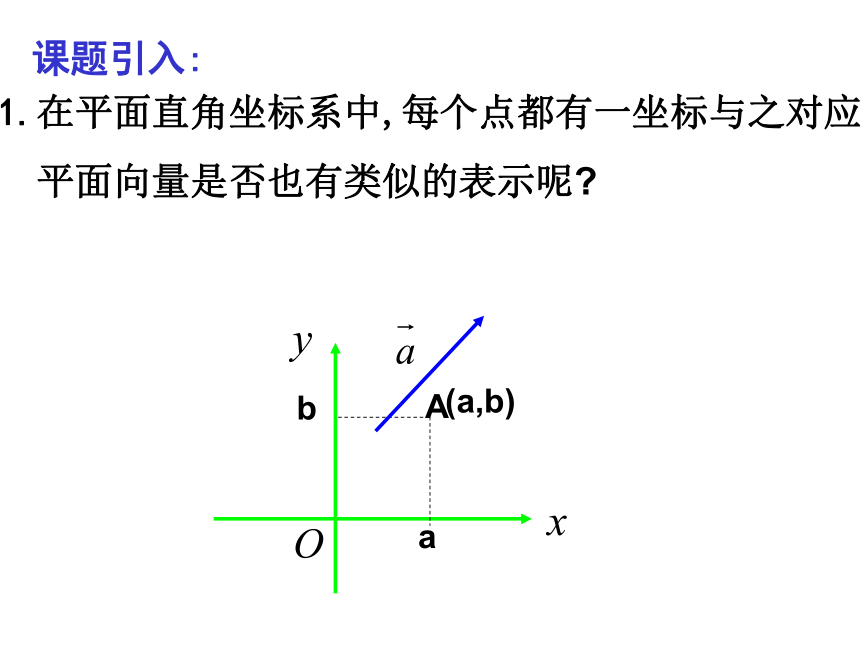
平面向量是否也有类似的表示呢?
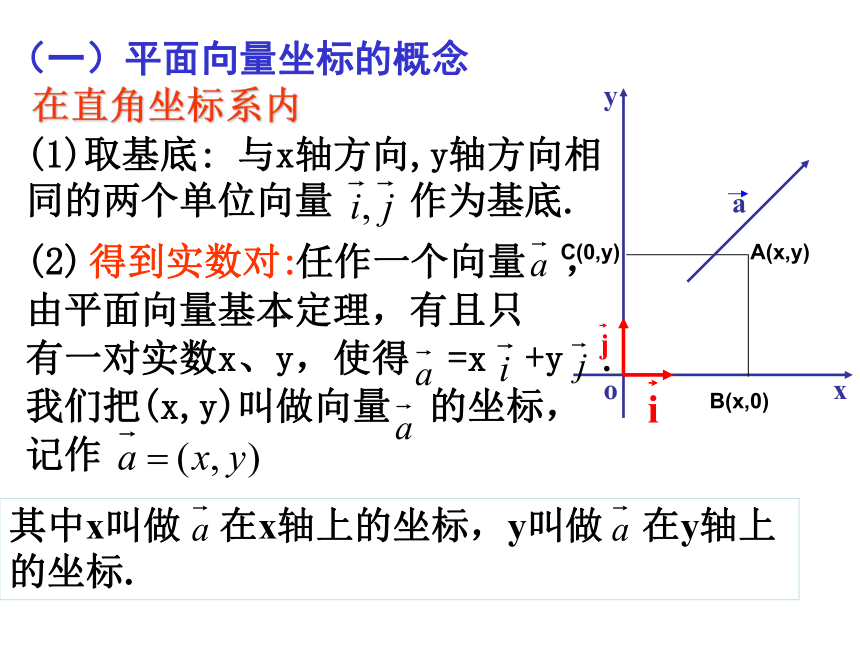
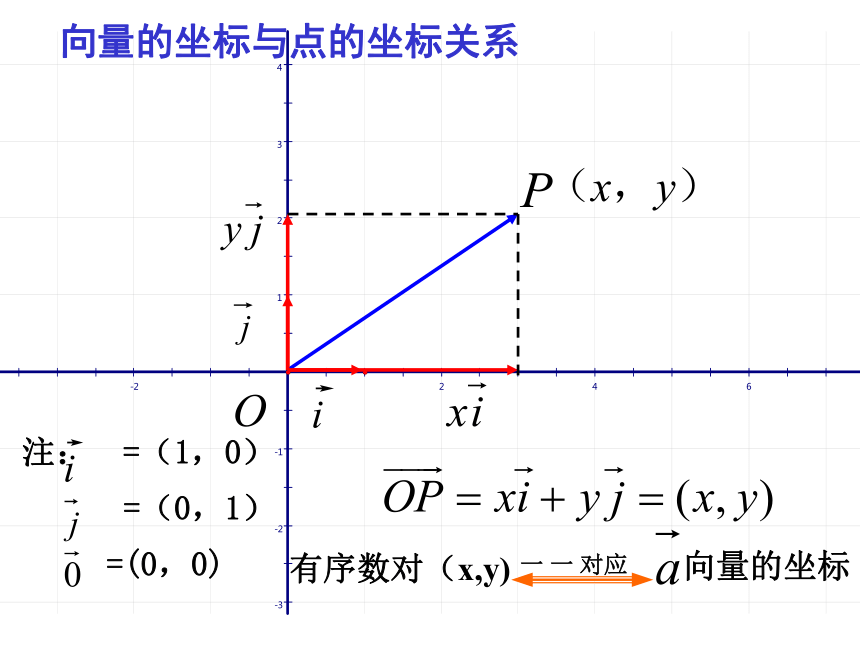
A(a,b)ab3.复习平面向量基本定理:什么叫平面的一组基底?平面的基底有多少组?无数组如果 是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 ,有且只有一对实数 λ1 , λ2 使得 = λ1 + λ2不共线的两向量 ,叫做这一平面内所有向量的一组基底.(一)平面向量坐标的概念在直角坐标系内(1)取基底: 与x轴方向,y轴方向相同的两个单位向量 作为基底.其中x叫做 在x轴上的坐标,y叫做 在y轴上的坐标.A(x,y)B(x,0)C(0,y)向量的坐标与点的坐标关系注: =(1,0)
=(0,1)
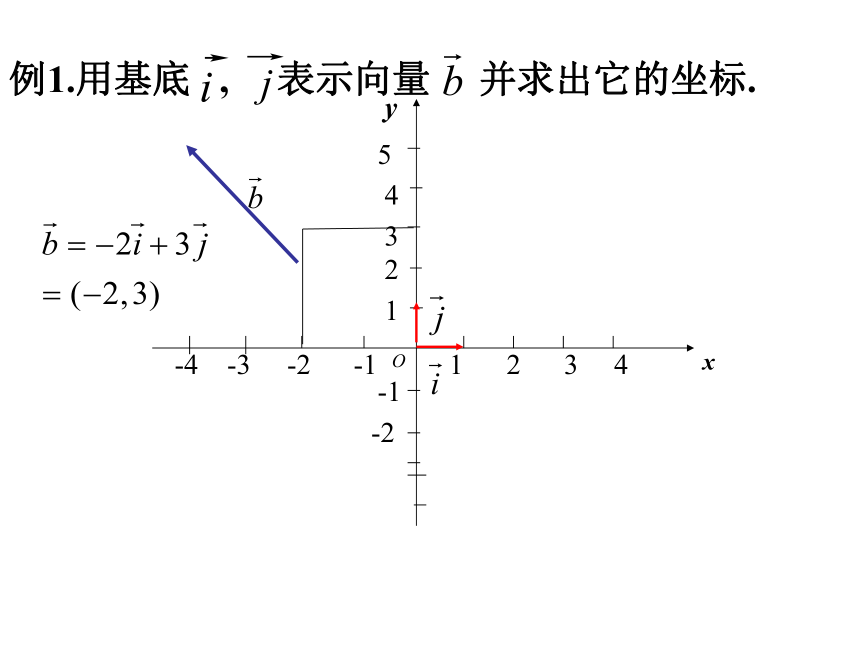
=(0,0)例1.用基底 , 表示向量 并求出它的坐标.-4 -3 -2 -1 1 2 3 412-2-1xy453注:对向量坐标表示的理解:(1)任一平面向量都有唯一的坐标与之对应。(3)相等的向量有相等的坐标.(2)起点在坐标原点的向量的坐标为其终点 的坐标。(二)平面向量的坐标运算:结论1:两个向量和与差的坐标分别等于这两个向量相应坐标的和与差.结论2:实数与向量数量积的坐标等于用这个实数乘原来向量的相应坐标.探究一例3 已知三个力 =(3, 4), =(2, ?5), =(x, y)的合力:++=,求的坐标。解:由题设 得:(3, 4)+ (2, ?5)+(x, y)=(0, 0)
即: ∴结论3:一个向量的坐标等于表示此向量的有向线段终点的坐标减去起点的坐标。 已知 ,求 的坐标. 探究二例5:已知平行四边形ABCD的三个顶点A、B、C的坐标分别为(-2,1)、(-1,3)、(3,4),求顶点D的坐标。xyOA(-2,1)B(-1,3)C(3,4)课堂小结:1.向量的坐标的概念:2.对向量坐标表示的理解:3.平面向量的坐标运算:(1)任一平面向量都有唯一的坐标;(2)相等的向量有相等的坐标.选做作业(例5变式):已知平面上三点的坐标分别为A(?2, 1), B(?1, 3), C(3, 4),求点D的坐标使这四点构成平行四边形四个顶点。ABC必做作业:习题2-4 A组 1,3,5布置作业:
平面向量是否也有类似的表示呢?
A(a,b)ab3.复习平面向量基本定理:什么叫平面的一组基底?平面的基底有多少组?无数组如果 是同一平面内的两个不共线的向量,那么对于这一平面内的任一向量 ,有且只有一对实数 λ1 , λ2 使得 = λ1 + λ2不共线的两向量 ,叫做这一平面内所有向量的一组基底.(一)平面向量坐标的概念在直角坐标系内(1)取基底: 与x轴方向,y轴方向相同的两个单位向量 作为基底.其中x叫做 在x轴上的坐标,y叫做 在y轴上的坐标.A(x,y)B(x,0)C(0,y)向量的坐标与点的坐标关系注: =(1,0)
=(0,1)
=(0,0)例1.用基底 , 表示向量 并求出它的坐标.-4 -3 -2 -1 1 2 3 412-2-1xy453注:对向量坐标表示的理解:(1)任一平面向量都有唯一的坐标与之对应。(3)相等的向量有相等的坐标.(2)起点在坐标原点的向量的坐标为其终点 的坐标。(二)平面向量的坐标运算:结论1:两个向量和与差的坐标分别等于这两个向量相应坐标的和与差.结论2:实数与向量数量积的坐标等于用这个实数乘原来向量的相应坐标.探究一例3 已知三个力 =(3, 4), =(2, ?5), =(x, y)的合力:++=,求的坐标。解:由题设 得:(3, 4)+ (2, ?5)+(x, y)=(0, 0)
即: ∴结论3:一个向量的坐标等于表示此向量的有向线段终点的坐标减去起点的坐标。 已知 ,求 的坐标. 探究二例5:已知平行四边形ABCD的三个顶点A、B、C的坐标分别为(-2,1)、(-1,3)、(3,4),求顶点D的坐标。xyOA(-2,1)B(-1,3)C(3,4)课堂小结:1.向量的坐标的概念:2.对向量坐标表示的理解:3.平面向量的坐标运算:(1)任一平面向量都有唯一的坐标;(2)相等的向量有相等的坐标.选做作业(例5变式):已知平面上三点的坐标分别为A(?2, 1), B(?1, 3), C(3, 4),求点D的坐标使这四点构成平行四边形四个顶点。ABC必做作业:习题2-4 A组 1,3,5布置作业:
