数学高中北师大版必修四《从力做的功到向量的数量积》课件
文档属性
| 名称 | 数学高中北师大版必修四《从力做的功到向量的数量积》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 38.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-11 00:00:00 | ||
图片预览





文档简介
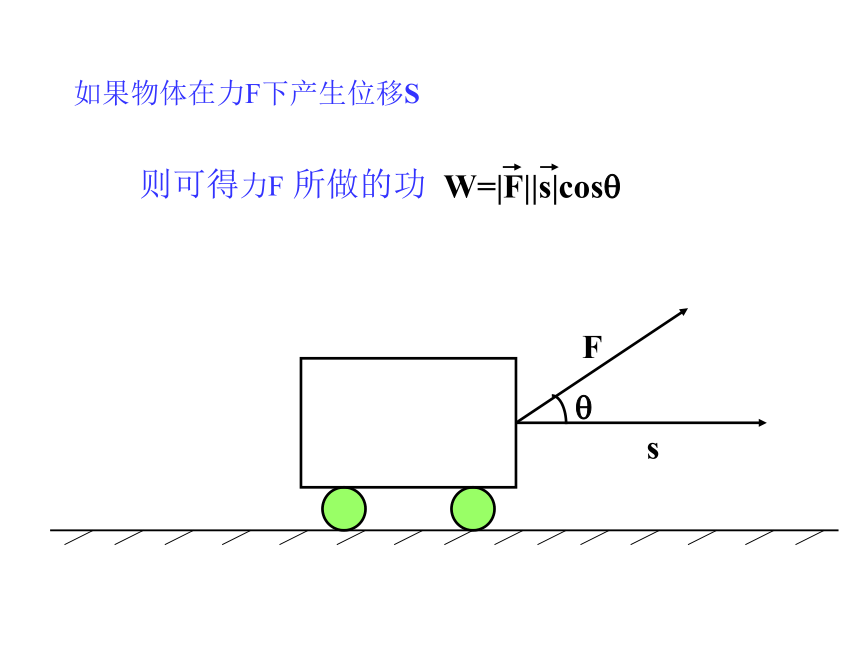
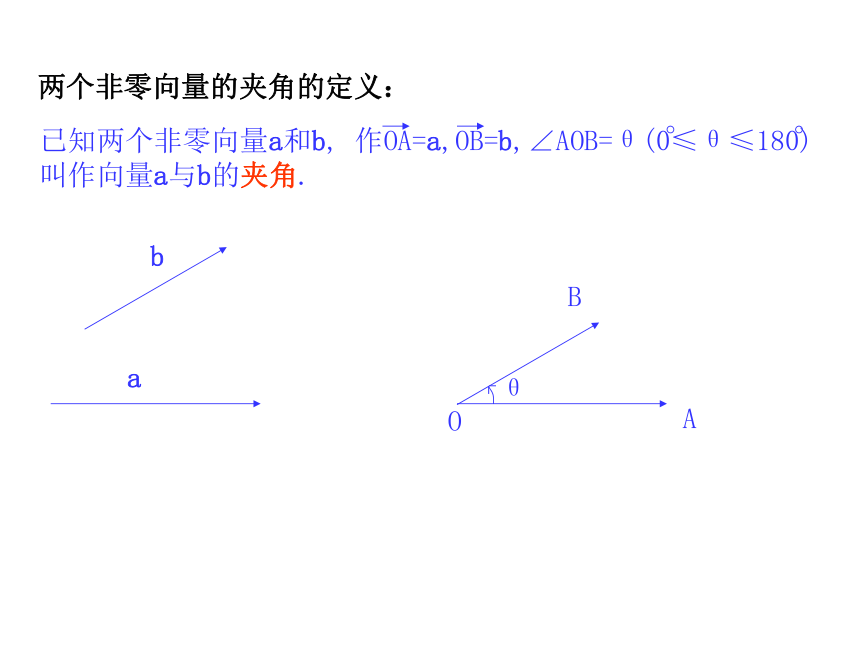
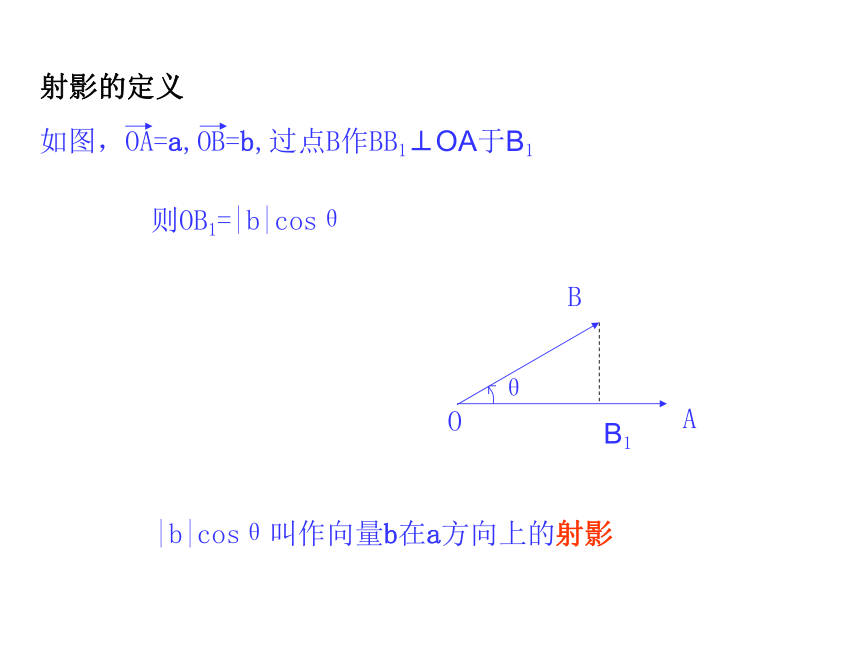
课件21张PPT。§5 从力做的功到向量的数量积如果物体在力F下产生位移S则可得力F 所做的功ab两个非零向量的夹角的定义: 我们规定零向量可与任一向量垂直.如图,OA=a,OB=b,过点B作BB1⊥OA于B1B1则OB1=|b|cosθ|b|cosθ叫作向量b在a方向上的射影射影的定义当θ为锐角时,|b|cosθ>0当θ为钝角时,|b|cosθ<0当θ为直角时,|b|cosθ=0已知两个非零向量a和b,它们的夹角为θ,我们把|a||b|cos θ叫作向量a和b的数量积(或内积).记作a·ba · b= |a| |b| cos θ向量的数量积的几何意义: 向量a与b的数量积等于a的长度|a|与b在a方向上射影|b|cosθ的乘积,或b的长度|b|与a在b方向上射影|a|cosθ的乘积.当两个向量相等时,两个向量的数量积等于向量长度的平方:当两个向量都是单位向量时,它们的数量积等于它们夹角的余弦值:向量的数量积的物理意义: 如果力对物体做功,就是力F与其作用下物体的位移s的数量积F·s.解 a·b= |a| |b|cosθ=3×4×cos150 例1 已知|a|=3,|b|=4,且a与b的夹角θ=150 ,求a·b例2 在三角形ABC,设边BC,CA,AB的长度分别为a,b,c,证明:a2=b2+c2-2bccosA
b2=c2+a2-2cacosB
c2=a2+b2-2abcosCABCabc同理可证其他二式.我们把这个结果称为余弦定理.证明 如图,设 ,则例3 证明菱形的两条对角线互相垂直.ABCDO证明 菱形ABCD中,AB=AD即菱形的两条对角线互相垂直.①例4 已知单位向量e1,e2的夹角为60 ,求向量a= e1+e2,
b=e2-2e1夹角.解 由单位向量e1,e2的夹角为60 ,得e1·e2 = 由① ②可得又 |a|2=|e1+e2|2=|e1|2+2 e1 · e2 +|e2|2=3 |b|2=|e2-2e1|2=4|e1|2-4 e1 · e2 +|e2|2=3②所以 |a|=|b|= 又0<θ<π,所以θ=120
(1)(5)若 ,则对于任一非零 有??(2)?(3)??(7)对于任意向量 都有?(6)若 ,则 至少有一个为判断下列命题是否正确:公式变形对功W=|F||s|cos?结构分析抽象平面向量数量积的定义a · b=| a | | b | cos ?特殊化五条重要性质数形结合几何意义小结(1)向量的数量积的定义(2)平面向量数量积的物理意义和几何意义小结(3)向量的数量积的性质(4)向量的数量积的运算律
b2=c2+a2-2cacosB
c2=a2+b2-2abcosCABCabc同理可证其他二式.我们把这个结果称为余弦定理.证明 如图,设 ,则例3 证明菱形的两条对角线互相垂直.ABCDO证明 菱形ABCD中,AB=AD即菱形的两条对角线互相垂直.①例4 已知单位向量e1,e2的夹角为60 ,求向量a= e1+e2,
b=e2-2e1夹角.解 由单位向量e1,e2的夹角为60 ,得e1·e2 = 由① ②可得又 |a|2=|e1+e2|2=|e1|2+2 e1 · e2 +|e2|2=3 |b|2=|e2-2e1|2=4|e1|2-4 e1 · e2 +|e2|2=3②所以 |a|=|b|= 又0<θ<π,所以θ=120
(1)(5)若 ,则对于任一非零 有??(2)?(3)??(7)对于任意向量 都有?(6)若 ,则 至少有一个为判断下列命题是否正确:公式变形对功W=|F||s|cos?结构分析抽象平面向量数量积的定义a · b=| a | | b | cos ?特殊化五条重要性质数形结合几何意义小结(1)向量的数量积的定义(2)平面向量数量积的物理意义和几何意义小结(3)向量的数量积的性质(4)向量的数量积的运算律
