数学高中北师大版必修四《平面向量的坐标》课件1
文档属性
| 名称 | 数学高中北师大版必修四《平面向量的坐标》课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 63.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-11 20:35:59 | ||
图片预览



文档简介
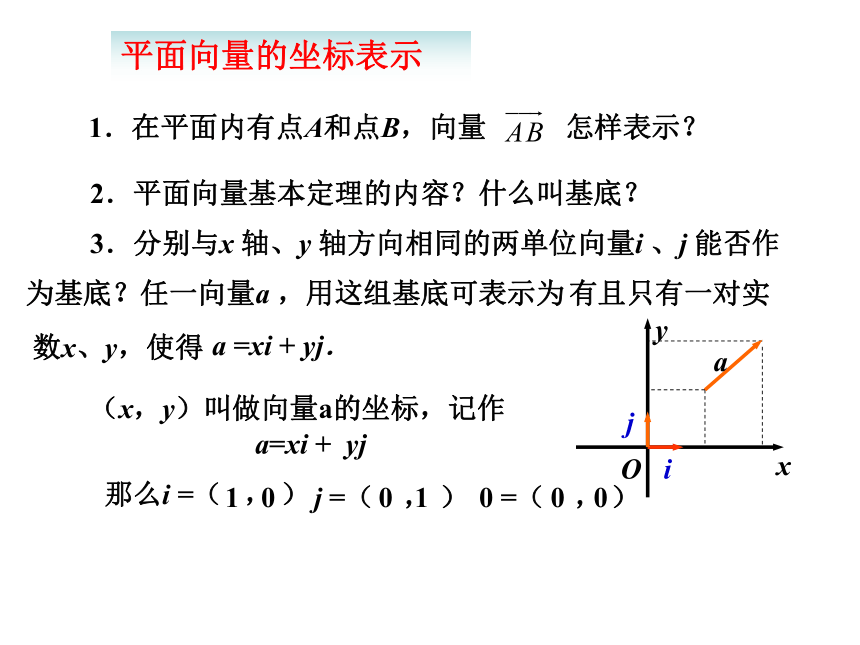
课件12张PPT。2.4 平面向量的坐标表示平面向量的坐标表示1.在平面内有点A和点B,向量 怎样表示?2.平面向量基本定理的内容?什么叫基底?1 00 10 0①向量的坐标与什么点的坐标有关?
②每一平面向量的坐标表示是否唯一的?
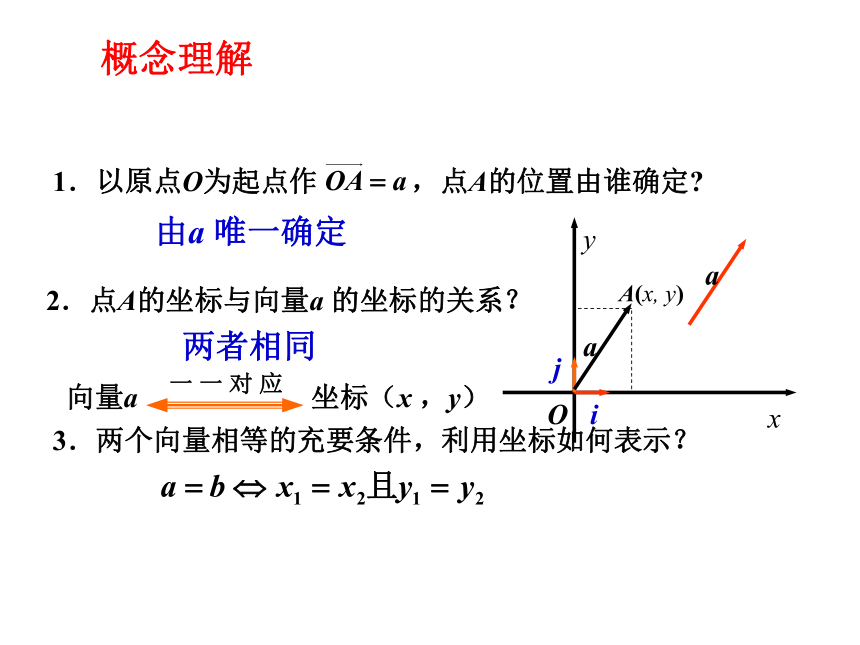
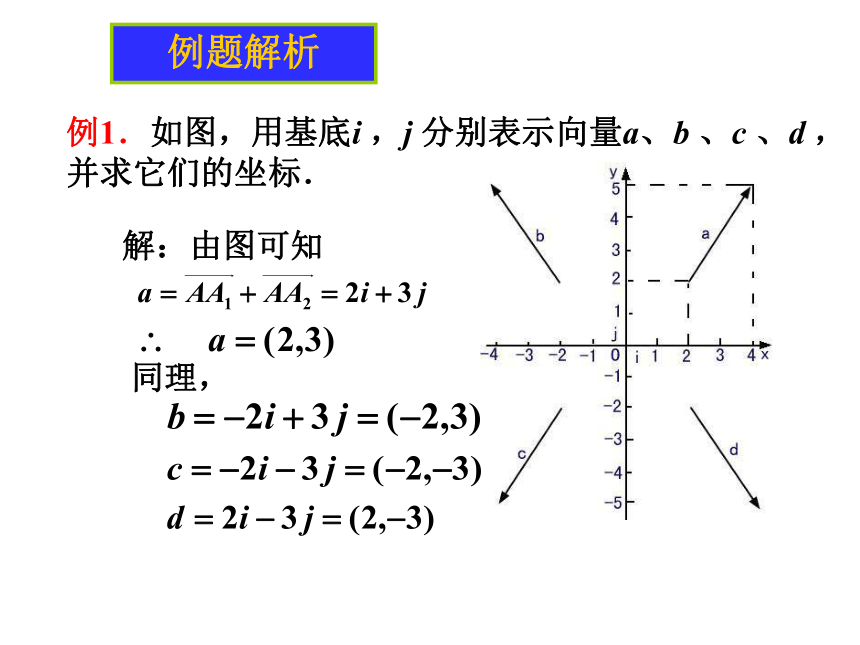
③两个向量相等的条件是?(两个向量坐标相等)学生讨论由a 唯一确定2.点A的坐标与向量a 的坐标的关系?两者相同概念理解3.两个向量相等的充要条件,利用坐标如何表示?例题解析例1.如图,用基底i ,j 分别表示向量a、b 、c 、d ,并求它们的坐标.解:由图可知同理,平面向量的坐标运算1.已知a ,b ,求a+b,a-b. a+b=( i + j ) + ( i + j )=( + )i+( + )j即同理可得两个向量和与差的坐标分别等于这两向量想应坐标的和与差解: 一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标. 实数与向量的积的坐标等于这个实数乘原来的向量的相应坐标.平面向量的坐标运算例题解析 例2.已知a=(2,1),b=(-3,4),求a+b,a-b,3a+4b的坐标.a-b=(2,1)-(-3,4)=(5,-3);3a+4b=3(2,1)+4(-3,4)
=(6,3)+(-12,16)
=(-6,19)例题解析解:设顶点D的坐标为(x,y) 例3. 已知 ABCD的三个顶点A、B、C的坐标分别为(-2,1)、( -1,3)、(3,4),求顶点D的坐标.1.若M(3, -2) N(-5, -1) 且 , 求P点的坐标;
解:设P(x, y) 则(x-3, y+2)= (-8, 1)=(-4, )
∴ ∴ ∴P点坐标为(-1, - )
2.若A(0, 1), B(1, 2), C(3, 4) 则?2=(-3,-3)
3.已知:四点A(5, 1), B(3, 4), C(1, 3), D(5, -3) 求证:四边形ABCD是梯形.
解:∵ =(-2, 3) =(-4, 6) ∴ =2
∴ ∥ 且 | | ? | | ∴四边形ABCD是梯形 巩固深化,发展思维[学习小结] (学生总结,其它学生补充)
①向量加法运算的坐标表示.
②向量减法运算的坐标表示.课堂小结作业:习题2——4 A组第1,2,3,4题 课后作业
②每一平面向量的坐标表示是否唯一的?
③两个向量相等的条件是?(两个向量坐标相等)学生讨论由a 唯一确定2.点A的坐标与向量a 的坐标的关系?两者相同概念理解3.两个向量相等的充要条件,利用坐标如何表示?例题解析例1.如图,用基底i ,j 分别表示向量a、b 、c 、d ,并求它们的坐标.解:由图可知同理,平面向量的坐标运算1.已知a ,b ,求a+b,a-b. a+b=( i + j ) + ( i + j )=( + )i+( + )j即同理可得两个向量和与差的坐标分别等于这两向量想应坐标的和与差解: 一个向量的坐标等于表示此向量的有向线段的终点的坐标减去始点的坐标. 实数与向量的积的坐标等于这个实数乘原来的向量的相应坐标.平面向量的坐标运算例题解析 例2.已知a=(2,1),b=(-3,4),求a+b,a-b,3a+4b的坐标.a-b=(2,1)-(-3,4)=(5,-3);3a+4b=3(2,1)+4(-3,4)
=(6,3)+(-12,16)
=(-6,19)例题解析解:设顶点D的坐标为(x,y) 例3. 已知 ABCD的三个顶点A、B、C的坐标分别为(-2,1)、( -1,3)、(3,4),求顶点D的坐标.1.若M(3, -2) N(-5, -1) 且 , 求P点的坐标;
解:设P(x, y) 则(x-3, y+2)= (-8, 1)=(-4, )
∴ ∴ ∴P点坐标为(-1, - )
2.若A(0, 1), B(1, 2), C(3, 4) 则?2=(-3,-3)
3.已知:四点A(5, 1), B(3, 4), C(1, 3), D(5, -3) 求证:四边形ABCD是梯形.
解:∵ =(-2, 3) =(-4, 6) ∴ =2
∴ ∥ 且 | | ? | | ∴四边形ABCD是梯形 巩固深化,发展思维[学习小结] (学生总结,其它学生补充)
①向量加法运算的坐标表示.
②向量减法运算的坐标表示.课堂小结作业:习题2——4 A组第1,2,3,4题 课后作业
