第九章统计小结复习课课件——2021-2022学年高一下学期数学人教A版(2019)必修第二册 (共19张PPT)
文档属性
| 名称 | 第九章统计小结复习课课件——2021-2022学年高一下学期数学人教A版(2019)必修第二册 (共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 09:51:54 | ||
图片预览




文档简介
(共19张PPT)
第九章小结
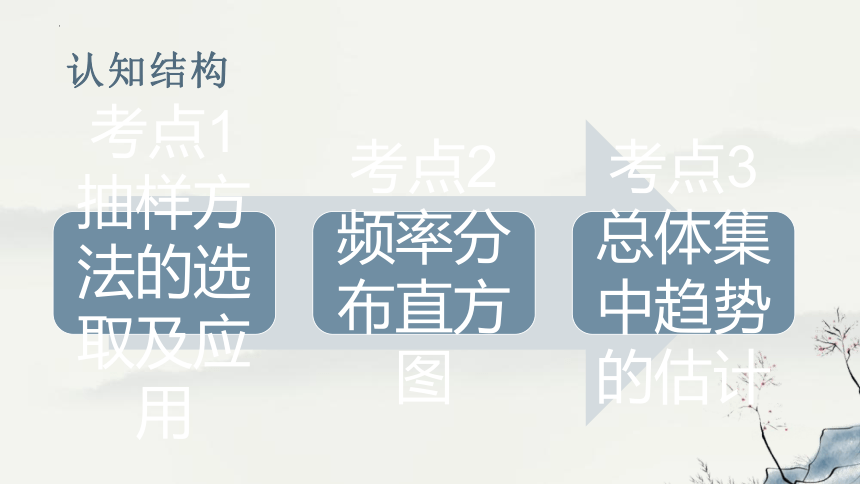
认知结构
考点1抽样方法的选取及应用
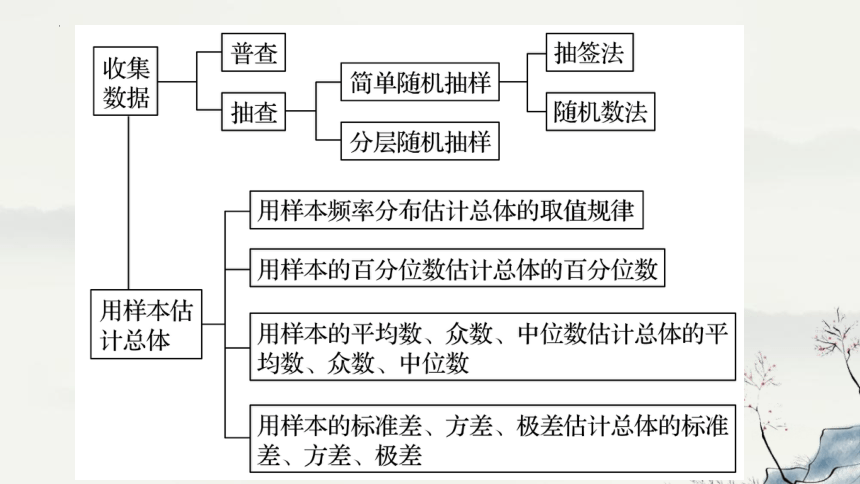
1.两种抽样方法的适用范围:
(1)当总体容量较小,样本容量也较小时,可采用抽签法;
(2)当总体容量较大,样本容量较小时,可采用随机数法;
(3)当总体中个体差异较显著时,可采用分层随机抽样.
【例1】(2017江苏高考)
某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取 件.
考点2 频率分布直方图
1.根据样本容量的大小,我们可以选择利用样本的频率分布表、频率分布直方图、频率折线图对总体情况作出估计.
2.掌握频率分布直方图的绘制及应用
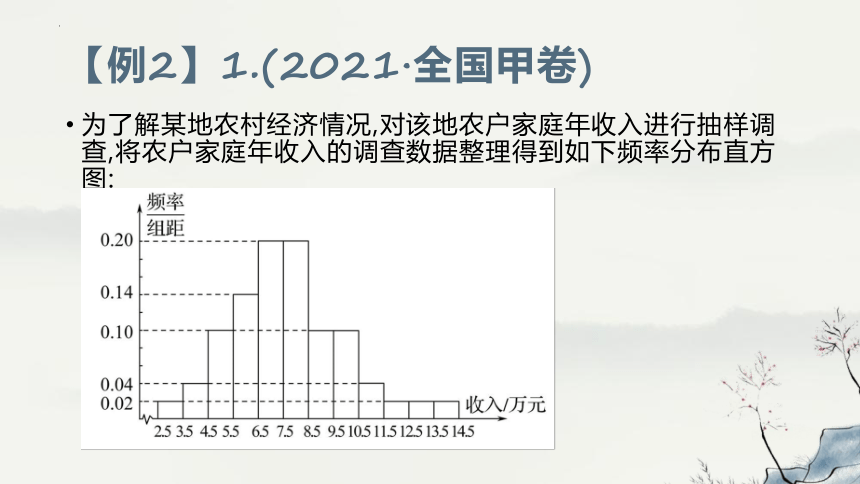
【例2】1.(2021·全国甲卷)
为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图,下面结论中不正确的是 ( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
【解析】
低于4.5万元的比率估计为0.02×1+0.04×1=0.06=6%,故A正确;
不低于10.5万元的比率估计为(0.04+0.02×3)×1=0.1=10%,故B正确;
平均值为:
(3×0.02+4×0.04+5×0.1+6×0.14+7×0.2+8×0.2+9×0.1+10×0.1+11×0.04+12×0.02+13×0.02+14×0.02)×1=7.68万元,故C不正确;
4.5万元到8.5万元的比率为:0.1×1+0.14×1+0.2×1+0.2×1=0.64=64%,故D正确.
A.10
B.18
C.20
D.36
考点3 总体集中趋势的估计
1.为了从整体上更好地把握总体的规律,我们可以通过样本数据的众数、中位数、平均数和标准差等数字特征对总体的数字特征作出估计;用方差s2反映样本数据分散程度的大小.
2.掌握样本数据的众数、中位数、平均数及方差的计算方法,提升数据分析和数学运算素养.
解析:由标准差的定义可知,标准差考察的是数据的离散程度;由中位数的定义可知,中位数考察的是数据的集中趋势;由极差的定义可知,极差考察的是数据的离散程度;由平均数的定义可知,平均数考察的是数据的集中趋势.
谢谢
第九章小结
认知结构
考点1抽样方法的选取及应用
1.两种抽样方法的适用范围:
(1)当总体容量较小,样本容量也较小时,可采用抽签法;
(2)当总体容量较大,样本容量较小时,可采用随机数法;
(3)当总体中个体差异较显著时,可采用分层随机抽样.
【例1】(2017江苏高考)
某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取 件.
考点2 频率分布直方图
1.根据样本容量的大小,我们可以选择利用样本的频率分布表、频率分布直方图、频率折线图对总体情况作出估计.
2.掌握频率分布直方图的绘制及应用
【例2】1.(2021·全国甲卷)
为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图,下面结论中不正确的是 ( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
【解析】
低于4.5万元的比率估计为0.02×1+0.04×1=0.06=6%,故A正确;
不低于10.5万元的比率估计为(0.04+0.02×3)×1=0.1=10%,故B正确;
平均值为:
(3×0.02+4×0.04+5×0.1+6×0.14+7×0.2+8×0.2+9×0.1+10×0.1+11×0.04+12×0.02+13×0.02+14×0.02)×1=7.68万元,故C不正确;
4.5万元到8.5万元的比率为:0.1×1+0.14×1+0.2×1+0.2×1=0.64=64%,故D正确.
A.10
B.18
C.20
D.36
考点3 总体集中趋势的估计
1.为了从整体上更好地把握总体的规律,我们可以通过样本数据的众数、中位数、平均数和标准差等数字特征对总体的数字特征作出估计;用方差s2反映样本数据分散程度的大小.
2.掌握样本数据的众数、中位数、平均数及方差的计算方法,提升数据分析和数学运算素养.
解析:由标准差的定义可知,标准差考察的是数据的离散程度;由中位数的定义可知,中位数考察的是数据的集中趋势;由极差的定义可知,极差考察的是数据的离散程度;由平均数的定义可知,平均数考察的是数据的集中趋势.
谢谢
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
