苏教版六年级下册数学 圆柱和圆锥 整理与练习 课件(29张PPT)
文档属性
| 名称 | 苏教版六年级下册数学 圆柱和圆锥 整理与练习 课件(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 24.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 16:54:36 | ||
图片预览





文档简介
(共29张PPT)
圆柱和圆锥整理与练习
义务教育教科书数学六年级下册
学
习
准
备
请准备好:
铅笔
橡皮
直尺
数学书
练习本
圆柱和圆锥整理与练习
关于圆柱和圆锥,我们学习了哪些知识
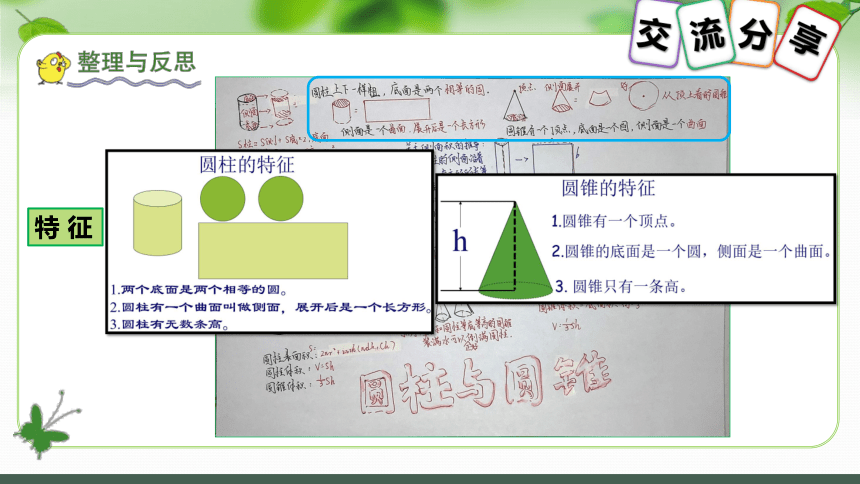
圆柱和圆锥的特征
圆柱表面积的计算
圆柱和圆锥体积的计算
回
顾
梳
理
课
前
梳
理
课
前
梳
理
特 征
交
流
分
享
特 征
交
流
分
享
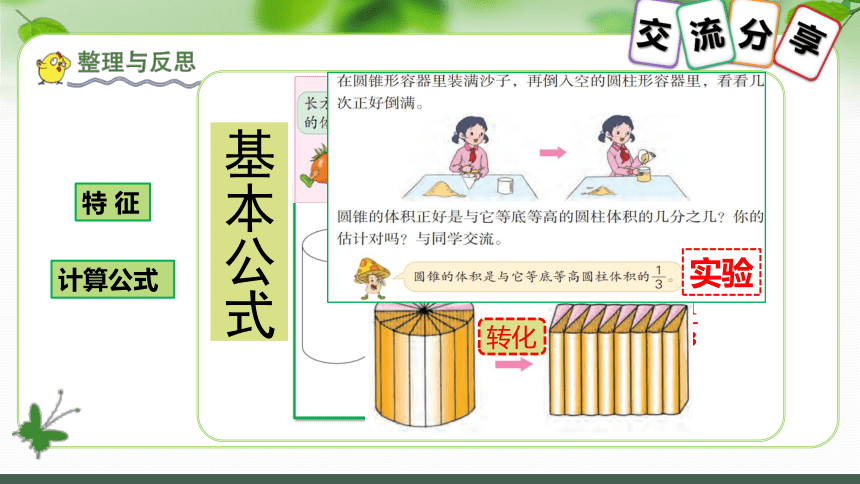
计算公式
基本公式
圆柱侧面积=
圆柱表面积=
圆柱体积=
圆锥体积=
底面周长×高
侧面积+底面积× 2
底面积×高
底面积×高×
V= s h
1
3
V = s h
S=πr
长=底面周长
宽= 高
转化
实验
交
流
分
享
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
沿着底面直径把这个圆柱切开,表面积增加了多少?
纵切
横切
3×2
×2
=12(平方分米)
答:表面积增加了12平方分米。
如果横切一次,表面积增加了多少?
增加2个长方形面积
横切一次,增加2个底面积
π×(2÷2) ×2=2π(平方分米)
答:表面积增加了2π平方分米。
切
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
把这个圆柱竖着放在地面,它的占地面积是多少?
底面积
π ×(2÷2) = π(平方分米)
答:它的占地面积是π平方分米。
把这个圆柱横着放,滚一圈的面积是多少?
侧面积
π ×2×3=6 π (平方分米)
答:滚一圈的面积是6π平方分米。
生活应用:
压路机问题
滚
巩
固
练
习
π ×0.8×1.6=1.28 π(平方米)
答:压路的面积是1.28 π平方米。
压路的面积
求侧面积
商标纸的面积
通风管用料的面积
烟囱用料的面积
刷柱子的面积
……
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
给这根木桩刷油漆,刷油漆的面积是多少?
①这根木桩全刷上油漆,刷油漆的面积是多少?
侧面积+底面积×2
π ×2×3+ π ×(2÷2) ×2=6 π +2 π =8 π (平方分米)
②贴着地面的底面不刷,
刷油漆的面积就是侧面积+一个底面积。
③这根木桩做柱子,
刷油漆的面积就是侧面积。
刷
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
切
滚
刷
这根木桩的体积是多少立方分米?
π ×(2÷2)
V=s h
×3
= 3π (立方分米)
答:这根木桩的体积是3 π立方分米。
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
切
滚
刷
把这根圆柱形的木桩削成最大的圆锥形,这个圆锥的体积是多少?
π ×(2÷2) ×3×
= π (立方分米)
答:这个圆锥的体积是π立方分米。
削
等底等高
圆锥的体积是圆柱体积的
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
切
滚
刷
把这个圆柱形的木桩削成最大的圆锥形,削去部分的体积是多少?
②π ×(2÷2) ×3×= =2 π ( dm )
答:削去部分的体积是2π立方分米。
削
①π ×(2÷2) ×3 - π ×(2÷2) ×3×=2 π (dm )
③π ×(2÷2) ×3×= =2 π ( dm )
圆锥体积:1份
圆柱体积:3份
削去部分体积:2份
一根圆柱形木桩,把它削成一个最大的圆锥,那么圆锥的体积是圆柱体积的( ),削去部分的体积是圆柱体积的( )。
等底等高的圆柱和圆锥体积之间的关系
圆锥的体积是与它等底等高圆柱体积的 ,
圆柱的体积是与它等底等高圆锥体积的3倍。
巩
固
练
习
(1)9个完全一样的圆锥形铁块,可以熔铸成与它等底等高的圆柱( )个。
(2)一个圆柱与一个圆锥等底等高,圆柱的体积比圆锥的体积大36立方分米,圆柱的体积是( )立方分米, 圆锥的体积是( )立方分米。
3
54
18
圆锥的体积是与它等底等高圆柱体积的 ,
圆柱的体积是与它等底等高圆锥体积的3倍。
关系
圆锥体积:1份
圆柱体积:3份
相差体积:2份
36立方分米
36÷2=18(dm )
18×3=54(dm )
巩
固
练
习
一块圆柱形橡皮泥,底面积是12平方厘米,高是5厘米,如果把它捏成底面积是12平方厘米的圆锥形,高是多少厘米?
把圆柱形橡皮泥捏成圆锥形,什么变了?什么没变?
形状变了,体积不变。
圆柱的体积
=圆锥的体积
12×5=60(cm )
圆锥的高=圆锥的体积×3÷底面积
60×3÷12=180÷12=15(cm)
圆锥和圆柱体积相等,底面积也相等,
它们的高有怎样的关系?
圆锥的高是圆柱高的3倍,圆柱的高是圆锥高的
5×3=15(cm)
一个圆柱和圆锥高相等,体积也相等,圆锥的底面积是12平方分米,那么圆柱的底面积是( )平方分米。
巩
固
练
习
圆锥和圆柱体积相等,高也相等,圆锥的底面积是圆柱底面积的3倍,圆柱的底面积是圆锥底面积的
12×=4(dm )
4
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
切
滚
刷
削
回
顾
小
结
巩
固
练
习
一张长方形纸片,长20厘米,宽10厘米,将它沿一边旋转一周后得到( )形状。
圆柱体
这个圆柱体的体积是多少?
沿着宽旋转一周形成圆柱
10厘米
20厘米
r=20厘米
h=10厘米
V=s h
π ×20 ×10
= 4000 π(cm )
10厘米
20厘米
沿着长旋转一周形成圆柱
r=10厘米
h=20厘米
V=s h
π ×10 ×20
= 2000 π(cm )
长方形沿着宽(沿着短边)旋转一周,形成的圆柱体积比较大。
回
顾
小
结
平面图形:长方形
立体图形:圆柱
旋转
平面图形:?
立体图形:圆锥
旋转
直角三角形
3cm
4cm
一个直角三角形,两条直角边分别是4cm、3cm,你觉得沿哪条直角边旋转一周,形成的圆锥体积比较大?
巩
固
练
习
沿着长直角边旋转一周形成圆锥
V= s h
π ×3 ×4×
= π×9 ×4×
=12 π (cm )
r=3cm
h=4cm
3cm
4cm
沿着短直角边旋转一周形成圆锥
V= s h
π ×4 ×3×
= π×16×3×
=16 π (cm )
r=4cm
h=3cm
直角三角形沿着短直角边旋转一周形成的圆锥体积比较大。
回
顾
小
结
解决这两个问题,你有什么收获
回
顾
小
结
平面图形
立体图形
旋转
长方形
圆柱
直角三角形
圆锥
长方形
旋转
圆柱
圆柱
?
卷
巩
固
练
习
巩
固
练
习
一张长方形纸片,长20厘米,宽10厘米,将它卷成一个圆柱,请想一想可以怎样卷?
宽10厘米
长20厘米
底面周长20厘米
高10厘米
计算卷成的圆柱的体积。(除不尽保留一位小数)
长20厘米
宽10厘米
底面周长10厘米
高20厘米
卷成的这两个圆柱的侧面积相等
r: 20÷π÷2≈3.2(cm)
V:π×3.2 ×10=102.4π(cm )
r: 10÷π÷2≈1.6(cm)
V:π×1.6 ×20=51.2π(cm )
长方形以长边为底面周长,短边为高,卷成的圆柱体积比较大。
回
顾
总
结
全课小结
通过今天的学习,你有哪些收获?
回
顾
总
结
圆柱和圆锥
同学们,再见!
圆柱和圆锥整理与练习
义务教育教科书数学六年级下册
学
习
准
备
请准备好:
铅笔
橡皮
直尺
数学书
练习本
圆柱和圆锥整理与练习
关于圆柱和圆锥,我们学习了哪些知识
圆柱和圆锥的特征
圆柱表面积的计算
圆柱和圆锥体积的计算
回
顾
梳
理
课
前
梳
理
课
前
梳
理
特 征
交
流
分
享
特 征
交
流
分
享
计算公式
基本公式
圆柱侧面积=
圆柱表面积=
圆柱体积=
圆锥体积=
底面周长×高
侧面积+底面积× 2
底面积×高
底面积×高×
V= s h
1
3
V = s h
S=πr
长=底面周长
宽= 高
转化
实验
交
流
分
享
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
沿着底面直径把这个圆柱切开,表面积增加了多少?
纵切
横切
3×2
×2
=12(平方分米)
答:表面积增加了12平方分米。
如果横切一次,表面积增加了多少?
增加2个长方形面积
横切一次,增加2个底面积
π×(2÷2) ×2=2π(平方分米)
答:表面积增加了2π平方分米。
切
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
把这个圆柱竖着放在地面,它的占地面积是多少?
底面积
π ×(2÷2) = π(平方分米)
答:它的占地面积是π平方分米。
把这个圆柱横着放,滚一圈的面积是多少?
侧面积
π ×2×3=6 π (平方分米)
答:滚一圈的面积是6π平方分米。
生活应用:
压路机问题
滚
巩
固
练
习
π ×0.8×1.6=1.28 π(平方米)
答:压路的面积是1.28 π平方米。
压路的面积
求侧面积
商标纸的面积
通风管用料的面积
烟囱用料的面积
刷柱子的面积
……
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
给这根木桩刷油漆,刷油漆的面积是多少?
①这根木桩全刷上油漆,刷油漆的面积是多少?
侧面积+底面积×2
π ×2×3+ π ×(2÷2) ×2=6 π +2 π =8 π (平方分米)
②贴着地面的底面不刷,
刷油漆的面积就是侧面积+一个底面积。
③这根木桩做柱子,
刷油漆的面积就是侧面积。
刷
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
切
滚
刷
这根木桩的体积是多少立方分米?
π ×(2÷2)
V=s h
×3
= 3π (立方分米)
答:这根木桩的体积是3 π立方分米。
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
切
滚
刷
把这根圆柱形的木桩削成最大的圆锥形,这个圆锥的体积是多少?
π ×(2÷2) ×3×
= π (立方分米)
答:这个圆锥的体积是π立方分米。
削
等底等高
圆锥的体积是圆柱体积的
巩
固
练
习
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
切
滚
刷
把这个圆柱形的木桩削成最大的圆锥形,削去部分的体积是多少?
②π ×(2÷2) ×3×= =2 π ( dm )
答:削去部分的体积是2π立方分米。
削
①π ×(2÷2) ×3 - π ×(2÷2) ×3×=2 π (dm )
③π ×(2÷2) ×3×= =2 π ( dm )
圆锥体积:1份
圆柱体积:3份
削去部分体积:2份
一根圆柱形木桩,把它削成一个最大的圆锥,那么圆锥的体积是圆柱体积的( ),削去部分的体积是圆柱体积的( )。
等底等高的圆柱和圆锥体积之间的关系
圆锥的体积是与它等底等高圆柱体积的 ,
圆柱的体积是与它等底等高圆锥体积的3倍。
巩
固
练
习
(1)9个完全一样的圆锥形铁块,可以熔铸成与它等底等高的圆柱( )个。
(2)一个圆柱与一个圆锥等底等高,圆柱的体积比圆锥的体积大36立方分米,圆柱的体积是( )立方分米, 圆锥的体积是( )立方分米。
3
54
18
圆锥的体积是与它等底等高圆柱体积的 ,
圆柱的体积是与它等底等高圆锥体积的3倍。
关系
圆锥体积:1份
圆柱体积:3份
相差体积:2份
36立方分米
36÷2=18(dm )
18×3=54(dm )
巩
固
练
习
一块圆柱形橡皮泥,底面积是12平方厘米,高是5厘米,如果把它捏成底面积是12平方厘米的圆锥形,高是多少厘米?
把圆柱形橡皮泥捏成圆锥形,什么变了?什么没变?
形状变了,体积不变。
圆柱的体积
=圆锥的体积
12×5=60(cm )
圆锥的高=圆锥的体积×3÷底面积
60×3÷12=180÷12=15(cm)
圆锥和圆柱体积相等,底面积也相等,
它们的高有怎样的关系?
圆锥的高是圆柱高的3倍,圆柱的高是圆锥高的
5×3=15(cm)
一个圆柱和圆锥高相等,体积也相等,圆锥的底面积是12平方分米,那么圆柱的底面积是( )平方分米。
巩
固
练
习
圆锥和圆柱体积相等,高也相等,圆锥的底面积是圆柱底面积的3倍,圆柱的底面积是圆锥底面积的
12×=4(dm )
4
结合圆柱和圆锥的有关知识以及我们的生活实际,展开想象的翅膀,请你提出数学问题。
切
滚
刷
削
回
顾
小
结
巩
固
练
习
一张长方形纸片,长20厘米,宽10厘米,将它沿一边旋转一周后得到( )形状。
圆柱体
这个圆柱体的体积是多少?
沿着宽旋转一周形成圆柱
10厘米
20厘米
r=20厘米
h=10厘米
V=s h
π ×20 ×10
= 4000 π(cm )
10厘米
20厘米
沿着长旋转一周形成圆柱
r=10厘米
h=20厘米
V=s h
π ×10 ×20
= 2000 π(cm )
长方形沿着宽(沿着短边)旋转一周,形成的圆柱体积比较大。
回
顾
小
结
平面图形:长方形
立体图形:圆柱
旋转
平面图形:?
立体图形:圆锥
旋转
直角三角形
3cm
4cm
一个直角三角形,两条直角边分别是4cm、3cm,你觉得沿哪条直角边旋转一周,形成的圆锥体积比较大?
巩
固
练
习
沿着长直角边旋转一周形成圆锥
V= s h
π ×3 ×4×
= π×9 ×4×
=12 π (cm )
r=3cm
h=4cm
3cm
4cm
沿着短直角边旋转一周形成圆锥
V= s h
π ×4 ×3×
= π×16×3×
=16 π (cm )
r=4cm
h=3cm
直角三角形沿着短直角边旋转一周形成的圆锥体积比较大。
回
顾
小
结
解决这两个问题,你有什么收获
回
顾
小
结
平面图形
立体图形
旋转
长方形
圆柱
直角三角形
圆锥
长方形
旋转
圆柱
圆柱
?
卷
巩
固
练
习
巩
固
练
习
一张长方形纸片,长20厘米,宽10厘米,将它卷成一个圆柱,请想一想可以怎样卷?
宽10厘米
长20厘米
底面周长20厘米
高10厘米
计算卷成的圆柱的体积。(除不尽保留一位小数)
长20厘米
宽10厘米
底面周长10厘米
高20厘米
卷成的这两个圆柱的侧面积相等
r: 20÷π÷2≈3.2(cm)
V:π×3.2 ×10=102.4π(cm )
r: 10÷π÷2≈1.6(cm)
V:π×1.6 ×20=51.2π(cm )
长方形以长边为底面周长,短边为高,卷成的圆柱体积比较大。
回
顾
总
结
全课小结
通过今天的学习,你有哪些收获?
回
顾
总
结
圆柱和圆锥
同学们,再见!
