数学高中北师大版必修四2.1《从位移、速度、力到向量》课件2
文档属性
| 名称 | 数学高中北师大版必修四2.1《从位移、速度、力到向量》课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 115.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-12 12:21:21 | ||
图片预览




文档简介
课件15张PPT。北师大版高中数学必修4
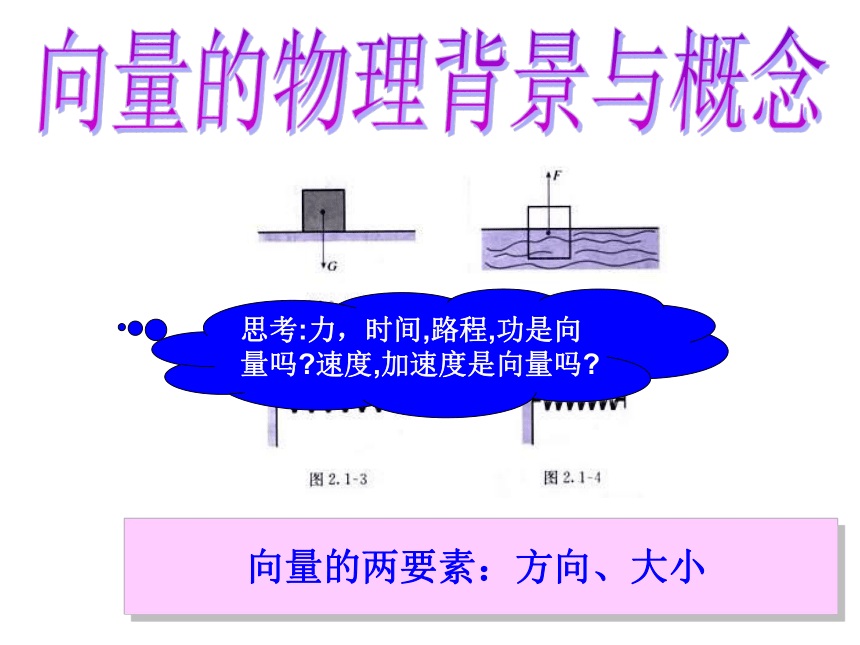
第二章《平面向量》2.1 从位移、速度、力到向量向量的物理背景与概念数量:只有大小,没有方向的量。
向量:既有大小,又有方向的量。思考:力,时间,路程,功是向量吗?速度,加速度是向量吗?
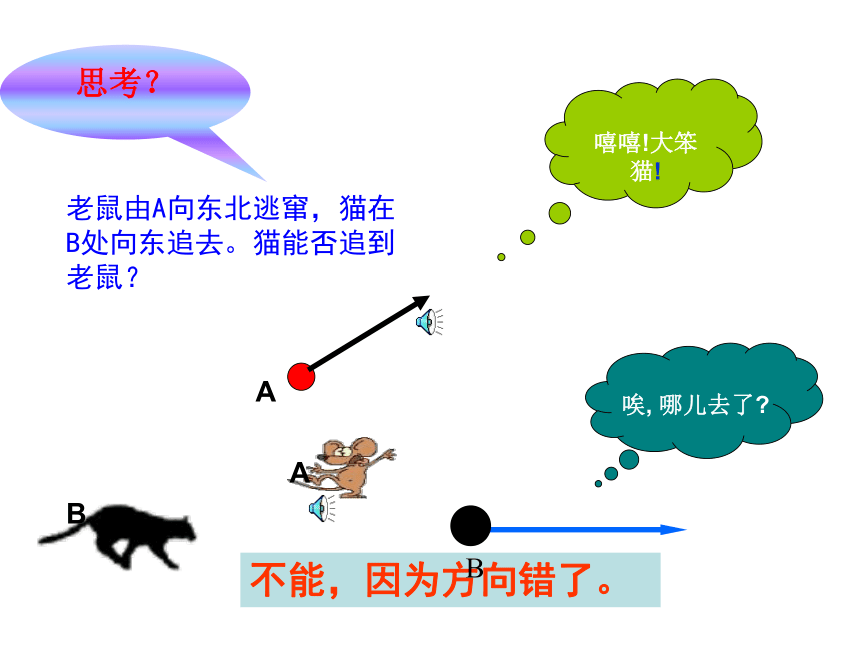
唉, 哪儿去了?
嘻嘻!大笨猫!AB老鼠由A向东北逃窜,猫在B处向东追去。猫能否追到老鼠?思考?不能,因为方向错了。 A向量的概念数量:只有大小,没有方向的量统称为数量。数量常常用数轴上的一个点表示,如3,2,-1,…而且不同的点表示不同的数量。向量:既有大小又有方向的量统称为向量。
向量两要素:大小和方向。
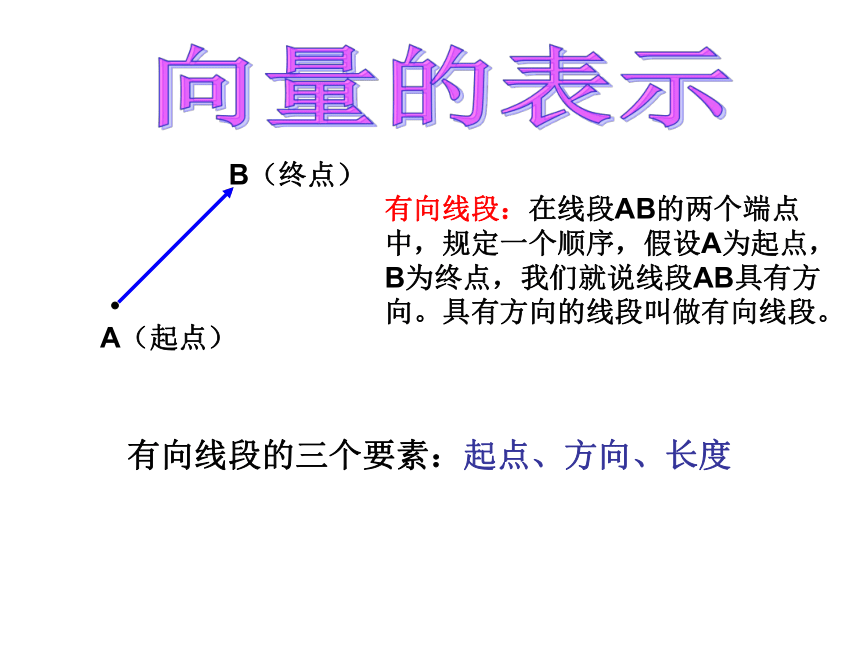
有向线段:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向。具有方向的线段叫做有向线段。有向线段的三个要素:起点、方向、长度A(起点)B(终点)向量的表示1、向量的几何表示:用有向线段表示向量的表示1.温度含零上和零下温度,所以温度是向量( ) ××2.向量的模是一个正实数。( )×注:向量不能比较大小长度相等且方向相同的两个向量表示相等向量,
但是两个向量之间只有相等关系,没有大小之分,“对于向量 , , > ,或 < ”这种说法是错误的. 平行向量又叫做共线向量各向量的终点与直线m之间有什么关系?相等向量与共线向量向量相等 向量平行平行向量一定是相等向量吗?相等向量与共线向量11个相等向量与共线向量习题探析 1.判断下列命题是否正确,若不正确,请简述理由.
?
①向量 与 是共线向量,则A、B、C、D 四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量(长度相同,方向相反的向量)不相等;
?
④共线的向量,若起点不同,则终点一定不同。(×)(×)(×)(×)2.下面几个命题: C A.0 B. 1 C. 2 D. 3 其中正确的个数是( )
习题探析3.某人从A点出发向东走了5米到达B点,然后改变方向按东北方向走了 米到达C点,到达C点后又改变方向向西走了10米到达D点(1)作出向量AB,BC,CD;(2) 求AD的模AB CD归纳小结作业:P73 习题2—1
1、2、3、4
课后反思:
第二章《平面向量》2.1 从位移、速度、力到向量向量的物理背景与概念数量:只有大小,没有方向的量。
向量:既有大小,又有方向的量。思考:力,时间,路程,功是向量吗?速度,加速度是向量吗?
唉, 哪儿去了?
嘻嘻!大笨猫!AB老鼠由A向东北逃窜,猫在B处向东追去。猫能否追到老鼠?思考?不能,因为方向错了。 A向量的概念数量:只有大小,没有方向的量统称为数量。数量常常用数轴上的一个点表示,如3,2,-1,…而且不同的点表示不同的数量。向量:既有大小又有方向的量统称为向量。
向量两要素:大小和方向。
有向线段:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,我们就说线段AB具有方向。具有方向的线段叫做有向线段。有向线段的三个要素:起点、方向、长度A(起点)B(终点)向量的表示1、向量的几何表示:用有向线段表示向量的表示1.温度含零上和零下温度,所以温度是向量( ) ××2.向量的模是一个正实数。( )×注:向量不能比较大小长度相等且方向相同的两个向量表示相等向量,
但是两个向量之间只有相等关系,没有大小之分,“对于向量 , , > ,或 < ”这种说法是错误的. 平行向量又叫做共线向量各向量的终点与直线m之间有什么关系?相等向量与共线向量向量相等 向量平行平行向量一定是相等向量吗?相等向量与共线向量11个相等向量与共线向量习题探析 1.判断下列命题是否正确,若不正确,请简述理由.
?
①向量 与 是共线向量,则A、B、C、D 四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量(长度相同,方向相反的向量)不相等;
?
④共线的向量,若起点不同,则终点一定不同。(×)(×)(×)(×)2.下面几个命题: C A.0 B. 1 C. 2 D. 3 其中正确的个数是( )
习题探析3.某人从A点出发向东走了5米到达B点,然后改变方向按东北方向走了 米到达C点,到达C点后又改变方向向西走了10米到达D点(1)作出向量AB,BC,CD;(2) 求AD的模AB CD归纳小结作业:P73 习题2—1
1、2、3、4
课后反思:
