2021—2022学年华东师大版九年级数学上册23.4中位线 课件 (共33张PPT)
文档属性
| 名称 | 2021—2022学年华东师大版九年级数学上册23.4中位线 课件 (共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 13.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 21:47:51 | ||
图片预览







文档简介
(共33张PPT)
23.4中位线
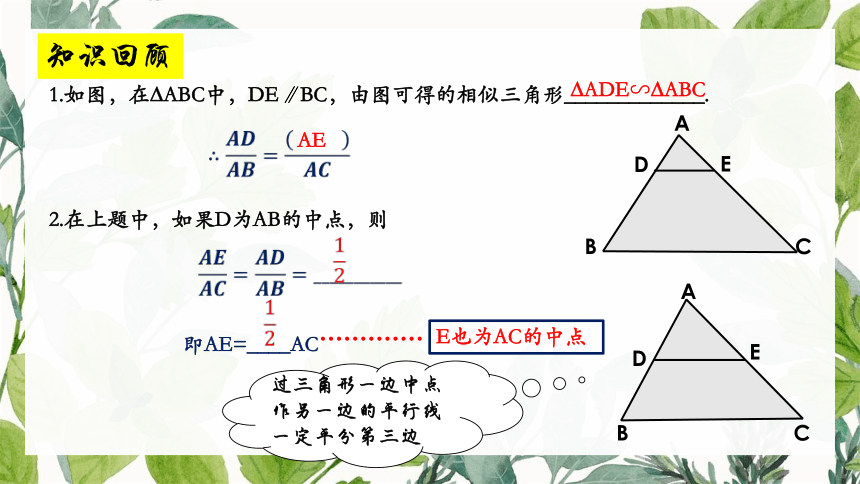
知识回顾
D
A
B
C
E
1.如图,在 ABC中,DE∥BC,由图可得的相似三角形_____________.
ADE∽ ABC
AE
2.在上题中,如果D为AB的中点,则
即AE=____AC
E也为AC的中点
E
A
B
C
D
过三角形一边中点作另一边的平行线一定平分第三边
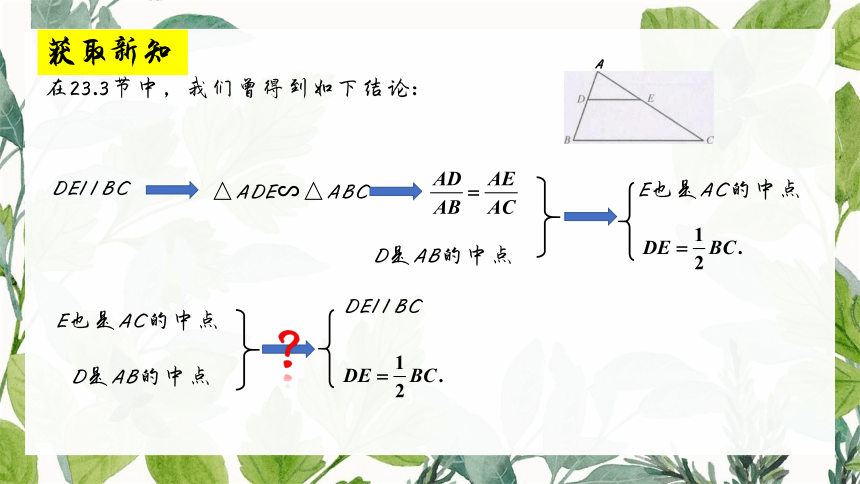
获取新知
在23.3节中,我们曾得到如下结论:
A
DE//BC
△ADE∽△ABC
D是AB的中点
E也是AC的中点
D是AB的中点
E也是AC的中点
DE//BC
猜想
C
如图,在△ABC中,点D、E分别是
AB与AC 的中点.根据画出的图形,
可以猜想:
DE // BC,且DE = BC.
对此,我们可以用演绎推理给出证明.
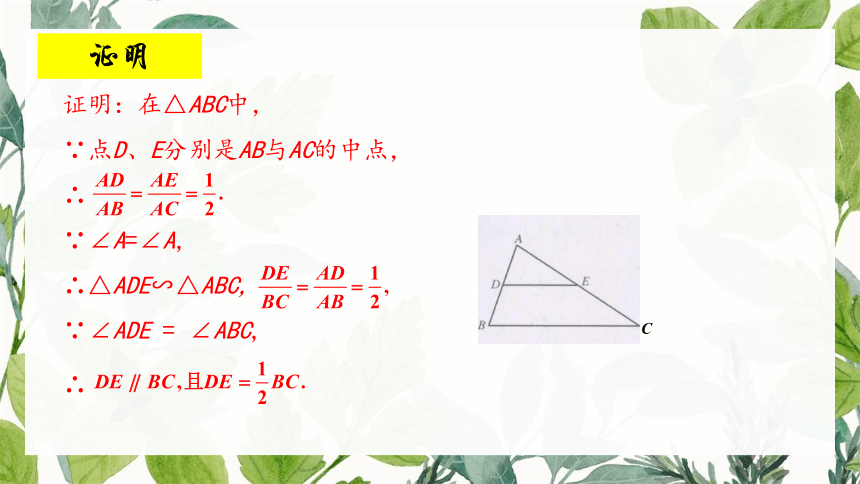
证明
证明:在△ABC中,
∵点D、E分别是AB与AC的中点,
∴
∵∠A=∠A,
∴△ADE∽△ABC,
∵∠ADE = ∠ABC,
∴
C
知识点总结
知识点
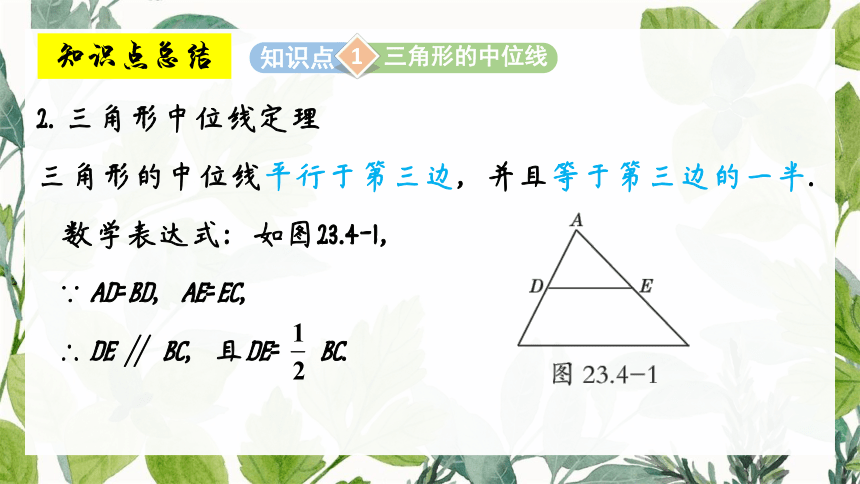
三角形的中位线
1
1. 三角形的中位线的定义
连结三角形两边中点的线段叫做三角形的中位线.
数学表达式:如图23.4-1,∵ AD=BD,AE=EC,
∴ DE 是△ ABC 的中位线.
知识点总结
知识点
三角形的中位线
1
特别提醒:
1. 一个三角形有三条中位线;
2. 三条中位线将原三角形分割成四个全等的三角形,三个面积相等的平行四边形;
3. 三角形的中位线与三角形的中线的区别:三角形的中线是连结一顶点和它的对边中点的线段,而三角形的中位线则是连结两边中点的线段;
4. 三角形的一条中位线与第三边上的中线互相平分.
知识点总结
知识点
三角形的中位线
1
2. 三角形中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半.
数学表达式:如图23.4-1,
∵ AD=BD,AE=EC,
∴ DE ∥ BC,且DE= BC.
知识点总结
知识点
三角形的中位线
1
3. 三角形的中位线的应用
(1)三角形的中位线定理反映了三角形的中位线与第三边的双重关系:一是位置关系,可以用来证两直线平行;二是数量关系,可以用来证线段的倍分关系.
知识点总结
知识点
三角形的中位线
1
(2)中位线具有平移角、倍分转化线段的功能,因此当遇到中点或中线时,应考虑构造中位线,即我们常说的“遇到中点想中位线”;相应地,若知道了三角形的中位线,则三角形两边的中点即可找到.
知识应用——例题解析
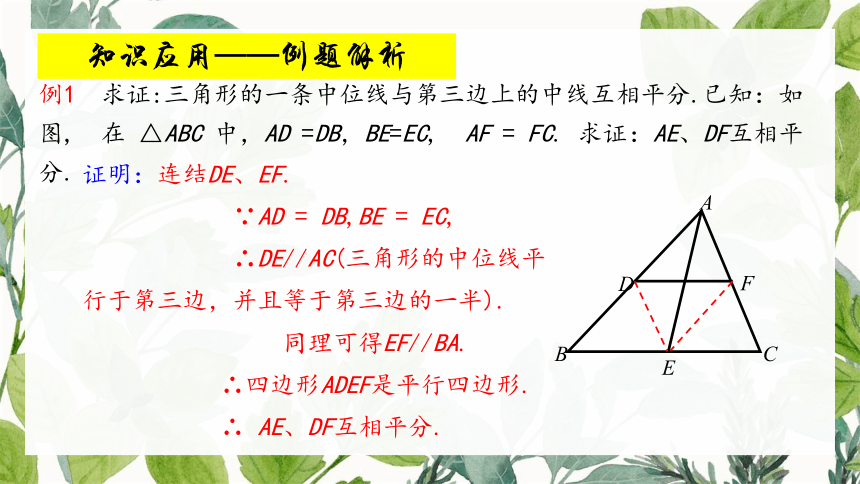
例1 求证:三角形的一条中位线与第三边上的中线互相平分.已知:如图, 在 △ABC 中,AD =DB,BE=EC, AF = FC. 求证:AE、DF互相平分.
证明:连结DE、EF.
∵AD = DB,BE = EC,
∴DE//AC(三角形的中位线平行于第三边,并且等于第三边的一半).
同理可得EF//BA.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分.
D
A
B
C
F
E
知识应用——例题解析
例2 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于点G. 求证:
证明:连结ED.
∵D、E分别是边BC、AB的中点,
∴DE//AC , (三角形的中位线平行于第
三边,并且等于第三边的一半).
∴△ACG∽△DEG,
∴
E
A
B
C
D
G
知识应用——真题演练
如图23.4-2,已知E 为平行四边形ABCD 中DC 边延长线上一点,且CE=DC,连结AE,分别交BC,BD 于点F,G,连结AC 交BD 于点O,连结OF.求证:AB=2OF.
1
知识应用——真题演练
证明:如图23.4-2,连结BE.
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD.
∵E为平行四边形ABCD中DC边延长线上一点,
且CE=DC,
∴AB∥CE,AB=CE,∴四边形ABEC是平行四边形,
∴点F是BC的中点.
又∵点O是AC的中点,∴OF是△ABC的中位线,∴AB=2OF.
知识应用——真题演练
如图,M 是△ ABC的边BC 的中点,AN 平分∠ BAC,BN ⊥ AN 于点N, 延长BN 交AC 于点D, 连结MN. 已知AB=10,BC=15,MN=3.
(1)求证:BN=DN;
(2)求△ ABC 的周长.
2
知识应用——真题演练
(1)证明:∵AN平分∠BAD,
∴∠1=∠2.
∵BN⊥AN,∴∠ANB=∠AND=90°.
又∵AN=AN,∴△ABN≌△ADN(ASA).
∴BN=DN.
(2)解:∵△ABN≌△ADN,
∴AD=AB=10.
∵DN=BN,点M是BC的中点,
∴MN是△BDC的中位线.
∴CD=2MN=6.
∴△ABC的周长为AB+BC+CD+AD=10+15+6+10=41.
获取新知
B
C
D
F
G`
A
G`
三角形的重心的定义:三角形的重心是三角形三
条中线的交点.
三角形重心的性质:三角形的重心与一边中点的
连线的长是对应中线长的
如果在上图中,取AC的中点F,假设BF与AD交于G',如下图,那么我们同理有, 所以有 ,即两图中的点G与G'是重合的.
于是我们有以下结论:
知识点总结
知识点
三角形的重心
2
1. 三角形的重心:
三角形三条边上的中线交于一点,这个点就是三角形的重心.
特别提醒:
●三角形的重心到顶点的距离等于它到对边中点距离的2 倍.
●三角形的重心是三角形中每条中线的一个三等分点.
知识点总结
知识点
三角形的重心
2
2. 三角形重心的性质定理:
三角形的重心与一边中点的连线的长是对应中线长的
注意:连结三角形顶点和重心的直线必然平分这个顶点的对边.
综合应用
1.如图是一块等腰三角形空地ABC,已知D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米.若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是( )
A.22米 B.17米 C.14米 D.11米
B
综合应用
2.如图所示,已知点E、F分别是△ABC的边AC、AB的中点,BE、CF相交于点G,FG=1,则CF的长为( )
A.2 B.1.5 C.3 D.4
C
3.如图所示,在△ABC中,G为重心,连结AG并延长,交边BC于点D,若△ABC的面积为6 cm2,则△BGD的面积为_______.
1cm2
综合应用
4.在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,
则EF和MN的关系是_______________.
平行且相等
达标训练
C
达标训练
B
达标训练
100
达标训练
8
达标训练
5.如图,点G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,且EF+BC=7.2 cm,求BC的长.
达标训练
达标训练
拓展研究(A1必做,A2选做)
课程总结——思维导图
中位线
三角形的中位线
两边的
中点
分中线长为1∶2
重心
平行于第三边
等于第三边的一半
关键
拓展
数量关系
数量关系
位置关系
你学会了吗?
23.4中位线
知识回顾
D
A
B
C
E
1.如图,在 ABC中,DE∥BC,由图可得的相似三角形_____________.
ADE∽ ABC
AE
2.在上题中,如果D为AB的中点,则
即AE=____AC
E也为AC的中点
E
A
B
C
D
过三角形一边中点作另一边的平行线一定平分第三边
获取新知
在23.3节中,我们曾得到如下结论:
A
DE//BC
△ADE∽△ABC
D是AB的中点
E也是AC的中点
D是AB的中点
E也是AC的中点
DE//BC
猜想
C
如图,在△ABC中,点D、E分别是
AB与AC 的中点.根据画出的图形,
可以猜想:
DE // BC,且DE = BC.
对此,我们可以用演绎推理给出证明.
证明
证明:在△ABC中,
∵点D、E分别是AB与AC的中点,
∴
∵∠A=∠A,
∴△ADE∽△ABC,
∵∠ADE = ∠ABC,
∴
C
知识点总结
知识点
三角形的中位线
1
1. 三角形的中位线的定义
连结三角形两边中点的线段叫做三角形的中位线.
数学表达式:如图23.4-1,∵ AD=BD,AE=EC,
∴ DE 是△ ABC 的中位线.
知识点总结
知识点
三角形的中位线
1
特别提醒:
1. 一个三角形有三条中位线;
2. 三条中位线将原三角形分割成四个全等的三角形,三个面积相等的平行四边形;
3. 三角形的中位线与三角形的中线的区别:三角形的中线是连结一顶点和它的对边中点的线段,而三角形的中位线则是连结两边中点的线段;
4. 三角形的一条中位线与第三边上的中线互相平分.
知识点总结
知识点
三角形的中位线
1
2. 三角形中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半.
数学表达式:如图23.4-1,
∵ AD=BD,AE=EC,
∴ DE ∥ BC,且DE= BC.
知识点总结
知识点
三角形的中位线
1
3. 三角形的中位线的应用
(1)三角形的中位线定理反映了三角形的中位线与第三边的双重关系:一是位置关系,可以用来证两直线平行;二是数量关系,可以用来证线段的倍分关系.
知识点总结
知识点
三角形的中位线
1
(2)中位线具有平移角、倍分转化线段的功能,因此当遇到中点或中线时,应考虑构造中位线,即我们常说的“遇到中点想中位线”;相应地,若知道了三角形的中位线,则三角形两边的中点即可找到.
知识应用——例题解析
例1 求证:三角形的一条中位线与第三边上的中线互相平分.已知:如图, 在 △ABC 中,AD =DB,BE=EC, AF = FC. 求证:AE、DF互相平分.
证明:连结DE、EF.
∵AD = DB,BE = EC,
∴DE//AC(三角形的中位线平行于第三边,并且等于第三边的一半).
同理可得EF//BA.
∴四边形ADEF是平行四边形.
∴ AE、DF互相平分.
D
A
B
C
F
E
知识应用——例题解析
例2 如图,在△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于点G. 求证:
证明:连结ED.
∵D、E分别是边BC、AB的中点,
∴DE//AC , (三角形的中位线平行于第
三边,并且等于第三边的一半).
∴△ACG∽△DEG,
∴
E
A
B
C
D
G
知识应用——真题演练
如图23.4-2,已知E 为平行四边形ABCD 中DC 边延长线上一点,且CE=DC,连结AE,分别交BC,BD 于点F,G,连结AC 交BD 于点O,连结OF.求证:AB=2OF.
1
知识应用——真题演练
证明:如图23.4-2,连结BE.
∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD.
∵E为平行四边形ABCD中DC边延长线上一点,
且CE=DC,
∴AB∥CE,AB=CE,∴四边形ABEC是平行四边形,
∴点F是BC的中点.
又∵点O是AC的中点,∴OF是△ABC的中位线,∴AB=2OF.
知识应用——真题演练
如图,M 是△ ABC的边BC 的中点,AN 平分∠ BAC,BN ⊥ AN 于点N, 延长BN 交AC 于点D, 连结MN. 已知AB=10,BC=15,MN=3.
(1)求证:BN=DN;
(2)求△ ABC 的周长.
2
知识应用——真题演练
(1)证明:∵AN平分∠BAD,
∴∠1=∠2.
∵BN⊥AN,∴∠ANB=∠AND=90°.
又∵AN=AN,∴△ABN≌△ADN(ASA).
∴BN=DN.
(2)解:∵△ABN≌△ADN,
∴AD=AB=10.
∵DN=BN,点M是BC的中点,
∴MN是△BDC的中位线.
∴CD=2MN=6.
∴△ABC的周长为AB+BC+CD+AD=10+15+6+10=41.
获取新知
B
C
D
F
G`
A
G`
三角形的重心的定义:三角形的重心是三角形三
条中线的交点.
三角形重心的性质:三角形的重心与一边中点的
连线的长是对应中线长的
如果在上图中,取AC的中点F,假设BF与AD交于G',如下图,那么我们同理有, 所以有 ,即两图中的点G与G'是重合的.
于是我们有以下结论:
知识点总结
知识点
三角形的重心
2
1. 三角形的重心:
三角形三条边上的中线交于一点,这个点就是三角形的重心.
特别提醒:
●三角形的重心到顶点的距离等于它到对边中点距离的2 倍.
●三角形的重心是三角形中每条中线的一个三等分点.
知识点总结
知识点
三角形的重心
2
2. 三角形重心的性质定理:
三角形的重心与一边中点的连线的长是对应中线长的
注意:连结三角形顶点和重心的直线必然平分这个顶点的对边.
综合应用
1.如图是一块等腰三角形空地ABC,已知D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米.若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是( )
A.22米 B.17米 C.14米 D.11米
B
综合应用
2.如图所示,已知点E、F分别是△ABC的边AC、AB的中点,BE、CF相交于点G,FG=1,则CF的长为( )
A.2 B.1.5 C.3 D.4
C
3.如图所示,在△ABC中,G为重心,连结AG并延长,交边BC于点D,若△ABC的面积为6 cm2,则△BGD的面积为_______.
1cm2
综合应用
4.在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,
则EF和MN的关系是_______________.
平行且相等
达标训练
C
达标训练
B
达标训练
100
达标训练
8
达标训练
5.如图,点G是△ABC的重心,过点G作EF∥BC,分别交AB、AC于点E、F,且EF+BC=7.2 cm,求BC的长.
达标训练
达标训练
拓展研究(A1必做,A2选做)
课程总结——思维导图
中位线
三角形的中位线
两边的
中点
分中线长为1∶2
重心
平行于第三边
等于第三边的一半
关键
拓展
数量关系
数量关系
位置关系
你学会了吗?
