平方差公式

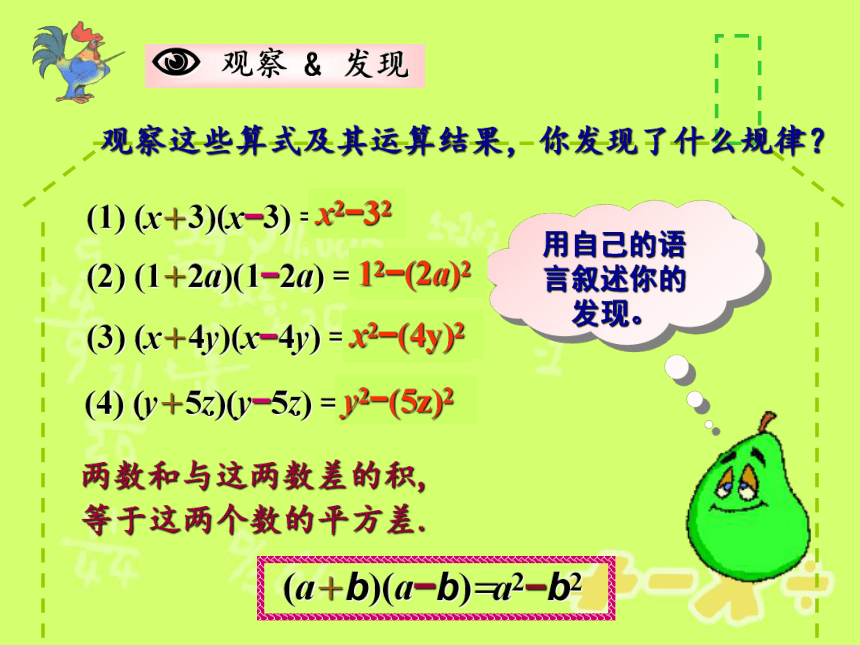
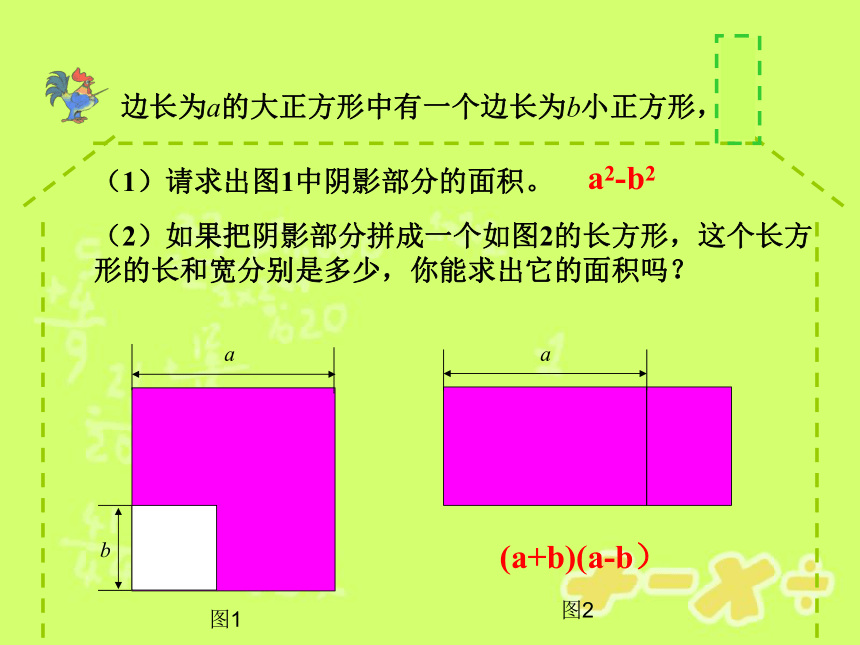
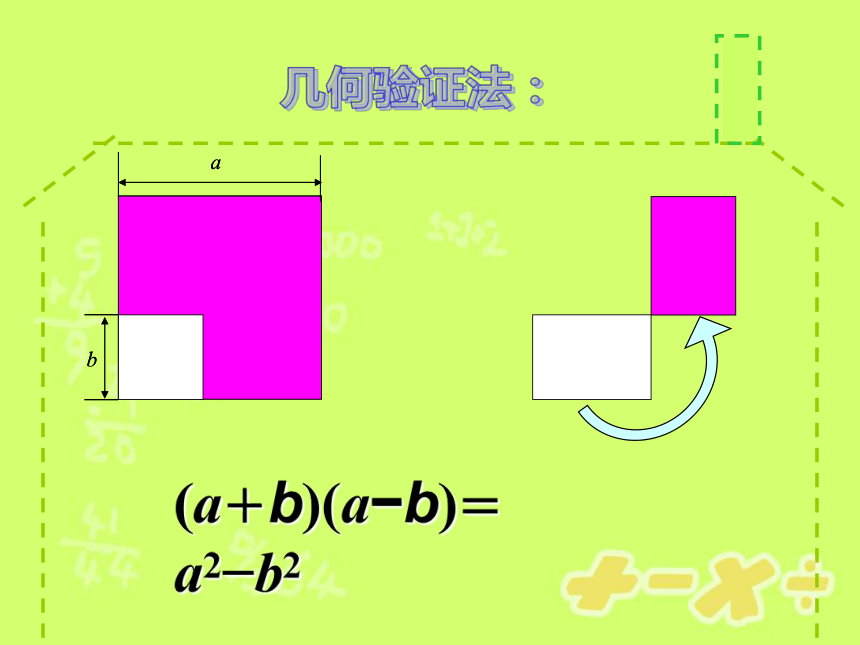
课件15张PPT。 (a+b)(m+n)=am+an+bm+bn用多项式的乘法法则计算：做一做x2?91?4a2x2?16y2y2?25z2观察这些算式及其运算结果，你发现了什么规律？两数和与这两数差的积,等于这两个数的平方差.(a+b)(a?b)=a2?b2x2?3212?(2a)2x2?(4y)2y2?(5z)2平方差公式验证：(a+b)(a?b)= a2?b2代数验证法：（多项式的乘法法则）（合并同类项）图1图2边长为a的大正方形中有一个边长为b小正方形，（1）请求出图1中阴影部分的面积。（2）如果把阴影部分拼成一个如图2的长方形，这个长方形的长和宽分别是多少，你能求出它的面积吗？a2-b2(a+b)(a-b）(a+b)(a?b)= a2?b2几何验证法： 注意：必须符合平方差公式特征的代数式才能用平方差公式.判断下列式子可以用平方差公式计算吗？为什么？(1) (?a+b)(?a?b) ；
(2) (a?b)(b?a) ;
(3) (a+2b)(2b?c);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (能) (不能) (不能) (能) (不能) 例1 ：运用平方差公式计算：
(1) (2x+1)(2x ?1)； (2) (x+2y)(x?2y).=4x2-1(2) 解： (x+2y)(x-2y)=(1) 解：(2x+1)(2x-1)=(2x)2-12x2-(2y)2=x2-4y2(2) (4a+b)(?b+4a)例2 ：运用平方差公式计算：解：原式＝(4a)2? b2＝16a2? b2 1002×998= 10002-22= 1000000 – 4 = 999996例3 ：运用平方差公式做简便计算：1. （ ）·（ ） =n2-m2
2. （ ）·（ ） =4x2-9y2

3. （ 5+a ）·（ ） =25-a2逆向思维训练：n+mn-m2x+3y2x-3y5-a两数和与这两数差的积，等于它们的平方差。本节课你学到了什么?用语言表述：谢谢指导！