人教版五年级下学期数学总复习课件(共34张PPT)
文档属性
| 名称 | 人教版五年级下学期数学总复习课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 436.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 19:28:22 | ||
图片预览










文档简介
(共34张PPT)
人教版五年级下册
知识小结 整理与复习
图形的运动
长方体和正方体
课程
结构
*观察物体
折线统计图
分数
因数与倍数
back
找次品品
因数和倍数
1. 因数和倍数
2. 2 ,3 , 5 倍数的特点
拓展4,8, 9倍数的特点
3. 公因数与公倍数
4. 奇数与偶数 质数与合数
因数和倍数
在整数乘法里,如果a×b=c,
那么a和b是c的因数,c是a和b的倍数。
一个数的最大因数与最小倍数都是( )
练习:
1. 3×8=24中,3和8都是24的( )。24是3和8的( )
2.判断:
根据算式25×2=50,我们可以说2和25是因数,50是倍数。 ( )
因为2.5×4=10,所以说10是2.5的倍数。 ( )
3.m是n的5倍,那么m和n的最小公倍数是( );最大公因数是( )
4.一个数的因数有1,2,3,4,6,12这个数是( )
back
因数和倍数
它本身
因数
倍数
×
×
m=5×n
2、3、5倍数的特点
2的倍数——个位上是0、2、4、6、8的数
5的倍数——个位上是0、5的数
既是2的倍数,也是5的倍数——个位上是0数
3的倍数——各数位上的数字之和是3的倍数
练习:
1,一个数是25△,△里最小填( ),能被3整除,最小填( )能被2整除,最小填( )能被5整除。
2,判断:如果一个数是6的倍数,那么它也是2和3的倍数。 ( )
(2+5+?)÷3
4、8、9倍数的特点
最后两位数如果是4的倍数,这个数就是4的倍数
最后三位如果是8的倍数,这个数就是8的倍数
各个数位上数字和是9的倍数,这个数就是9的倍数
728、642、578、9603、5455、5120
拓展练习
小朋友到文具店买日记本,日记本的单价已看不清楚,他买了3本日记本,售货员阿姨说应付134元,小红认为不对。你能解释这是为什么吗?
1+3+4=8 8不是3的倍数,而买三本,所以总价一定能被3整除,134不是3的倍数,所以不对。
一个长方形的长和宽都是自然数,面积是36平方米,这样的形状不同的长方形共有多少种?
1×36=36 2×18=36 3×12=36 4×9=36
6×6=36(正方形,特殊的 长方形)
back
公因数与公倍数
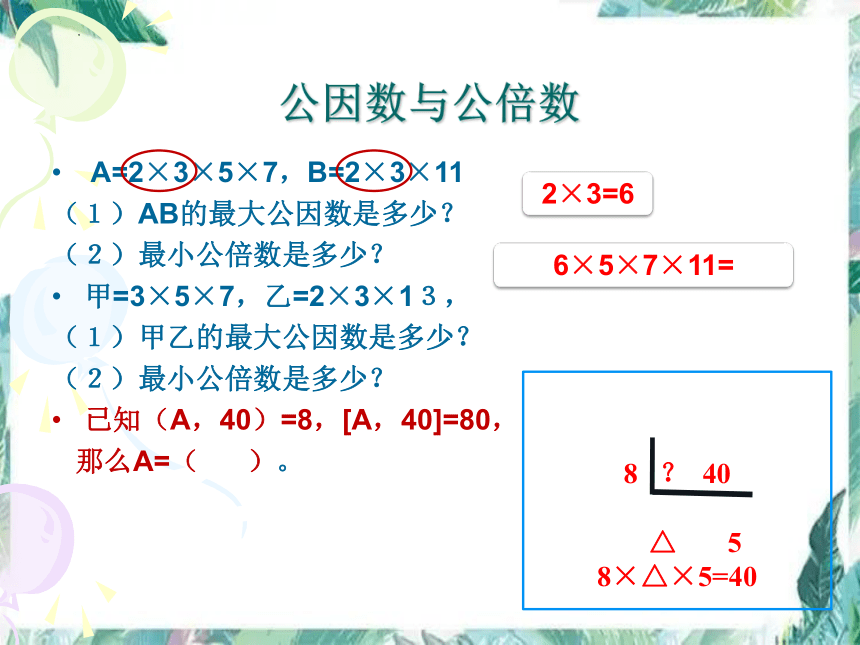
A=2×3×5×7,B=2×3×11
(1)AB的最大公因数是多少?
(2)最小公倍数是多少?
甲=3×5×7,乙=2×3×13,
(1)甲乙的最大公因数是多少?
(2)最小公倍数是多少?
已知(A,40)=8,[A,40]=80,
那么A=( )。
2×3=6
6×5×7×11=
8 ? 40
△ 5
8×△×5=40
一筐苹果4个4个拿,6个6个拿,或者8个8个拿都正好拿完,这筐苹果最少有多少个?
【4,6,8】=24
答:这筐苹果最少有24个
有200多个学生,他们每6人站一队正好,每7人一行也正好不多不少,有多少学生?
【 6,7】=42 200÷42≈5 42×5=210(人)
答 :有210个学生。
把长120厘米,宽80厘米的铁板裁成面积相等,最大的正方形而且没有剩余,可以裁成多少块?
(120,80)=40 120×80÷(40×40)=6(个)
120÷40=3 (个) 80÷40=2 (个) 3 ×2=6(个)
back
奇数与偶数
自然数中,
是2的倍数的数叫做偶数(0也是偶数),
不是2的倍数的数叫做奇数
最小的奇数是( ),最小的偶数是( )
奇偶性:
偶数+偶数= 奇数+奇数= 偶数+奇数=
1、质数与合数数
只有1和它本身两个因数的数叫做质数/素数
除了1和它本身还有别的因数的数叫做合数。
1既不是质数,也不是合数。
最小的质数是( ),最小的合数是( )。。
自然数按(因数的个数多少),分为1、质数、合数;
按(是否是2的倍数),可以分为奇数、偶数。
拓展提高
1.两个不同的质数相乘的结果是( ),它有( )个因数。
2.下面的式子,( )是分解质因数。
①54=2×3×9 ②42=2×3×7 ③15=3×5×1
3.一个数个位是最小的质数,十位是最小合数的2倍,百位是最小的偶数,千位是最小的奇数,万位上的数的最小倍数是9,这个数是( )
91082
a,b两个质数的积是ab,因数有1,a,b,ab
√
长方体与正方体
长方体与正方体的认识
表面积与体积
容积
单位
正方体 长方体
棱长和 棱长×12 (长+宽+高)×4
表面积 棱长×棱长×6 (长×宽+长×高+宽×高)×2
体 积 棱长×棱长×棱长 长×宽×高
长方体的侧面积=底面周长×高
练习
1.一个棱长为12厘米的正方体,它的棱长总和是( )厘米。
2.有一根长60厘米的铁丝,将它围成一个正方体的框架,围成的正方体的棱长是( )厘米。
3.一个长为12厘米,宽为8厘米,高为4厘米的长方体,它的棱长总和是( )厘米。
4.有一根长72厘米的铁丝,可以将它围成一个长3厘米,宽2厘米,高( )厘米的长方体。
用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?
棱长和不变:
8×12=96cm
96÷4=24cm 24-10-7=7cm
60÷12=5cm
长宽高之和72÷4=18cm
高:18-3-2=
有两个同样大小的正方体,他们的棱长都是5米,现在将两个正方体叠放在一块,它的表面积是多少平方米?
要做一个棱长是45厘米的无盖鱼缸,至少需要多少平方厘米的玻璃
一个正方体的表面积是384平方厘米,它的棱长是多少?
做一个无盖的铁箱,长1米,宽5分米,高8分米,至少需要多少平方米的铁皮?
求棱长6分米的正方体的表面积和体积.
判断(如果不对请说明棱长6分米的正方体的表面积和体积相等
如图:高6米,上面40平方米,右侧面积30平方米,求长方体的表面积。
宽: 30÷6=5(米) 长:40÷5=8(米)
前面面积:
6×8=48(平方米)
表面积:(40+30+48)×2
体积与面积
一个正方体的棱长是1米,
(1)他的表面积和体积分别是多少?
(2)现将它的棱长扩大2倍,他的表面积和体积分别是多少?
1个长方体或正方体,如果所有的棱长都扩大n倍,那么棱长总和也扩大n倍,表面积扩大 倍,体积扩大 倍。
一个正方体的棱长缩小3倍,他的表面积缩小( )倍,他的体积缩小( )倍
表面积:1×1×6=6平方米 体积1×1×1=1立方米
表面积:(1×2)×(1×2)×6=1×1×6×2×2=6×4=24平方米
体积(1×2)×(1×2)×(1×2)=1×1×1×2×2×2=8立方米
表面积变大
多出了黄色的正方体前后左右4个面
被覆盖
补覆盖面
每切一刀多2个面
3-1=2 增加的面的个数2×2=4(个)
所增的每个面的面积80÷4=20平方厘米
体积=底面积×高=20×15=300立方厘米
1立方分米=1升=1000毫升
练习:一个长宽高分别是8米,5米,4米的
长方体水池,它的容积是多少多少升
常用的容积单位:升和毫升
容积是容器所能容纳物体的体积
容积
分数的意义
的意义:
表示把单位“1”平均分成7份,取其中的3份。
的分数单位是( ),再加( )个这样的分数单位就是
最小的质数。
米
按分数的意义,表示:把1米平均分成____份,取其中的_____份。
按分数与除法的关系,表示:把7米平均分成____份,取其中的1份。
一根绳子分成两段,一段长 米,一段占全长的 ,哪段长?
分数与除法及分数的性质
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
题目见资料43
真分数、假分数与带分数
真分数<1,分子<分母
假分数≥1,分子≥分母
带分数>1,带分数包括整数部分和分数部分,分数部分应当是真分数
假分数化带分数 带分数化成假分数
练习:写出只相隔一个分数单位的真分数、假分数,带分数各一个
分母是9的所有最简真分数之和
通分与约分及比较大小
将上述四个分数按照从小到大的顺序排列
分数小数互化
分数加减
简便运算
分数应用题
1.五(1)班有男生23人,女生23人,男生占全班人数的几分之几?
2.17分钟走完一段路,平均每分钟走这段路的几分之几?4分钟走几分之几?15分钟呢?
3.100千克油菜籽能榨出25千克油,平均每千克油菜籽榨多少千克油?平均每千克油需要多少菜籽?
4、加工一批零件,小明独做需要8小时完成,小李独做需要10小时完成,现在小明工作了3小时,然后小李工作了5小时,他们一起完成了这批零件的几分之几?
5. 把5克盐放入355克水中, 盐的重量占盐水的几分之几?
6.
用天平找次品规律
1、把所有物品尽可能平均地分成3份,(如余1则放入到最后一份中;如余2则分别放入到前两份中),保证找出次品而且称的次数一定最少。
2、数目与测试的次数的关系:
2~3个物体,保证能找出次品需要测的次数是1次 4~9个物体(2次)
10~27个物体(3次) 28~81个物体(4次)
82~243个物体(5次)
244~729个物体(6次)
练习找次品
有10大小形状相同的球,其中有一个是比其他的球轻,其余9个一样重,最少要称几次才能保证找出那个最轻的球?
观察物体
上面看
正面看
侧面看
图形的运动
平移
旋转
对称
折线统计图
特点:
1.能看出数据的多少
2.能清楚的看出数量的增减变化
The end!
THANKS
人教版五年级下册
知识小结 整理与复习
图形的运动
长方体和正方体
课程
结构
*观察物体
折线统计图
分数
因数与倍数
back
找次品品
因数和倍数
1. 因数和倍数
2. 2 ,3 , 5 倍数的特点
拓展4,8, 9倍数的特点
3. 公因数与公倍数
4. 奇数与偶数 质数与合数
因数和倍数
在整数乘法里,如果a×b=c,
那么a和b是c的因数,c是a和b的倍数。
一个数的最大因数与最小倍数都是( )
练习:
1. 3×8=24中,3和8都是24的( )。24是3和8的( )
2.判断:
根据算式25×2=50,我们可以说2和25是因数,50是倍数。 ( )
因为2.5×4=10,所以说10是2.5的倍数。 ( )
3.m是n的5倍,那么m和n的最小公倍数是( );最大公因数是( )
4.一个数的因数有1,2,3,4,6,12这个数是( )
back
因数和倍数
它本身
因数
倍数
×
×
m=5×n
2、3、5倍数的特点
2的倍数——个位上是0、2、4、6、8的数
5的倍数——个位上是0、5的数
既是2的倍数,也是5的倍数——个位上是0数
3的倍数——各数位上的数字之和是3的倍数
练习:
1,一个数是25△,△里最小填( ),能被3整除,最小填( )能被2整除,最小填( )能被5整除。
2,判断:如果一个数是6的倍数,那么它也是2和3的倍数。 ( )
(2+5+?)÷3
4、8、9倍数的特点
最后两位数如果是4的倍数,这个数就是4的倍数
最后三位如果是8的倍数,这个数就是8的倍数
各个数位上数字和是9的倍数,这个数就是9的倍数
728、642、578、9603、5455、5120
拓展练习
小朋友到文具店买日记本,日记本的单价已看不清楚,他买了3本日记本,售货员阿姨说应付134元,小红认为不对。你能解释这是为什么吗?
1+3+4=8 8不是3的倍数,而买三本,所以总价一定能被3整除,134不是3的倍数,所以不对。
一个长方形的长和宽都是自然数,面积是36平方米,这样的形状不同的长方形共有多少种?
1×36=36 2×18=36 3×12=36 4×9=36
6×6=36(正方形,特殊的 长方形)
back
公因数与公倍数
A=2×3×5×7,B=2×3×11
(1)AB的最大公因数是多少?
(2)最小公倍数是多少?
甲=3×5×7,乙=2×3×13,
(1)甲乙的最大公因数是多少?
(2)最小公倍数是多少?
已知(A,40)=8,[A,40]=80,
那么A=( )。
2×3=6
6×5×7×11=
8 ? 40
△ 5
8×△×5=40
一筐苹果4个4个拿,6个6个拿,或者8个8个拿都正好拿完,这筐苹果最少有多少个?
【4,6,8】=24
答:这筐苹果最少有24个
有200多个学生,他们每6人站一队正好,每7人一行也正好不多不少,有多少学生?
【 6,7】=42 200÷42≈5 42×5=210(人)
答 :有210个学生。
把长120厘米,宽80厘米的铁板裁成面积相等,最大的正方形而且没有剩余,可以裁成多少块?
(120,80)=40 120×80÷(40×40)=6(个)
120÷40=3 (个) 80÷40=2 (个) 3 ×2=6(个)
back
奇数与偶数
自然数中,
是2的倍数的数叫做偶数(0也是偶数),
不是2的倍数的数叫做奇数
最小的奇数是( ),最小的偶数是( )
奇偶性:
偶数+偶数= 奇数+奇数= 偶数+奇数=
1、质数与合数数
只有1和它本身两个因数的数叫做质数/素数
除了1和它本身还有别的因数的数叫做合数。
1既不是质数,也不是合数。
最小的质数是( ),最小的合数是( )。。
自然数按(因数的个数多少),分为1、质数、合数;
按(是否是2的倍数),可以分为奇数、偶数。
拓展提高
1.两个不同的质数相乘的结果是( ),它有( )个因数。
2.下面的式子,( )是分解质因数。
①54=2×3×9 ②42=2×3×7 ③15=3×5×1
3.一个数个位是最小的质数,十位是最小合数的2倍,百位是最小的偶数,千位是最小的奇数,万位上的数的最小倍数是9,这个数是( )
91082
a,b两个质数的积是ab,因数有1,a,b,ab
√
长方体与正方体
长方体与正方体的认识
表面积与体积
容积
单位
正方体 长方体
棱长和 棱长×12 (长+宽+高)×4
表面积 棱长×棱长×6 (长×宽+长×高+宽×高)×2
体 积 棱长×棱长×棱长 长×宽×高
长方体的侧面积=底面周长×高
练习
1.一个棱长为12厘米的正方体,它的棱长总和是( )厘米。
2.有一根长60厘米的铁丝,将它围成一个正方体的框架,围成的正方体的棱长是( )厘米。
3.一个长为12厘米,宽为8厘米,高为4厘米的长方体,它的棱长总和是( )厘米。
4.有一根长72厘米的铁丝,可以将它围成一个长3厘米,宽2厘米,高( )厘米的长方体。
用一根铁丝刚好焊成一个棱长8厘米的正方体框架,如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架,它的高应该是多少厘米?
棱长和不变:
8×12=96cm
96÷4=24cm 24-10-7=7cm
60÷12=5cm
长宽高之和72÷4=18cm
高:18-3-2=
有两个同样大小的正方体,他们的棱长都是5米,现在将两个正方体叠放在一块,它的表面积是多少平方米?
要做一个棱长是45厘米的无盖鱼缸,至少需要多少平方厘米的玻璃
一个正方体的表面积是384平方厘米,它的棱长是多少?
做一个无盖的铁箱,长1米,宽5分米,高8分米,至少需要多少平方米的铁皮?
求棱长6分米的正方体的表面积和体积.
判断(如果不对请说明棱长6分米的正方体的表面积和体积相等
如图:高6米,上面40平方米,右侧面积30平方米,求长方体的表面积。
宽: 30÷6=5(米) 长:40÷5=8(米)
前面面积:
6×8=48(平方米)
表面积:(40+30+48)×2
体积与面积
一个正方体的棱长是1米,
(1)他的表面积和体积分别是多少?
(2)现将它的棱长扩大2倍,他的表面积和体积分别是多少?
1个长方体或正方体,如果所有的棱长都扩大n倍,那么棱长总和也扩大n倍,表面积扩大 倍,体积扩大 倍。
一个正方体的棱长缩小3倍,他的表面积缩小( )倍,他的体积缩小( )倍
表面积:1×1×6=6平方米 体积1×1×1=1立方米
表面积:(1×2)×(1×2)×6=1×1×6×2×2=6×4=24平方米
体积(1×2)×(1×2)×(1×2)=1×1×1×2×2×2=8立方米
表面积变大
多出了黄色的正方体前后左右4个面
被覆盖
补覆盖面
每切一刀多2个面
3-1=2 增加的面的个数2×2=4(个)
所增的每个面的面积80÷4=20平方厘米
体积=底面积×高=20×15=300立方厘米
1立方分米=1升=1000毫升
练习:一个长宽高分别是8米,5米,4米的
长方体水池,它的容积是多少多少升
常用的容积单位:升和毫升
容积是容器所能容纳物体的体积
容积
分数的意义
的意义:
表示把单位“1”平均分成7份,取其中的3份。
的分数单位是( ),再加( )个这样的分数单位就是
最小的质数。
米
按分数的意义,表示:把1米平均分成____份,取其中的_____份。
按分数与除法的关系,表示:把7米平均分成____份,取其中的1份。
一根绳子分成两段,一段长 米,一段占全长的 ,哪段长?
分数与除法及分数的性质
分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
题目见资料43
真分数、假分数与带分数
真分数<1,分子<分母
假分数≥1,分子≥分母
带分数>1,带分数包括整数部分和分数部分,分数部分应当是真分数
假分数化带分数 带分数化成假分数
练习:写出只相隔一个分数单位的真分数、假分数,带分数各一个
分母是9的所有最简真分数之和
通分与约分及比较大小
将上述四个分数按照从小到大的顺序排列
分数小数互化
分数加减
简便运算
分数应用题
1.五(1)班有男生23人,女生23人,男生占全班人数的几分之几?
2.17分钟走完一段路,平均每分钟走这段路的几分之几?4分钟走几分之几?15分钟呢?
3.100千克油菜籽能榨出25千克油,平均每千克油菜籽榨多少千克油?平均每千克油需要多少菜籽?
4、加工一批零件,小明独做需要8小时完成,小李独做需要10小时完成,现在小明工作了3小时,然后小李工作了5小时,他们一起完成了这批零件的几分之几?
5. 把5克盐放入355克水中, 盐的重量占盐水的几分之几?
6.
用天平找次品规律
1、把所有物品尽可能平均地分成3份,(如余1则放入到最后一份中;如余2则分别放入到前两份中),保证找出次品而且称的次数一定最少。
2、数目与测试的次数的关系:
2~3个物体,保证能找出次品需要测的次数是1次 4~9个物体(2次)
10~27个物体(3次) 28~81个物体(4次)
82~243个物体(5次)
244~729个物体(6次)
练习找次品
有10大小形状相同的球,其中有一个是比其他的球轻,其余9个一样重,最少要称几次才能保证找出那个最轻的球?
观察物体
上面看
正面看
侧面看
图形的运动
平移
旋转
对称
折线统计图
特点:
1.能看出数据的多少
2.能清楚的看出数量的增减变化
The end!
THANKS
