3.3.1 从函数观点看一元二次方程 教案
文档属性
| 名称 | 3.3.1 从函数观点看一元二次方程 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 117.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 13:38:06 | ||
图片预览


文档简介
第三章 不等式
第3.3.1节 从函数观点看一元二次方程
教材首先由我们初中熟悉的一次函数、一元一次方程、一元一次不等式之间的密切联系引入。
强调了两点:一、借助函数的图形,可以解一元二次方程。二、通过求解方程可以深入理解函数的性质。
课程目标 学科素养
A. 正确理解函数零点的概念. B. 理解一元二次方程与二次函数的关系. C. 掌握图象法解一元二次方程. 1.数学抽象 函数零点概念的理解. 2.直观想象 掌握图象法解一元二次方程. 3.数学运算 函数零点的计算.
1. 会求函数的零点,并判断零点所在区间.
2. 掌握图象法解一元二次方程.
1:解下列方程:
; ②; ③.
2:填空
a>0 a<0
一次函数 的图象
一元一次方程 的根
来
源
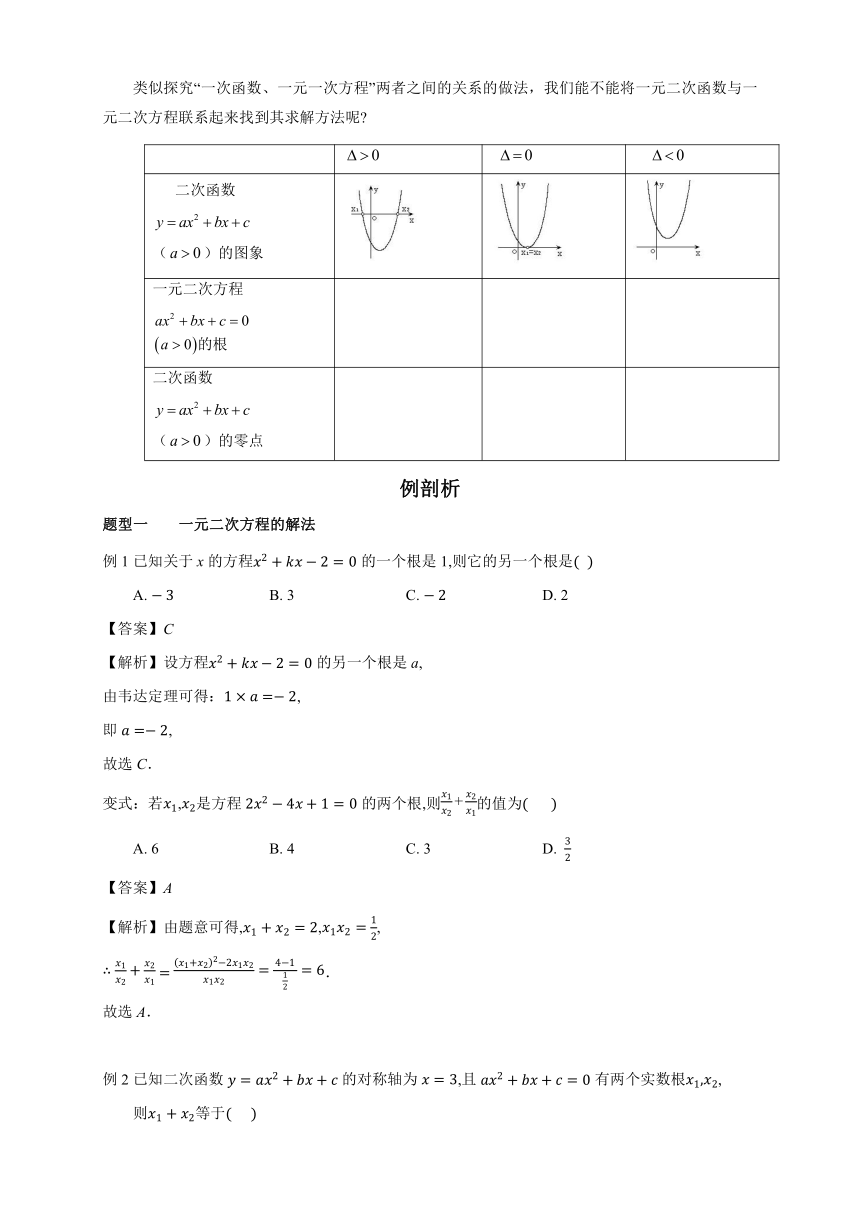
类似探究“一次函数、一元一次方程”两者之间的关系的做法,我们能不能将一元二次函数与一元二次方程联系起来找到其求解方法呢
二次函数 ()的图象
一元二次方程
二次函数 ()的零点
典例剖析
题型一 一元二次方程的解法
例1已知关于x的方程的一个根是1,则它的另一个根是
A. B. 3 C. D. 2
【答案】C
【解析】设方程的另一个根是a,
由韦达定理可得:,
即,
故选C.
变式:若,是方程的两个根,则的值为
A. 6 B. 4 C. 3 D.
【答案】A
【解析】由题意可得,,,
.
故选A.
例2已知二次函数的对称轴为,且有两个实数根,
则等于
A. 0 B. 3 C. 6 D. 不能确定
【答案】C
【解析】因为二次函数的对称轴为,
一元二次方程有两个实数根,
所以,
故选C.
变式:函数零点的个数为_____________.
【答案】2
【解析】由函数的零点与方程根的关系,
的图象与x轴的交点个数,
即为方程根的个数,
一元二次方程有两根,一元二次方程无根,
故有两根,
从而的图象与x轴的交点个数为2.
故答案为2.
题型二 由函数的零点求参数的值
例3.若二次函数y=x2+ax+b的两个零点分别是2和3,则2a+b的值为________.
解析:据题意,2+3=-a,23= b
解之得
∴2a+b=-4.
答案:-4
变式:若关于x的二次方程的两个零点分别为,,且满足,则m的值为______
【答案】
【解析】根据题意,二次方程的两个实数根分别为,,
则有,变形可得,
则,,
若,则有,
解可得:或,
又由,
则;
故答案为.
例4若二次函数的图像与x轴的交点为,,与y轴的交点为C.
若,求p的值
若的面积为105,求p的值.
【解析】由题意,令,
所以方程有两个不同的实根,
易知,为方程的两个实根,
则
,
,解得或;
即p的值为;
,,
,
,
, 解得,.
即p的值为.
题型三 由函数的零点求参数的范围
例5.已知α,β(α<β)是函数y=(x-a)(x-b)+2(aA.a<α<β【答案】 A
【解析】 设g(x)=(x-a)(x-b),
则g(x)向上平移2个单位长度得到y=(x-a)(x-b)+2的图象,
由图易知a<α<β变式:已知二次函数的两个零点为1和n,则________;
若,则a的取值范围是________.
【答案】,
【解析】二次函数的两个零点为1和n,
和n为方程的两个根,
由韦达定理得,即.
二次函数的两个零点为1和,
对称轴为, ,
二次函数,,
由,结合二次函数的图像得,
故答案为:,.
例6.一元二次方程的两根均大于2,则实数m的取值范围是
A. B. C. D.
【答案】C
【解析】设方程的两根为,
方程的两根均大于2,
则,
,即,
解得,
实数m的取值范围是.故选C.
例7.已知集合.
若A是空集,求a的取值范围;
若A中只有一个元素,求a的值,并将这个元素写出来;
若A中至多有一个元素,求a的取值范围.
【解析】若A是空集,
则方程无解
此时 即
若A中只有一个元素,
则方程有且只有一个实根,
当时方程为一元一次方程,满足条件
当,此时,解得:
或
若,则有, 若,则有;
若A中至多只有一个元素,
则A为空集,或有且只有一个元素
由,得满足条件的a的取值范围是:或
本节通过画图,看图,分析图,小组讨论列出表格深化知识,抽象概括进行教学,让每个学生动手,动口,动脑,积极参与,提高教学效率和教学质量,使学生进一步理解数形结合和从特殊到一般的思想方法。
不足之处是:有少部分学生对函数与方程之间的关系有点费解。通过了解发现:这部分同学对二次函数和方程的关系不熟悉,也就是数学基础不扎实,还有就是数形结合能力差,也就是不能建立数与形之间的联系。基于此我认为要让此类学生先从基础傲起,一点一点提高,在教学设计上要分层次,从易到难,符合学生接受知识的常规思路。这是一个循序渐进的过程。
第3.3.1节 从函数观点看一元二次方程
教材首先由我们初中熟悉的一次函数、一元一次方程、一元一次不等式之间的密切联系引入。
强调了两点:一、借助函数的图形,可以解一元二次方程。二、通过求解方程可以深入理解函数的性质。
课程目标 学科素养
A. 正确理解函数零点的概念. B. 理解一元二次方程与二次函数的关系. C. 掌握图象法解一元二次方程. 1.数学抽象 函数零点概念的理解. 2.直观想象 掌握图象法解一元二次方程. 3.数学运算 函数零点的计算.
1. 会求函数的零点,并判断零点所在区间.
2. 掌握图象法解一元二次方程.
1:解下列方程:
; ②; ③.
2:填空
a>0 a<0
一次函数 的图象
一元一次方程 的根
来
源
类似探究“一次函数、一元一次方程”两者之间的关系的做法,我们能不能将一元二次函数与一元二次方程联系起来找到其求解方法呢
二次函数 ()的图象
一元二次方程
二次函数 ()的零点
典例剖析
题型一 一元二次方程的解法
例1已知关于x的方程的一个根是1,则它的另一个根是
A. B. 3 C. D. 2
【答案】C
【解析】设方程的另一个根是a,
由韦达定理可得:,
即,
故选C.
变式:若,是方程的两个根,则的值为
A. 6 B. 4 C. 3 D.
【答案】A
【解析】由题意可得,,,
.
故选A.
例2已知二次函数的对称轴为,且有两个实数根,
则等于
A. 0 B. 3 C. 6 D. 不能确定
【答案】C
【解析】因为二次函数的对称轴为,
一元二次方程有两个实数根,
所以,
故选C.
变式:函数零点的个数为_____________.
【答案】2
【解析】由函数的零点与方程根的关系,
的图象与x轴的交点个数,
即为方程根的个数,
一元二次方程有两根,一元二次方程无根,
故有两根,
从而的图象与x轴的交点个数为2.
故答案为2.
题型二 由函数的零点求参数的值
例3.若二次函数y=x2+ax+b的两个零点分别是2和3,则2a+b的值为________.
解析:据题意,2+3=-a,23= b
解之得
∴2a+b=-4.
答案:-4
变式:若关于x的二次方程的两个零点分别为,,且满足,则m的值为______
【答案】
【解析】根据题意,二次方程的两个实数根分别为,,
则有,变形可得,
则,,
若,则有,
解可得:或,
又由,
则;
故答案为.
例4若二次函数的图像与x轴的交点为,,与y轴的交点为C.
若,求p的值
若的面积为105,求p的值.
【解析】由题意,令,
所以方程有两个不同的实根,
易知,为方程的两个实根,
则
,
,解得或;
即p的值为;
,,
,
,
, 解得,.
即p的值为.
题型三 由函数的零点求参数的范围
例5.已知α,β(α<β)是函数y=(x-a)(x-b)+2(a
【解析】 设g(x)=(x-a)(x-b),
则g(x)向上平移2个单位长度得到y=(x-a)(x-b)+2的图象,
由图易知a<α<β
若,则a的取值范围是________.
【答案】,
【解析】二次函数的两个零点为1和n,
和n为方程的两个根,
由韦达定理得,即.
二次函数的两个零点为1和,
对称轴为, ,
二次函数,,
由,结合二次函数的图像得,
故答案为:,.
例6.一元二次方程的两根均大于2,则实数m的取值范围是
A. B. C. D.
【答案】C
【解析】设方程的两根为,
方程的两根均大于2,
则,
,即,
解得,
实数m的取值范围是.故选C.
例7.已知集合.
若A是空集,求a的取值范围;
若A中只有一个元素,求a的值,并将这个元素写出来;
若A中至多有一个元素,求a的取值范围.
【解析】若A是空集,
则方程无解
此时 即
若A中只有一个元素,
则方程有且只有一个实根,
当时方程为一元一次方程,满足条件
当,此时,解得:
或
若,则有, 若,则有;
若A中至多只有一个元素,
则A为空集,或有且只有一个元素
由,得满足条件的a的取值范围是:或
本节通过画图,看图,分析图,小组讨论列出表格深化知识,抽象概括进行教学,让每个学生动手,动口,动脑,积极参与,提高教学效率和教学质量,使学生进一步理解数形结合和从特殊到一般的思想方法。
不足之处是:有少部分学生对函数与方程之间的关系有点费解。通过了解发现:这部分同学对二次函数和方程的关系不熟悉,也就是数学基础不扎实,还有就是数形结合能力差,也就是不能建立数与形之间的联系。基于此我认为要让此类学生先从基础傲起,一点一点提高,在教学设计上要分层次,从易到难,符合学生接受知识的常规思路。这是一个循序渐进的过程。
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
