北师大版数学七年级下册 2.2探索直线平行的条件学案(无答案)
文档属性
| 名称 | 北师大版数学七年级下册 2.2探索直线平行的条件学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 157.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-21 05:21:51 | ||
图片预览



文档简介
2.2.2探索直线平行的条件(2)
【学习目标】
1.经历探索平行条件的过程,掌握直线平行的条件,并能解决一些问题。
2.了解推理证明的方法。
【使用说明与学法指导】
1.先精读一遍教材P44-48页,用红笔勾画两条平行线的判定定理以及推论。针对课前预习二次阅读教材,并回答问题.
2.找出自己的疑惑和需要讨论的问题,随时记录在课本或导学案上,准备课上讨论质疑.
【课前预习】
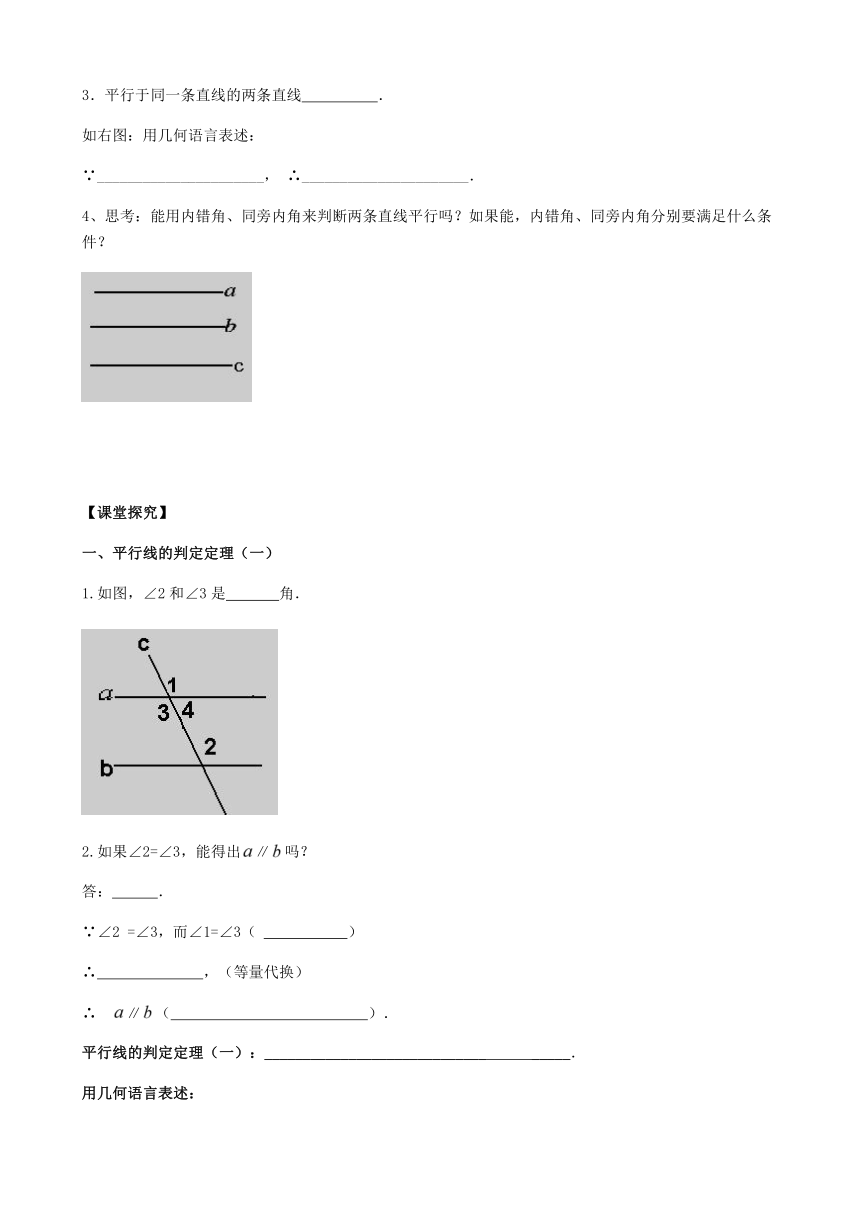
1.右图中: 是同位角,
是内错角,
是同旁内角.
2.文字简述平行理: .
如右图:用几何语言表述:
∵______________________, ∴______________________.
3.平行于同一条直线的两条直线 .
如右图:用几何语言表述:
∵______________________, ∴______________________.
4、思考:能用内错角、同旁内角来判断两条直线平行吗?如果能,内错角、同旁内角分别要满足什么条件?
【课堂探究】
一、平行线的判定定理(一)
1.如图,∠2和∠3是 角.
2.如果∠2=∠3,能得出∥吗?
答: .
∵∠2 =∠3,而∠1=∠3( )
∴ ,(等量代换)
∴ ∥( ).
平行线的判定定理(一):_____________________________ _____.
用几何语言表述:
如图(1) ∵______________________, ∴______________________.
二、平行线的判定定理(二)
已知:∠2+∠4=180°,证明:∥
证明:∵ ∠2+∠4= (已知)
+∠4=180° (邻补角定义)
∴ (同角的补角相等)
∴ ∥ ( )
平行线的判定定理(二):____________________ ________.
用几何语言表述:
如图∵_________________________, ∴_________________________.
三、推论
做一做
你能过直线AB外一点P
画直线AB的平行线吗?能画几条?
平行公理:过直线外一点有且只有 条直线与这条直线平行
(2)在下图中,分别过点C,D画直线AB的平行线EF,GH,那么EF与GH有怎样的位置关系?
平行公理推论:平行于同一条直线的两条直线 。
示例:如图:,找出互相平行的直线,并说明理由.
【学习小结】
1.判定两条直线平行的方法有哪些?
2.结合图形,用几何语言表示平行线的判定方法。
【课堂检测】
1.如图,下列结论中,不能判断AB∥CD的是( )
A.∠1=∠2 B.∠5+∠2=180° C.∠3+∠4=180° D.∠3+∠2=180°
2.如图,∠1=128°,FG平分∠EFD,则当∠2= ,AB∥CD。
3.如图,∠DAB+∠CDA=180°,∠ABC=∠1,直线AB与CD平行吗?直线AD与BC呢?为什么?
4.找出图中互相平行的线段,能说说理由吗?(点阵中相邻的四个点构成正方形)。
拓展题:已知:如图,AB⊥BC于B,CD⊥BC于C,∠1=∠2,试说明:BE∥CF.
【巩固作业】
一、基础训练
1.如图(1),AC、BC分别平分∠DAB、∠ABE,且∠1与∠2互余, 则______∥_______,理由是_________________________________________.
2.如图(2)若∠1=∠2,则______∥______,理由是____ _____;
若∠1=∠4,则______∥______,理由是__________ __________;
若∠2+∠________=180°,则c∥d,理由是______ _______________.
3.如图(3),则AB与CD的关系是 ,理由是 .
4.如图(4),请填写一个你认为恰当的条件:_______________________ ,使AD∥BC.
5. 如图,在下列四组条件中,能判定AB∥CD的是( )
∠1=∠2 B.∠3=∠4
C.∠BAD+∠ABC=180° D.∠ABD=∠BDC
6.如图,下列条件中不能判定DE∥BC的是( )
A.∠1=∠C B.∠2=∠3
C.∠1=∠2 D.∠2+∠4=180°
7.如图,已知∠1=∠2=90 ,∠3=30 ,∠4=60 ,图中有几对平行线?说说你的理由。
8.如图,已知∠1=∠2,∠3=∠4,求证:AB∥EF.
证明:∵∠1=∠2 ( )
∴ ∥ ( )
∵∠3=∠4 ( )
∴ ∥ ( )
∴AB∥EF (平行的传递性)
图(1)
图(4)
图(3)
图(2)
1
2
A
G
B
C
E
F
D
【学习目标】
1.经历探索平行条件的过程,掌握直线平行的条件,并能解决一些问题。
2.了解推理证明的方法。
【使用说明与学法指导】
1.先精读一遍教材P44-48页,用红笔勾画两条平行线的判定定理以及推论。针对课前预习二次阅读教材,并回答问题.
2.找出自己的疑惑和需要讨论的问题,随时记录在课本或导学案上,准备课上讨论质疑.
【课前预习】
1.右图中: 是同位角,
是内错角,
是同旁内角.
2.文字简述平行理: .
如右图:用几何语言表述:
∵______________________, ∴______________________.
3.平行于同一条直线的两条直线 .
如右图:用几何语言表述:
∵______________________, ∴______________________.
4、思考:能用内错角、同旁内角来判断两条直线平行吗?如果能,内错角、同旁内角分别要满足什么条件?
【课堂探究】
一、平行线的判定定理(一)
1.如图,∠2和∠3是 角.
2.如果∠2=∠3,能得出∥吗?
答: .
∵∠2 =∠3,而∠1=∠3( )
∴ ,(等量代换)
∴ ∥( ).
平行线的判定定理(一):_____________________________ _____.
用几何语言表述:
如图(1) ∵______________________, ∴______________________.
二、平行线的判定定理(二)
已知:∠2+∠4=180°,证明:∥
证明:∵ ∠2+∠4= (已知)
+∠4=180° (邻补角定义)
∴ (同角的补角相等)
∴ ∥ ( )
平行线的判定定理(二):____________________ ________.
用几何语言表述:
如图∵_________________________, ∴_________________________.
三、推论
做一做
你能过直线AB外一点P
画直线AB的平行线吗?能画几条?
平行公理:过直线外一点有且只有 条直线与这条直线平行
(2)在下图中,分别过点C,D画直线AB的平行线EF,GH,那么EF与GH有怎样的位置关系?
平行公理推论:平行于同一条直线的两条直线 。
示例:如图:,找出互相平行的直线,并说明理由.
【学习小结】
1.判定两条直线平行的方法有哪些?
2.结合图形,用几何语言表示平行线的判定方法。
【课堂检测】
1.如图,下列结论中,不能判断AB∥CD的是( )
A.∠1=∠2 B.∠5+∠2=180° C.∠3+∠4=180° D.∠3+∠2=180°
2.如图,∠1=128°,FG平分∠EFD,则当∠2= ,AB∥CD。
3.如图,∠DAB+∠CDA=180°,∠ABC=∠1,直线AB与CD平行吗?直线AD与BC呢?为什么?
4.找出图中互相平行的线段,能说说理由吗?(点阵中相邻的四个点构成正方形)。
拓展题:已知:如图,AB⊥BC于B,CD⊥BC于C,∠1=∠2,试说明:BE∥CF.
【巩固作业】
一、基础训练
1.如图(1),AC、BC分别平分∠DAB、∠ABE,且∠1与∠2互余, 则______∥_______,理由是_________________________________________.
2.如图(2)若∠1=∠2,则______∥______,理由是____ _____;
若∠1=∠4,则______∥______,理由是__________ __________;
若∠2+∠________=180°,则c∥d,理由是______ _______________.
3.如图(3),则AB与CD的关系是 ,理由是 .
4.如图(4),请填写一个你认为恰当的条件:_______________________ ,使AD∥BC.
5. 如图,在下列四组条件中,能判定AB∥CD的是( )
∠1=∠2 B.∠3=∠4
C.∠BAD+∠ABC=180° D.∠ABD=∠BDC
6.如图,下列条件中不能判定DE∥BC的是( )
A.∠1=∠C B.∠2=∠3
C.∠1=∠2 D.∠2+∠4=180°
7.如图,已知∠1=∠2=90 ,∠3=30 ,∠4=60 ,图中有几对平行线?说说你的理由。
8.如图,已知∠1=∠2,∠3=∠4,求证:AB∥EF.
证明:∵∠1=∠2 ( )
∴ ∥ ( )
∵∠3=∠4 ( )
∴ ∥ ( )
∴AB∥EF (平行的传递性)
图(1)
图(4)
图(3)
图(2)
1
2
A
G
B
C
E
F
D
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
