北师大版七年级下册 6.2 频率的稳定性课件(共27张PPT)
文档属性
| 名称 | 北师大版七年级下册 6.2 频率的稳定性课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 482.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-20 23:09:12 | ||
图片预览







文档简介
(共27张PPT)
第6章 概率初步
6.2 频率的稳定性
师生活动,概率探究
【活动1】
抛掷一枚图钉,落地后会出现两种情况:
钉尖朝上
钉尖朝下
你认为钉尖朝上和钉尖朝下的可能性一样大吗?
师生活动,概率探究
【试验操作】
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
试验总次数
钉尖朝上的次数
钉尖朝下的次数
钉尖朝上的频率(钉尖朝上的次数/试验总次数)
钉尖朝下的频率(钉尖朝下的次数/试验总次数)
在n次重复试验中,不确定事件A发生了m次,则比值m/n称为事件A发生的频率.
师生活动,概率探究
【试验操作】
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
试验总次数n
钉尖朝上的次数m
钉尖朝上的频 率m/n
师生活动,概率探究
【试验操作】
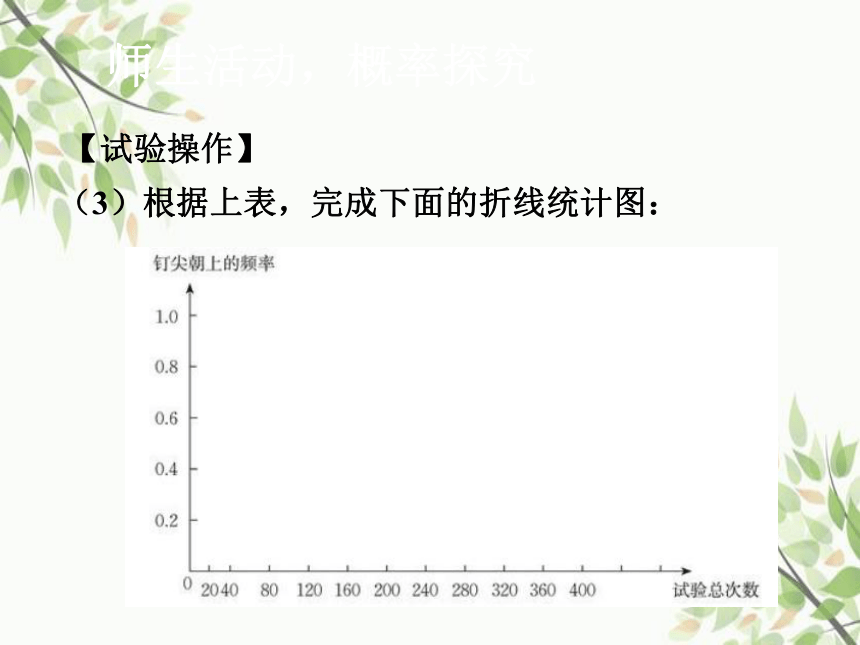
(3)根据上表,完成下面的折线统计图:
师生活动,概率探究
【试验操作】
(4)观察上面的折线统计图,钉尖朝上的频率的变化有什么规律?
在试验次数很大时,虽然我们无法保证钉尖和钉帽着地的机会均等,但钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
师生活动,概率探究
【问题讨论】
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎么想的?
由于我们无法保证钉尖和钉帽着地的机会均等,所以钉尖朝上和钉帽朝上的可能性不相等;钉尖朝上的可能性大一点.
(2)小军和小凡一起做了1 000次抛掷图钉的试验,其中有640次钉尖朝上.据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大,你同意他们的说法吗?
同意.因为做了1 000次试验,试验的次数还是比较多的.在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
师生活动,概率探究
【活动2】
抛掷一枚均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗?
师生活动,概率探究
【试验操作】
(1)同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
师生活动,概率探究
【试验操作】
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
试验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
师生活动,概率探究
【试验操作】
(3)根据上表,完成下面的折线统计图:
(4)观察上面的折线统计图,你发现了什么规律?
当抛掷硬币的次数很大时,正面朝上的频率都会在一个常数0.5附近摆动,即硬币正面朝上的频率具有稳定性.
师生活动,概率探究
【试验操作】
(5)下表列出了一些历史上的数学家所做的抛硬币试验的数据:
表中的数据支持你发现的规律吗?
支持
师生活动,概率探究
【归纳概念】
无论是抛掷质地均匀的硬币还是掷图钉,在试验次数很大时,正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
由于事件A发生的频率表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生
的可能性也越大,因而,我们就用这个常数来表示事件
A发生的可能性的大小.我们把刻画事件A发生的可能性
大小的数值,称为事件A发生的概率,记为P(A).
师生活动,概率探究
【归纳概念】
一般地,大量重复的试验中,我们常用不确定事件A发生的频率来估计事件A发生的概率.
练习:事件A发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少?
必然事件发生的概率是1;不可能事件发生的概率是0;不确定事件A发生的概率P(A)是0与1之间的一个常数.
典例剖析,解决问题
例1 有人说,既然抛掷一枚硬币出现正面的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上,你认为这种说法正
确吗?
这种说法是错误的.抛掷一枚硬币出现正面的概率为0.5,这是大量试验得出的一种规律性结果,对具体的几次试验来讲不一定能体现出这种规律性.在连续抛掷一枚硬币两次的试验中,可能两次均正面向上,也可能两次均反面向上,也可能一次正面向上,一次反面向上.
典例剖析,解决问题
例2 某种油菜籽在相同条件下的发芽试验结果表:
每批粒数n 2 5 10 70 130 310 700 1 500 2 000 3 000
发芽的粒数m 2 4 9 60 116 282 639 1 339 1 806 2 715
发芽的频率m/n 1 0.8 0.9 0.857 0.892 0.910 0.913 0.983 0.903 0.905
则估计油菜籽发芽的概率为____.
0.9
典例剖析,解决问题
例3 某厂打算生产一种中学生使用的笔袋,但无
法确定各种颜色的产量,于是该文具厂就笔袋的颜色随
机调查了5 000名中学生,并在调查到1 000名,2 000名,3 000名,4 000名,5 000名时分别计算了各种颜色的使
用频率,绘制折线图如下:
典例剖析,解决问题
(1)随着调查次数的增加,红色的频率如何变化?
随着调查次数的增加,红色的频率基本稳定在40%左右.
(2)你能估计调查到10 000名同学时,红色的频率是多少吗?
调查到10 000名同学时,红色的频率大约仍是40%.
典例剖析,解决问题
(3)如你是该厂的负责人,你将如何安排生产各种颜色笔袋的产量?
红、黄、蓝、绿以及其他颜色的生产比例大约是
4︰2︰1︰2︰1.
典例剖析,解决问题
【练习】
1.天气预报说下星期一降水概率是90%,下星期三
降水概率是10%,于是有位同学说:下星期一肯定下雨,下星期三肯定不下雨.你认为他说的对吗?
不对.所谓降水概率90%和10%是在大量的统计记录的条件下,那么它是符合大多数同等天气条件下的实际情况,但某些例外情况也是可能发生的.
典例剖析,解决问题
【练习】
2.某运动员进行射击训练,结果如下表所示:
射击次数n 20 100 200 500 800
击中靶心次数m 13 58 104 255 404
击中靶心频率m/n
(1)计算表中的频率.
0.65
0.52
0.58
0.51
0.505
(2)这个射手射击一次,击中靶心的概率是多少?
击中靶心的概率是0.5.
(3)这个射手射击1 600次,击中靶心的次数约是多少?
击中靶心的次数约是800次.
小结与作业
小结
概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况作出自己的决策.
从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,就会发现:在大量的偶然之中存在着必然的规律.
在大量重复进行同一试验时,事件A发生的频率m/n总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记为P(A).
小结与作业
小结
一些注意点:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A的概率;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0,因此0≤P(A)≤1.
小结与作业
作业
1.某射击运动员在同一条件下进行射击,结果如下:
射击总次数n 10 20 50 100 200 500 1 000
击中靶心次数m 9 16 41 88 168 429 861
击中靶心频率m/n
(1)完成上表.
(2)根据上表,画出该运动员击中靶心的频率的折线统计图.
(3)观察画出的折线统计图,击中靶心的频率的变化有什么规律?
小结与作业
作业
2.某种麦粒在相同条件下的发芽试验,结果如下:
试验的麦粒数n 100 200 500 1 000 2 000 5 000
发芽的粒数m 94 191 473 954 1 906 4 748
发芽的频率m/n
(1)完成上表;
(2)根据上表,画出麦粒发芽频率的折线统计图;
(3)任取一粒麦粒,估计它能发芽的概率.
小结与作业
作业
3.对某批乒乓球的质量进行随机抽查,结果如下:
随机抽取的乒乓球数n 10 20 50 100 200 500 1 000
优等品数m 7 16 43 81 164 414 825
优等品率m/n
(1)完成上表;
(2)根据上表,在这批乒乓球中任取一个,它为优等品的概率大约是多少?
(3)如果重新再抽取1 000个乒乓球进行质量检查,对比上表记录下数据,两表的结果会一样吗?为什么?
Happy End
第6章 概率初步
6.2 频率的稳定性
师生活动,概率探究
【活动1】
抛掷一枚图钉,落地后会出现两种情况:
钉尖朝上
钉尖朝下
你认为钉尖朝上和钉尖朝下的可能性一样大吗?
师生活动,概率探究
【试验操作】
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
试验总次数
钉尖朝上的次数
钉尖朝下的次数
钉尖朝上的频率(钉尖朝上的次数/试验总次数)
钉尖朝下的频率(钉尖朝下的次数/试验总次数)
在n次重复试验中,不确定事件A发生了m次,则比值m/n称为事件A发生的频率.
师生活动,概率探究
【试验操作】
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
试验总次数n
钉尖朝上的次数m
钉尖朝上的频 率m/n
师生活动,概率探究
【试验操作】
(3)根据上表,完成下面的折线统计图:
师生活动,概率探究
【试验操作】
(4)观察上面的折线统计图,钉尖朝上的频率的变化有什么规律?
在试验次数很大时,虽然我们无法保证钉尖和钉帽着地的机会均等,但钉尖朝上的频率,都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
师生活动,概率探究
【问题讨论】
(1)通过上面的试验,你认为钉尖朝上和钉尖朝下的可能性一样大吗?你是怎么想的?
由于我们无法保证钉尖和钉帽着地的机会均等,所以钉尖朝上和钉帽朝上的可能性不相等;钉尖朝上的可能性大一点.
(2)小军和小凡一起做了1 000次抛掷图钉的试验,其中有640次钉尖朝上.据此,他们认为钉尖朝上的可能性比钉尖朝下的可能性大,你同意他们的说法吗?
同意.因为做了1 000次试验,试验的次数还是比较多的.在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
师生活动,概率探究
【活动2】
抛掷一枚均匀的硬币,硬币落下后,会出现两种情况:
正面朝上
正面朝下
你认为正面朝上和正面朝下的可能性相同吗?
师生活动,概率探究
【试验操作】
(1)同桌两人做20次掷硬币的游戏,并将数据记录在下表中:
试验总次数
正面朝上的次数
正面朝下的次数
正面朝上的频率
正面朝下的频率
师生活动,概率探究
【试验操作】
(2)累计全班同学的试验结果,并将试验数据汇总填入下表:
试验总次数 20 40 60 80 100 120 140 160 180 200
正面朝上的次数
正面朝上的频率
正面朝下的次数
正面朝下的频率
师生活动,概率探究
【试验操作】
(3)根据上表,完成下面的折线统计图:
(4)观察上面的折线统计图,你发现了什么规律?
当抛掷硬币的次数很大时,正面朝上的频率都会在一个常数0.5附近摆动,即硬币正面朝上的频率具有稳定性.
师生活动,概率探究
【试验操作】
(5)下表列出了一些历史上的数学家所做的抛硬币试验的数据:
表中的数据支持你发现的规律吗?
支持
师生活动,概率探究
【归纳概念】
无论是抛掷质地均匀的硬币还是掷图钉,在试验次数很大时,正面朝上(钉尖朝上)的频率都会在一个常数附近摆动,这就是频率的稳定性.
由于事件A发生的频率表示该事件发生的频繁程度,频率越大,事件A发生越频繁,这就意味着事件A发生
的可能性也越大,因而,我们就用这个常数来表示事件
A发生的可能性的大小.我们把刻画事件A发生的可能性
大小的数值,称为事件A发生的概率,记为P(A).
师生活动,概率探究
【归纳概念】
一般地,大量重复的试验中,我们常用不确定事件A发生的频率来估计事件A发生的概率.
练习:事件A发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少?
必然事件发生的概率是1;不可能事件发生的概率是0;不确定事件A发生的概率P(A)是0与1之间的一个常数.
典例剖析,解决问题
例1 有人说,既然抛掷一枚硬币出现正面的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上,你认为这种说法正
确吗?
这种说法是错误的.抛掷一枚硬币出现正面的概率为0.5,这是大量试验得出的一种规律性结果,对具体的几次试验来讲不一定能体现出这种规律性.在连续抛掷一枚硬币两次的试验中,可能两次均正面向上,也可能两次均反面向上,也可能一次正面向上,一次反面向上.
典例剖析,解决问题
例2 某种油菜籽在相同条件下的发芽试验结果表:
每批粒数n 2 5 10 70 130 310 700 1 500 2 000 3 000
发芽的粒数m 2 4 9 60 116 282 639 1 339 1 806 2 715
发芽的频率m/n 1 0.8 0.9 0.857 0.892 0.910 0.913 0.983 0.903 0.905
则估计油菜籽发芽的概率为____.
0.9
典例剖析,解决问题
例3 某厂打算生产一种中学生使用的笔袋,但无
法确定各种颜色的产量,于是该文具厂就笔袋的颜色随
机调查了5 000名中学生,并在调查到1 000名,2 000名,3 000名,4 000名,5 000名时分别计算了各种颜色的使
用频率,绘制折线图如下:
典例剖析,解决问题
(1)随着调查次数的增加,红色的频率如何变化?
随着调查次数的增加,红色的频率基本稳定在40%左右.
(2)你能估计调查到10 000名同学时,红色的频率是多少吗?
调查到10 000名同学时,红色的频率大约仍是40%.
典例剖析,解决问题
(3)如你是该厂的负责人,你将如何安排生产各种颜色笔袋的产量?
红、黄、蓝、绿以及其他颜色的生产比例大约是
4︰2︰1︰2︰1.
典例剖析,解决问题
【练习】
1.天气预报说下星期一降水概率是90%,下星期三
降水概率是10%,于是有位同学说:下星期一肯定下雨,下星期三肯定不下雨.你认为他说的对吗?
不对.所谓降水概率90%和10%是在大量的统计记录的条件下,那么它是符合大多数同等天气条件下的实际情况,但某些例外情况也是可能发生的.
典例剖析,解决问题
【练习】
2.某运动员进行射击训练,结果如下表所示:
射击次数n 20 100 200 500 800
击中靶心次数m 13 58 104 255 404
击中靶心频率m/n
(1)计算表中的频率.
0.65
0.52
0.58
0.51
0.505
(2)这个射手射击一次,击中靶心的概率是多少?
击中靶心的概率是0.5.
(3)这个射手射击1 600次,击中靶心的次数约是多少?
击中靶心的次数约是800次.
小结与作业
小结
概率是对随机现象的一种数学描述,它可以帮助我们更好地认识随机现象,并对生活中的一些不确定情况作出自己的决策.
从表面上看,随机现象的每一次观察结果都是偶然的,但多次观察某个随机现象,就会发现:在大量的偶然之中存在着必然的规律.
在大量重复进行同一试验时,事件A发生的频率m/n总是接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记为P(A).
小结与作业
小结
一些注意点:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A的概率;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0,因此0≤P(A)≤1.
小结与作业
作业
1.某射击运动员在同一条件下进行射击,结果如下:
射击总次数n 10 20 50 100 200 500 1 000
击中靶心次数m 9 16 41 88 168 429 861
击中靶心频率m/n
(1)完成上表.
(2)根据上表,画出该运动员击中靶心的频率的折线统计图.
(3)观察画出的折线统计图,击中靶心的频率的变化有什么规律?
小结与作业
作业
2.某种麦粒在相同条件下的发芽试验,结果如下:
试验的麦粒数n 100 200 500 1 000 2 000 5 000
发芽的粒数m 94 191 473 954 1 906 4 748
发芽的频率m/n
(1)完成上表;
(2)根据上表,画出麦粒发芽频率的折线统计图;
(3)任取一粒麦粒,估计它能发芽的概率.
小结与作业
作业
3.对某批乒乓球的质量进行随机抽查,结果如下:
随机抽取的乒乓球数n 10 20 50 100 200 500 1 000
优等品数m 7 16 43 81 164 414 825
优等品率m/n
(1)完成上表;
(2)根据上表,在这批乒乓球中任取一个,它为优等品的概率大约是多少?
(3)如果重新再抽取1 000个乒乓球进行质量检查,对比上表记录下数据,两表的结果会一样吗?为什么?
Happy End
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
