6.4一元一次方程的应用(3)--环形跑道上的行程问题
文档属性
| 名称 | 6.4一元一次方程的应用(3)--环形跑道上的行程问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 505.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-12 21:11:20 | ||
图片预览





文档简介
课件13张PPT。环形跑道上的行程问题6.4 一元一次方程的应用(3)一、行程问题的基本数量关系:路程 = 速度 × 时间路程(s)速度(v)时间(t)s = v · t小杰:小丽:同时相向而行,相遇时,
小杰走的路程+小丽走的路程=两人的间距1.相向而行小杰的路程小丽的路程二、直线型行程问题 同时同向而行,追上时,
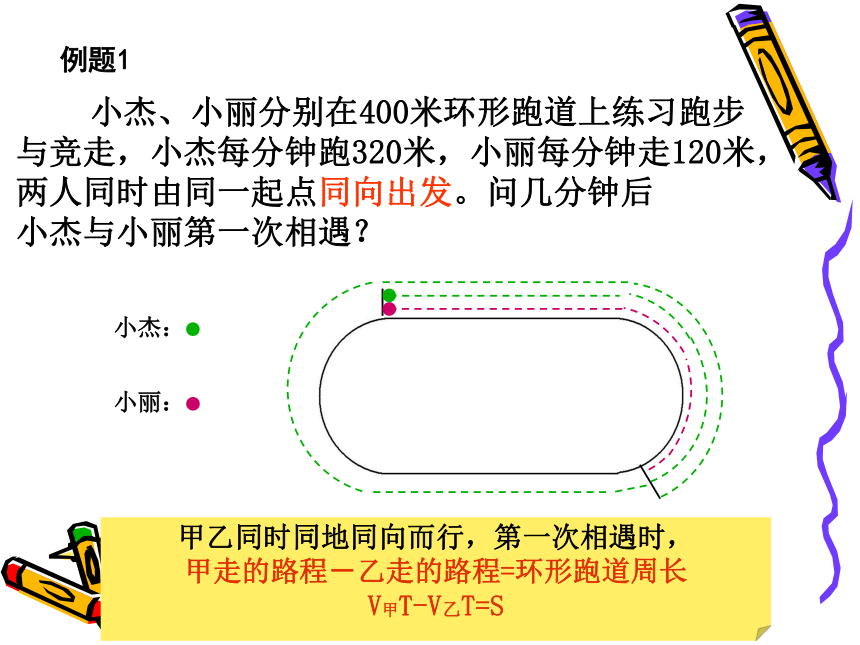
快的人所走路程—慢的人所走路程=两人间距 2.同向而行小杰:小丽:两人间距三、环形跑道行程问题 小杰、小丽分别在400米环形跑道上练习跑步
与竞走,小杰每分钟跑320米,小丽每分钟走120米,
两人同时由同一起点同向出发。问几分钟后
小杰与小丽第一次相遇?
甲乙同时同地同向而行,第一次相遇时,
甲走的路程-乙走的路程=环形跑道周长
V甲T-V乙T=S
小杰:小丽:例题1 小杰、小丽分别在400米的环形跑道上练习跑步与竞走,小杰每分钟跑280米,小丽每分钟走120米,两人同时由同一起点反向出发。问几分钟后小杰与小丽第一次相遇。小杰:小丽:
甲乙同时同地同向而行,第一次相遇时,
甲走的路程+乙走的路程=环形跑道周长
V甲T+V乙T=S
例题2
反向而行:第一次相遇时,甲走的路程+乙走的路程=环形跑道的周长
V甲T+V乙T=S
同向而行:第一次相遇时,甲走的路程-乙走的路程=环形跑道周长
V甲T-V乙T=S
四、小结环形跑道路程 甲、乙两人在一条长400米的环形跑道上跑步,
甲的速度为70米/秒,乙的速度为110米/秒。
(1)若两人同时同地同向跑,几分钟后他们第一次
相遇?
想一想!(2)若两人相距40米,同时反向跑,几分钟后
他们第一次相遇?
两人在环形跑道上跑步 ,两人从同一地点出发,小杰每秒跑3米,小丽每秒跑4米,反向而行,45秒后两人相遇。如果同向而行,几秒后两人再次相遇?甲乙两人绕周长为1000米的环形跑道广场竞走,已知甲每分钟走125米,乙的速度是甲的2倍,现在甲在乙后面250米,乙追上甲需要多少分钟? 解:①小杰第一次追上小丽所需要的时间:200÷(6-4)=100(秒)
②小杰第一次追上小丽时他所跑的路程应为:6×100=600(米)
③小丽第一次被追上时所跑的路程:4×100=400(米)
④小杰第二次追上小丽时所跑的圈数:(600×2)÷200=6(圈)
⑤小丽第2次被追上时所跑的圈数:(400×2)÷200=4(圈)
学校有一条200米长的环形跑道,小杰和小丽同时从起跑线起跑,小杰每秒钟跑6米,小丽每秒钟跑4米,问小杰第一次追上小丽时两人各跑了多少米,第2次追上小丽时两人各跑了多少圈? 六、总结等量关系
是应用题的灵魂!!反向而行:第一次相遇时,甲走的路程+乙走的路程=环形跑道的周长 同向而行:第一次相遇时,甲走的路程-乙走的路程=环形跑道周长
小杰走的路程+小丽走的路程=两人的间距1.相向而行小杰的路程小丽的路程二、直线型行程问题 同时同向而行,追上时,
快的人所走路程—慢的人所走路程=两人间距 2.同向而行小杰:小丽:两人间距三、环形跑道行程问题 小杰、小丽分别在400米环形跑道上练习跑步
与竞走,小杰每分钟跑320米,小丽每分钟走120米,
两人同时由同一起点同向出发。问几分钟后
小杰与小丽第一次相遇?
甲乙同时同地同向而行,第一次相遇时,
甲走的路程-乙走的路程=环形跑道周长
V甲T-V乙T=S
小杰:小丽:例题1 小杰、小丽分别在400米的环形跑道上练习跑步与竞走,小杰每分钟跑280米,小丽每分钟走120米,两人同时由同一起点反向出发。问几分钟后小杰与小丽第一次相遇。小杰:小丽:
甲乙同时同地同向而行,第一次相遇时,
甲走的路程+乙走的路程=环形跑道周长
V甲T+V乙T=S
例题2
反向而行:第一次相遇时,甲走的路程+乙走的路程=环形跑道的周长
V甲T+V乙T=S
同向而行:第一次相遇时,甲走的路程-乙走的路程=环形跑道周长
V甲T-V乙T=S
四、小结环形跑道路程 甲、乙两人在一条长400米的环形跑道上跑步,
甲的速度为70米/秒,乙的速度为110米/秒。
(1)若两人同时同地同向跑,几分钟后他们第一次
相遇?
想一想!(2)若两人相距40米,同时反向跑,几分钟后
他们第一次相遇?
两人在环形跑道上跑步 ,两人从同一地点出发,小杰每秒跑3米,小丽每秒跑4米,反向而行,45秒后两人相遇。如果同向而行,几秒后两人再次相遇?甲乙两人绕周长为1000米的环形跑道广场竞走,已知甲每分钟走125米,乙的速度是甲的2倍,现在甲在乙后面250米,乙追上甲需要多少分钟? 解:①小杰第一次追上小丽所需要的时间:200÷(6-4)=100(秒)
②小杰第一次追上小丽时他所跑的路程应为:6×100=600(米)
③小丽第一次被追上时所跑的路程:4×100=400(米)
④小杰第二次追上小丽时所跑的圈数:(600×2)÷200=6(圈)
⑤小丽第2次被追上时所跑的圈数:(400×2)÷200=4(圈)
学校有一条200米长的环形跑道,小杰和小丽同时从起跑线起跑,小杰每秒钟跑6米,小丽每秒钟跑4米,问小杰第一次追上小丽时两人各跑了多少米,第2次追上小丽时两人各跑了多少圈? 六、总结等量关系
是应用题的灵魂!!反向而行:第一次相遇时,甲走的路程+乙走的路程=环形跑道的周长 同向而行:第一次相遇时,甲走的路程-乙走的路程=环形跑道周长
